Klopt de derde wet van Newton wel?

Afbeelding 1. Een sprong op de maan.Als je vanuit een landingsvoertuig op de maan springt, trekt de zwaartekracht aan je. Maar wat is de tegengestelde reactiekracht die er volgens de derde wet van Newton moet zijn? Foto: NASA / Neil Armstrong.

Verwarring

Volgens de derde wet van Newton hoort bij iedere kracht een even grote, tegengestelde reactiekracht. Stel: ik sta op de grond. Wat is de reactiekracht die hoort bij de zwaartekracht die op mij werkt? Velen denken: de normaalkracht van de grond op mij. Die is immers even groot en tegengesteld gericht.

Nu spring ik van de duikplank in een zwembad. Tijdens mijn val werkt de zwaartekracht op mij. Wat is de bijbehorende reactiekracht? Dat kan nu niet zo’n contactkracht als in het vorige geval zijn. Een veel voorkomend antwoord is: de wrijvingskracht.

Maar nu spring ik uit mijn landingsvoertuig op de maan. Tijdens mijn val werkt de zwaartekracht op mij. Wat is de bijbehorende reactiekracht? Ik spring vrijwel in een vacuum, dus de wrijvingskracht zal het wel niet zijn. Sommigen zeggen: nu geldt de derde wet van Newton niet!

Verlichting

Uiteraard willen we iets fundamenteels als de derde det van Newton niet zo gemakkelijk opgeven. Zelfs in het tweede geval (de val in het zwembad) is duidelijk dat de wrijvingskracht niet de gevraagde reactiekracht kan zijn. Die wrijvingskracht is immers kleiner dan de zwaartekracht!

De oplossing van alle drie problemen is eenvoudig: de reactiekracht bij een kracht die A uitoefent op B, is een kracht die B uitoefent op A. In het eerste geval luidt de vraag dus: Wat is de A die op mij, B, die zwaartekracht uitoefent? Antwoord: dat is de aarde. Volgens de zwaartekrachtswet trek ik even hard aan de aarde als de aarde aan mij trekt. Door zijn veel grotere massa (traagheid) is de aarde echter minder onder de indruk van een kracht van 700 Newton dan mijn persoontje. Hoe dan ook, de kracht waarmee ik aan de aarde trek, is de bijbehorende reactiekracht. Die is er ook tijdens de val in het zwembad. Bij de val op de maan is de gevraagde reactiekracht de kracht die ik op de maan uitoefen.

De elektromagnetische kracht

De derde wet zit al ingebakken in de zwaartekrachtswet van Newton: twee massa’s, m₁ en m₂, oefenen een even grote, maar tegengesteld gerichte zwaartekracht F_z op elkaar uit, met grootte

F_z = G m₁ m₂  / r²,

waarbij r de afstand tussen de massa’s is, en G de zwaartekrachtsconstante van Newton. Op dezelfde manier zit de derde wet ingebakken in de wet van Coulomb, die elektrische krachten beschrijft. Maar bij de magnetische Lorentzkracht F_L,

F_L = q v × B,

waarin B de sterkte van een magneetveld is, en q en v de lading en snelheid van een door dat magneetveld bewegend deeltje, gaat iets mis…

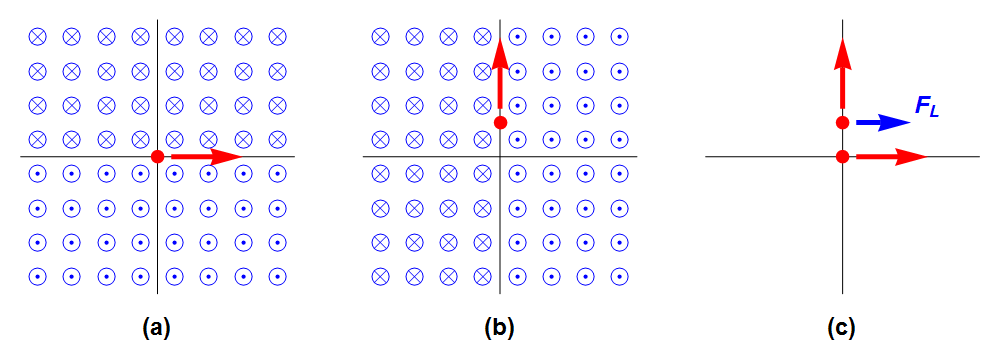
Afbeelding 2. Lorentzkracht tussen twee bewegende deeltjes.(a) Deeltje 1 beweegt langs de x-as. Boven de x-as is het magnetisch veld het papier in gericht; onder de as eruit. Langs de as is het veld nul. (b) De situatie voor deeltje 2, dat langs de y-as beweegt. Nu is het magnetisch veld op die as nul. (c) Beide deeltjes samen. Deeltje 2 ondervindt wel een lorentzkracht van het magnetisch veld van deeltje 1, maar deeltje 1 ondervindt geen lorentzkracht.

Stel: je hebt twee geladen deeltjes, bijvoorbeeld elektronen, die zich door de ruimte bewegen – zie afbeelding 2 hierboven. Die ruimte is verder leeg. Stel verder dat op tijdstip t = 0 deeltje 1 zich bevindt in de oorsprong, en beweegt in de x-richting. We nemen verder aan dat deeltje 2 zich op dat moment op de y-as bevindt (buiten de oorsprong) en ook langs die y-as beweegt. Het is nu duidelijk dat het magneetveld van deeltje 2 gelijk is aan 0 op de y-as. Omdat deeltje 1 zich op t = 0 op de y-as bevindt, oefent deeltje 2 geen magnetische kracht uit op deeltje 1. Het magneetveld van deeltje 1 verdwijnt weliswaar op de x-as, maar niet op de locatie van deeltje 2. Daar staat het magneetveld van deeltje 1 loodrecht op het xy-vlak en dus ook loodrecht op de snelheid van deeltje 2, die langs de y-as is gericht. Kortom, volgens F = q v × B oefent deeltje 1 een Lorentzkracht uit op deeltje 2 die ongelijk is aan de Lorentzkracht van deelt 2 op deeltje 1! De laatste kracht is 0, terwijl de eerste kracht niet 0 is.

Het lijkt alweer alsof de derde wet van Newton niet geldt. Dit probleem lijkt een serieus probleem.

De oplossing

Waarom zouden we moeten geloven in de derde wet van Newton? Omdat we geloven in de translatiesymmetrie van de natuurwetten! Als we alles in het universum 1 meter opschuiven in dezelfde richting, verandert er niets. Emmy Noether heeft ons geleerd dat dergelijke symmetrieën behoudswetten impliceren. De behoudswet die volgt uit de translatiesymmetrie is behoud van impuls. (Analoog volgt bijvoorbeeld energiebehoud uit invariantie van de natuurwetten in de tijd.)

Als de twee geladen deeltjes uit de vorige paragraaf het hele verhaal zouden zijn, dan hadden we een groot probleem. Impuls zou dan niet behouden zijn en daaruit zou dan volgen dat de wetten die elektromagnetisme beschrijven niet translatie-invariant zouden zijn! Onacceptabel!

Blijkbaar is er dus meer dan alleen die twee geladen deeltjes, en blijkbaar kan dat ‘meer’ impuls dragen. Het ‘meer’ blijkt het elektromagnetische veld te zijn. Dat elektromagnetische veld draagt inderdaad impuls en energie, waardoor bijvoorbeeld radiogolven elektronen in de antenne van mijn radio kunnen laten bewegen.

En nu blijkt alles weer te kloppen: als je de totale impuls berekent van deeltje 1 plus deeltje 2 plus het elektromagnetische veld, dan is deze behouden!

Een nieuw probleem

Terug naar de zwaartekracht. Met Newtoniaanse zwaartekracht hebben we geen zwaartekrachtsveld nodig om de derde wet van Newton te redden, zoals wel het geval is bij elektromagnetisme. Toch kun je je afvragen of er een zwaartekrachtsveld bestaat, en of dat impuls en energie bevat. En wat er verandert als je van de Newtoniaanse theorie naar de zwaartekrachtstheorie van Einstein gaat: de algemene relativiteitstheorie. En wat dat dan bijvoorbeeld betekent voor de zwaartekrachtsgolven die sinds kort gedetecteerd kunnen worden… Erg interessante vragen allemaal, waarover we het zeker in een volgend artikel nog eens zullen hebben!

Bronnen:

• David Griffiths, ‘Electromagnetism’ (ISBN 978-0321856562)
• Herbert Goldstein, ‘Classical Mechanics’ (ISBN 978-0201657029)