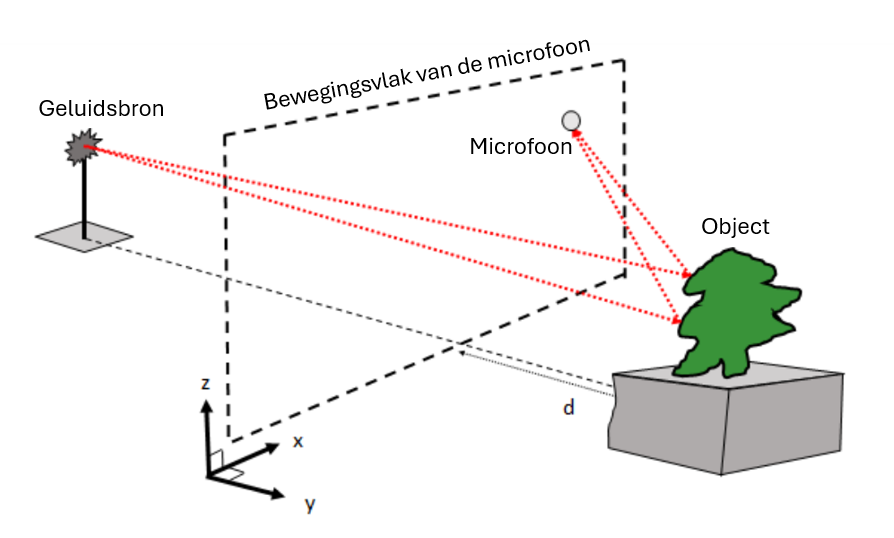
De meetopstelling
Afbeelding 1 toont de meetopstelling tijdens het experiment. Een geluidsbron maakt een geluid, waardoor geluidsgolven in de richting van het te meten object bewegen. Het object weerkaatst de geluidsgolven in allerlei richtingen, die afhankelijk zijn van de vorm van het object. De microfoon beweegt in een vlak tussen de geluidsbron en het object en vangt het weerkaatste geluid op. De tijd t die het duurt voordat de geluidsgolven de microfoon bereiken is afhankelijk van de positie van de microfoon én van de positie van het object. Als bijvoorbeeld de afstand d tussen het object en het bewegingsvlak van de microfoon groter wordt, zal de tijd t groter zijn. Anderzijds is de tijd t groter als de microfoon zich helemaal in de hoek van het bewegingsvlak bevindt. Het kan natuurlijk ook zo zijn dat de microfoon geen signaal oppikt. Dit is bijvoorbeeld het geval als er helemaal geen object staat, waardoor er geen weerkaatsing is.
In afbeelding 2 staat de kerstboom die ik heb gefotografeerd afgebeeld met en zonder kerstballen (dat wil zeggen: met en zonder erop geplakte euromunten). Om de locatie en vorm van de kerstboom nauwkeurig te bepalen is het belangrijk dat de boom enigszins plat is. Een normale kerstboom zal bijvoorbeeld voor weerkaatsing in haast alle mogelijke richtingen zorgen, inclusief allerlei richtingen achter de boom. Geluid in deze richtingen wordt niet opgevangen door de microfoon, die zich maar in een betrekkelijk klein vlak beweegt en alleen teruggekaatste geluidsgolven kan waarnemen, zoals ook zichtbaar in afbeelding 1. Bij het meten van zo’n normale kerstboom zou met bovenstaande meetopstelling dus veel informatie verloren gaan, waardoor de afbeelding van de kerstboom onnauwkeurig wordt.

Van geluidsgolven naar positie
Met behulp van de meetopstelling hebben we in het (x,z)-vlak, zoals aangegeven in afbeelding 1, de intensiteit van de weerkaatste geluidsgolven gemeten als functie van de tijd. Met deze data willen we onze kerstboom afbeelden. Door wat slimme wiskunde toe te passen1, kan achterhaald worden op welke afstand van de bron de verschillende oppervlaktes van de kerstboom zich bevinden. Tijdens het practicum hoef je deze wiskunde niet helemaal zelf te bedenken, maar word je gewezen op de nuttige bronnen en technieken. Met behulp van wat eerste- en tweedejaars wiskundevakken uit de natuurkundebachelor ben je dan al in staat om de technieken toe te passen en in een programmeertaal op te schrijven, zodat je de data kan analyseren. Het resultaat van deze data-analyse is een verzameling van driedimensionale coördinaten (x,y,z) die aangeven waar de oppervlakte van de kerstboom zich bevindt. Met deze resultaten kan de kerstboom afgebeeld worden.
[1] Voor de wiskundigere lezer: we gebruiken o.a. een Fouriertransformatie en zogeheten golffunctie-extrapolatie.
Plakjes boom
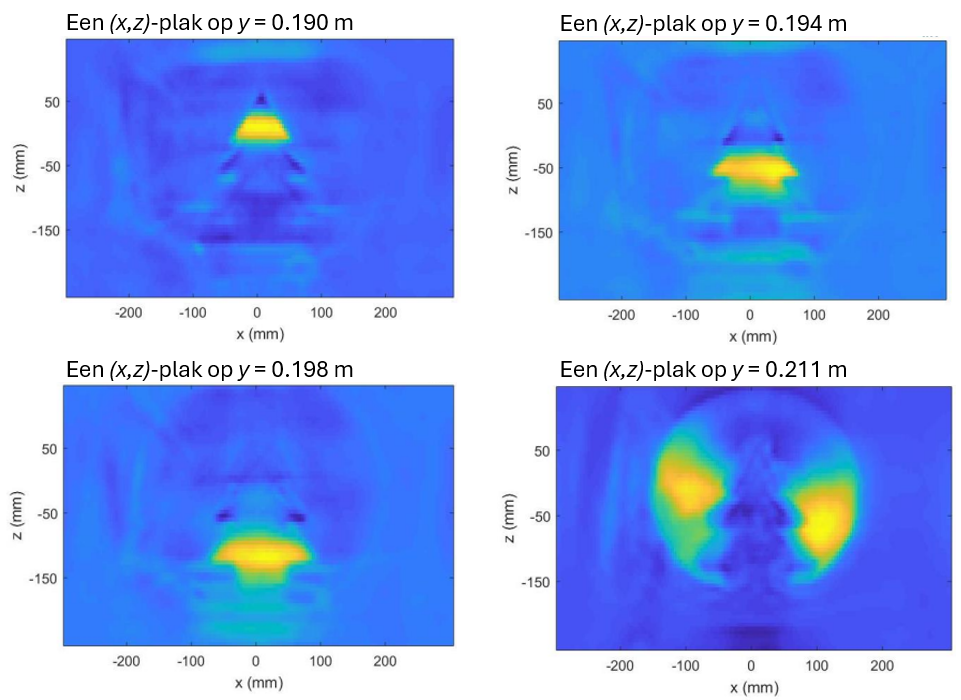
De kerstboom kan zowel in twee als in drie dimensies weergegeven worden. Voor een tweedimensionale afbeelding kies je een y-coördinaat en beeld je de bijbehorende data af in het (x,z)-vlak. Zo geef je als het ware een plakje van de boom weer. Ik laat de 2D-resultaten zien in afbeelding 3, voor verschillende waardes van y. De gele kleur geeft aan dat er vanaf die positie veel geluid weerkaatst is, oftewel, dat zich daar een oppervlakte bevindt. De afbeeldingen laten zien dat de kerstboom iets naar voren helde: voor y = 0,190 m licht de bovenkant van de kerstboom op; pas 8 millimeter verder weg, op y = 0,198 m licht de onderkant van de kerstboom echter op.
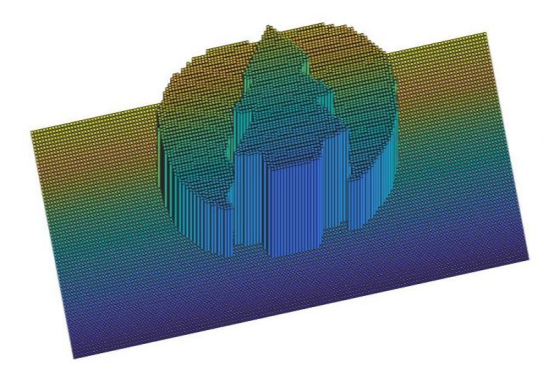
Door alle plakjes in één figuur op elkaar te stapelen is het ook mogelijk om een 3D-afbeelding van de kerstboom te vormen, zoals in afbeelding 4. Deze afbeelding laat zien dat we echt de hele kerstboom hebben gefotografeerd!
De ballen worden gehoord
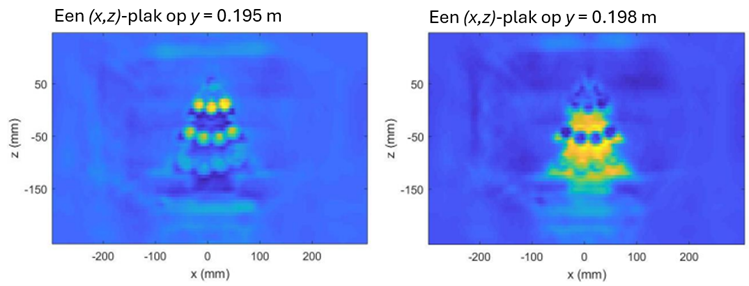
Toen we de kerstboom mét muntjes gingen fotograferen, hebben we de boom iets rechter gezet. Hierdoor bevond zich op positie y = 0,198 m vrijwel de hele oppervlakte van de boom, behalve… op de plekken waar kerstballen zaten! Euromunten hebben een dikte van 2 tot 3 millimeter. De oppervlakte van de kerstballen bevindt zich dus zo’n 2 tot 3 millimeter voor de oppervlakte van de kerstboom. Als de kerstboom oplicht op y = 0,198 m, zouden de munten moeten oplichten rond y = 0,195 m. Dit is precies het resultaat zoals zichtbaar is in afbeelding 5. We kunnen dus inderdaad de kerstballen aan de kerstboom horen!
Dit was het laatste artikel van 2024. Op dinsdag 24, vrijdag 27 en dinsdag 31 december verschijnt het Quantum Universe Jaaroverzicht op onze site; in 2025 zijn we natuurlijk weer terug met de vertrouwde artikelen op dinsdagen en vrijdagen. Fijne feestdagen!