In het eerste deel van deze serie zagen we hoe Alexander Grothendieck de concepten van negatieve getallen en het van elkaar aftrekken van twee getallen generaliseerde. Hij groepeerde getallen in paren – bijvoorbeeld (2,4) – en zag in dat je zo’n paar kunt beschouwen als een abstracte weergave van het getal ‘2-4’, dus min twee. Door alle paren die hetzelfde getal weergeven te groeperen – (3,5) hoort bijvoorbeeld ook in de categorie ‘min twee’ – ontstaat een structuur waarin je met alleen maar ouderwets optellen en met alleen maar positieve getallen, ook aftrekken en negatieve getallen kunt beschrijven. De conclusie: als je objecten eenmaal kunt optellen, ontstaat er vanzelf een unieke manier om ze ook van elkaar af te trekken.
Dat klinkt abstract, zeker omdat de ‘objecten’ uit die laatste zin niet per sé getallen hoeven te zijn – Grothendiecks belangrijkste inzicht was juist dat je de bovenstaande constructie kunt toepassen op alles wat je kunt optellen. In het tweede deel van deze serie beschreef ik een ander voorbeeld van objecten die je kunt optellen: vectorbundels. Zo’n vectorbundel is een meetkundige constructie die op elk punt van de ruimte een ‘extra ruimte’ van vectoren plaatst. Het eenvoudigste voorbeeld zie je in afbeelding 1: de ‘ruimte’ is daar een cirkel, en de ‘extra ruimte’ is een lijn; uit deze bouwstenen kan op twee verschillende manieren een vectorbundel gevormd worden. In onze echte wereld is de ruimte zelf natuurlijk driedimensionaal (of vierdimensionaal als we ook de tijd nog meetellen), en worden plaatjes met nóg meer extra dimensies dus lastig te tekenen – maar het onderliggende wiskundige idee blijft precies hetzelfde.
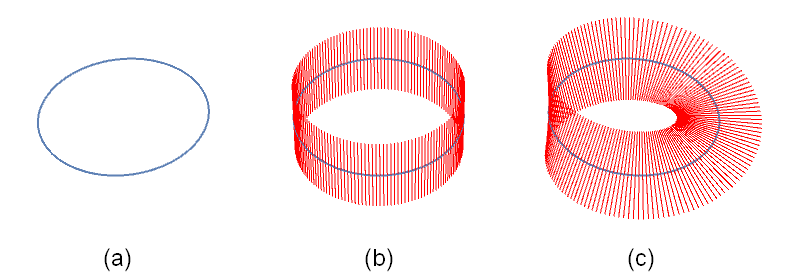
Afbeelding 1. Lijnbundels op een cirkelvormige ruimte.(a) De cirkel is een eenvoudig voorbeeld van een (ééndimensionale) ruimte. (b) De eenvoudigste lijnbundel op de cirkel is de cilinder. (c) Ook de möbiusband kunnen we zien als een lijnbundel op de cirkel.
Uiteindelijk beschreef ik in deel 2 ook waar constructies als deze goed voor zijn: vectorbundels kun je zien als een soort ‘getwist grafiekpapier’, en de grafieken die je op dit papier kunt tekenen kun je zien als de quantummechanische weergave (een soort gegeneraliseerde golffunctie) van deeltjes met ladingen.
Ladingen tellen
Daarbij komt dus de eerste natuurkunde in dit tot nu toe vrij abstracte wiskundige verhaal om de hoek kijken – maar wat heeft de natuurkunde van geladen deeltjes nu te maken met de Grothendieck-constructie waar we deze serie mee begonnen? Een eerste hint voor het antwoord ligt in het feit dat we in de natuurkunde al gewend zijn aan het feit dat je lading kunt tellen. Waar veel natuurkundige grootheden in continu varieerbare hoeveelheden voor kunnen komen – een afstand kan 3 meter zijn, maar ook 3,1 meter of 3,178368212… meter – komt lading in het algemeen alleen voor in discrete hoeveelheden: elektrische lading komt onder normale omstandigheden alleen voor in veelvouden van de lading van het elektron1, e. Iets kan een lading van 2 × e hebben, of 3 × e, of 176 × e, maar niet 1,28 × e.
Negatieve veelvouden van de elektronlading komen natuurlijk ook voor. Een proton heeft bijvoorbeeld een lading die exact tegengesteld is aan de lading van het elektron: als we de twee bij elkaar brengen ontstaat een waterstofatoom dat netto elektrische lading nul heeft. Een historisch ongelukkig feit is overigens dat men er ooit voor gekozen heeft de elektronlading ‘negatief’ te noemen en de protonlading ‘positief’, hoewel juist die eerste de lading is waar we in de praktijk het meest mee werken. Hoe dan ook, als het om optellen en aftrekken gaat, maakt dit onderscheid natuurlijk niet uit – we zouden net zo goed de elektronlading positief kunnen noemen en de protonlading negatief. Waar het om gaat is dat de twee elkaars tegengestelde zijn, en samen 0 opleveren.
Elektrische lading wordt in ons dagelijks leven dus beschreven met gehele getallen – positief én negatief – en als we zouden willen zouden we de lading van alle objecten om ons heen dus kunnen beschrijven met Grothendiecks constructie. In zekere zin doen we dat ook vaak: als we het bijvoorbeeld hebben over een natrium-ion, zeggen we dat dat dezelfde lading heeft als een proton – één plus-lading. Eigenlijk heeft zo’n ion echter 11 positief geladen protonen en 10 negatief geladen elektronen – we zouden de lading dus ook kunnen opschrijven als (11,10) – precies Grothendiecks manier om ‘+1’ weer te geven!

Afbeelding 2. Keukenzout.Keukenzout – natriumchloride – bestaat uit natrium- en chloor-ionen. Als we het natrium vervangen door bijvoorbeeld kalium-ionen, met dezelfde lading, ontstaat een heel ander zout. Afbeelding: onefox.
Deeltjes en antideeltjes
Nu voelt in het voorbeeld van ionen Grothendiecks constructie misschien nog wat onjuist aan – op dezelfde manier als hierboven zouden we een kalium-ion, ook met één positieve ladingseenheid, bijvoorbeeld kunnen schrijven als (19,18); dat ion heeft namelijk 19 protonen en 18 elektronen. In Grothendiecks constructie zit (19,18) in dezelfde klasse als (11,10) – het verschil is in beide gevallen één – en daarmee wordt het kalium-ion dus ‘geïdentificeerd’ met het natrium-ion. Heel logisch als we het over lading hebben, maar misschien een abstractie te ver als het om allerlei andere eigenschappen gaat: in termen van bijvoorbeeld massa is het kalium-ion immers duidelijk verschillend van het natrium-ion.
Er is een andere situatie in de natuur waarin Grothendiecks constructie meer op zijn plaats is: die van deeltjes en anti-deeltjes. Voor elk deeltje dat we kennen bestaat er zo’n anti-deeltje: een ‘tegengesteld’ deeltje waarvan alle eigenschappen, behalve de massa, tegengesteld zijn aan die van het ‘gewone’ deeltje. Zo heeft het elektron bijvoorbeeld als anti-deeltje het positron; een deeltje dat in het bijzonder de tegengestelde lading heeft. Brengen we een elektron en een positron bij elkaar, dan blijft er – op wat energie na die in de vorm van een lichtflits wordt afgevoerd – helemaal niets over. Een elektron en een positron heffen elkaar dus in zekere zin volledig op – en hetzelfde geldt natuurlijk als we twee elektronen en twee positronen bij elkaar brengen, of zeventien elektronen en zeventien positronen.
Voor het ‘tellen’ van de lading van deeltje-antideeltje-combinaties is de constructie van Grothendieck dus ideaal: 1 positron en 2 elektronen leveren precies hetzelfde eindresultaat op als 14 positronen en 15 elektronen, of als één enkel elektron. In Grothendieck-termen: (1,2) behoort tot exact dezelfde klasse als (14,15) en (0,1): de klasse die het eindresultaat ‘één elektron’ (met lading -1) beschrijft.
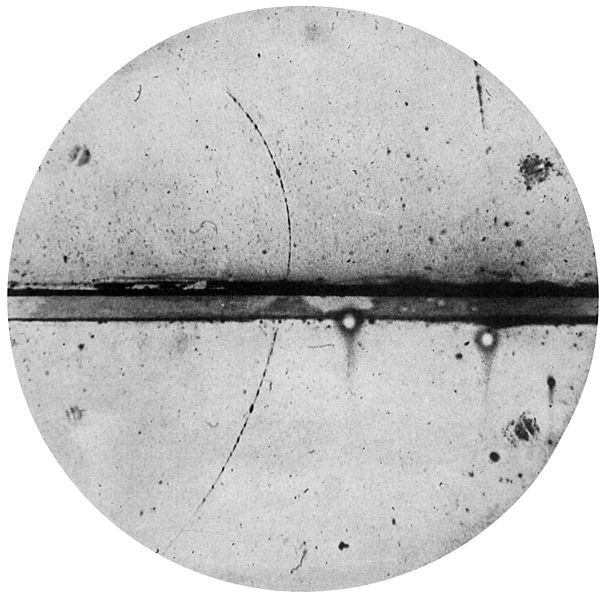
Afbeelding 3. Een positron.Het positron werd in 1932 ontdekt door Carl David Anderson, aan de hand van foto’s als deze, waarop het ’tegendeeltje’ van het elektron in de detector de ‘verkeerde kant’ op beweegt – het elektron zou een soortgelijke bocht de andere kant op maken.
Allemaal leuk en aardig, maar het klinkt nog steeds een beetje alsof we met een wiskundig kanon op een natuurkundige mug aan het schieten zijn. Levert het gebruik van Grothendiecks constructie ook echt nog iets nieuws op, of is het alleen een heel moeilijke manier om deeltjes en antideeltjes te beschrijven? Dat de wiskunde ons wel degelijk iets nieuws kan leren, blijkt als we nu naar hetzelfde probleem gaan kijken, maar dan in de snaartheorie.
D-branen
Over snaartheorie schreven we op deze website al eens een uitgebreide artikelenserie. De belangrijkste aanname in deze theorie is dat de fundamentele bouwstenen waaruit alles om ons heen bestaat niet noodzakelijkerwijs puntvormige deeltjes hoeven te zijn – dat die bouwstenen ook meer dimensies kunnen hebben en bijvoorbeeld de vorm van kleine trillende snaartjes kunnen aannemen. Eéndimensionale objecten, dus, en méér dimensies zijn ook mogelijk. Dan spreken we van D-branen: D2-branen zijn trillende membranen, D3-branen zijn trillende driedimensionale objecten, enzovoort. Enzovoort? Ja, want snaartheorie is maar liefst een tiendimensionale theorie – negen ruimtedimensies en één tijddimensie – en dus kunnen we in die theorie ook D4- tot en met D9-branen beschrijven. (Waarom we al die extra dimensies in het dagelijks leven niet om ons heen zien wordt uitgelegd in dit artikel.)
Allerlei soorten deeltjes dus, met allerlei verschillende aantallen dimensies. Wat dit geheel nu zo mooi aan ons verhaal tot nu toe koppelt, zijn twee feiten: (1) al deze D-branen zijn ook geladen deeltjes, en (2) al deze D-branen kennen ook weer anti-deeltjes. Zoals we in artikel 2 zagen, wil het feit dat D-branen geladen zijn, zeggen dat we ze kunnen beschrijven met behulp van vectorbundels. En zoals we eerder in dit artikel zagen, wil het feit dat er ook anti-D-branen bestaan, zeggen dat Grothendiecks constructie wel eens een mooie manier kan zijn om dit geheel van bouwstenen te beschrijven. We willen Grothendiecks constructie nu dus toepassen op vectorbundels – en laat die combinatie al uitgebreid door wiskundigen bestudeerd zijn! Er is zelfs een mooie naam voor: K-theorie.
K-theorie
Grothendiecks constructie is in feite niet meer dan ‘tellen voor gevorderden’. Maar wat willen we nu precies tellen? Puntdeeltjes, snaren, membranen, andere D-branen? Het mooie is: het blijkt voldoende te zijn om de beginnen met de grootste D-branen die er bestaan: D9-branen, dus – ‘membranen’ die de hele tiendimensionale ruimtetijd vullen. Naïef gezien zouden we nu misschien verwachten dat het ‘tellen’ van D9-branen net zo gaat als dat van elektronen en positronen. We kunnen er 0, 1, 2, 3, enzovoort hebben, en als we de anti-D9-branen als ‘min-branen’ tellen, kunnen er ook -1, -2, -3 enzovoort zijn. Maar zo eenvoudig is het niet! De reden is dat de D-branen zoals gezegd met vectorbundels beschreven worden, en dat er voor elk aantal dimensies meerdere vectorbundels mogelijk zijn.
Laten we voor het gemak eerst weer eens kijken naar de eenvoudigst mogelijke ‘ruimte’: een ééndimensionale cirkel. In het vorige artikel zagen we dat er voor zo’n ruimte twee verschillende vectorbundels mogelijk zijn waarvoor de extra vectorruimte (ook wel de ‘vezel’ genoemd) zelf ook ééndimensionaal is: de cilinder en de möbiusband – zie de afbeelding hieronder. Waar we bij gewone lading dus maar één bouwsteen hebben – de lading van bijvoorbeeld het elektron – zijn er hier zelfs op het eenvoudigste niveau al twéé bouwstenen. Wat gebeurt er nu als we twee van dit soort bouwstenen ‘bij elkaar optellen’? Dan krijgen we vectorbundels waarvan de extra vectorruimte, de vezel dus, tweedimensionaal is. In het geval van de cirkel is dit optellen nogal saai: er blijkt namelijk maar één mogelijke manier te zijn om op elk punt van de cirkel een tweedimensionale vectorruimte toe te voegen. Het resultaat is weer een soort ‘cilinder’, maar dan met op elk punt van de cirkel een vlak in plaats van een lijn toegevoegd –lastig te tekenen omdat we eenvoudigweg niet genoeg dimensies hebben, maar met wat hersengymnastiek wel voor te stellen. Waar het vooral om gaat is dat er dus geen ‘getwiste’ vectorbundels met tweedimensionale vezels zijn, zoals die er in het geval van een eendimensionale vezel wel is – de möbiusband.

Afbeelding 4. Nogmaals: lijnbundels op de cirkel.De cirkel zelf (a) kunnen we ook zien als een vectorbundel, namelijk die met een ‘nuldimensionale vezel’: een punt.
Het maakt voor een cirkelvormige ruimte dus niet uit of we een cilinder bij een cilinder ‘optellen’, of een möbiusband bij een cilinder, of een möbiusband bij een möbiusband – we krijgen altijd precies dezelfde bundel met tweedimensionale vezel. En met meerdimensionale vezels wordt het verhaal niet interessanter: ook voor drie-, vier- en hogerdimensionale vezels bestaat er maar één soort vectorbundel op de cirkel.
Maar wat nu als we de andere kant op gaan? Als we bijvoorbeeld in Grothendiecks constructie een cilinder van een cilinder aftrekken, wat krijgen we dan? Logischerwijs zouden we een vectorbundel verwachten waarvan de vezel nuldimensionaal is. Nuldimensionaal – dat is een punt. We komen dan dus uit bij de cirkel zelf: als je op elk punt van de cirkel één punt zet krijg je… natuurlijk weer precies diezelfde cirkel. We hebben dus een lege ruimte gemaakt, en dat klinkt goed: we hebben namelijk wiskundig beschreven dat een ééndimensionale geladen snaar (die de hele cirkelruimte vult, en beschreven wordt met een lijnbundel) precies opgeheven kan worden door een ééndimensionale anti-snaar (de ‘min’-versie van dezelfde lijnbundel) waarna er een lege ruimte (de cirkel zonder vezel) overblijft.
De oplettende lezer zal nu vragen: wat als we de möbiusband van de cilinder aftrekken? Daar komt het mooie van K-theorie om de hoek kijken! De möbiusband en de cilinder zijn twee verschillende ruimtes, en dus kunnen we het paar
(cilinder, möbiusband)
in Grothendiecks constructie – het paar dat we willen interpreteren als ‘cilinder min möbiusband’ – niet eenvoudigweg identificeren met lege ruimte, in Grothendiecks notatie:
(cirkel, cirkel)
Met andere woorden: een snaar die zo geladen is dat zijn vectorbundel de cilinder is, heft niet zomaar een anti-snaar op als die zo geladen is dat zijn vectorbundel de möbiusband is2. Hoe kunnen we wat er overblijft wel interpreteren? Als volgt: we kunnen proberen de möbiusband ‘glad te strijken’, en er dus zoveel mogelijk een cilinder van te maken. In gedachten kunnen we dat doen door alle vezels ‘rechtop te zetten’, maar dat kan natuurlijk niet rond de hele cirkel – de ‘twist’ blijft immers aanwezig. Het beste wat we kunnen doen is die twist in een zo klein mogelijk gebiedje localiseren, vrijwel in één punt van de cirkel, en verder de möbiusband overal op de cilinder te laten lijken. Het verschil tussen de twee zit ‘m dan dus precies in wat er in de buurt van dat ene punt gebeurt. Kortom: we zouden verwachten dat de snaar en de anti-snaar elkaar bijna overal kunnen opheffen – behalve in (de buurt van) één punt. In dat punt op de cirkel lijkt een puntvormig deeltje achter te blijven!
In de echte, tiendimensionale snaartheorie is dit precies wat er gebeurt. De vectorbundels die D9-branen beschrijven3 kunnen ‘twists’ hebben, en dus leidt het ‘optellen’ en ‘aftrekken’ van deze D9-branen en hun anti-branen niet alleen tot …, -3, -2, -1, 0, 1, 2, 3… D9-branen, maar kunnen er als er evenveel branen als antibranen zijn ook lagerdimensionale D-branen overblijven nadat branen en antibranen elkaar vrijwel opheffen. Het blijkt dat K-theorie op deze manier precies alle mogelijke geladen objecten in de snaartheorie classificeert – Grothendiecks constructie vertelt ons dus exact welke geladen deeltjes er in een bepaalde snaartheorie kunnen voorkomen!
Meer K-theorie
Wat begon als een schijnbaar heel ingewikkelde manier om optellen en aftrekken te definiëren, heeft nu tot een mooi natuurkundig resultaat geleid: het classificeren van alle mogelijke geladen deeltjes in een bepaalde natuurkundige theorie. En dit is nog maar het topje van de ijsberg. K-theorie kan toegepast worden op allerlei andere classificatieproblemen in de natuurkunde. Zo blijkt het in de vaste-stoffysica mogelijk om verschillende mogelijke topologische isolatoren te classificeren met behulp van K-theorie. En er bestaat zelfs iets dat quantum-K-theorie wordt genoemd – hoewel de naam anders suggereert een constructie die in eerste instantie puur wiskundig was, maar die later ook weer toepassingen bleek te hebben in het classificeren van quantummechanische theorieën. Kortom: geen wiskunde zo gek, of er is in de natuurkunde wel een toepassing voor!
[1] Er zijn uitzonderingen op deze regel; quarks hebben bijvoorbeeld elektrische ladingen die veelvouden van een derde van de elektronlading zijn, maar zulke deeltjes komen nooit alléén voor. Verder kunnen we als we willen natuurlijk ook de quarklading beschouwen als de fundamentele lading waar alle andere ladingen veelvouden van zijn.
[2] We spelen hier een klein beetje vals. De lezer zal misschien opmerken dat het paar (cilinder, möbiusband) volgens Grothendiecks constructie in dezelfde klasse moet zitten als (cilinder+cildinder, möbiusband+cilinder), en in dat geval staan links en rechts twee bundels met tweedimensionale vezels – en die zijn allemaal hetzelfde! Het probleem is dat we in onze vereenvoudigde beschrijving gewerkt hebben met vectorbundels met reële vezels, terwijl de K-theorie die in de snaartheorie gebruikt wordt eigenlijk gaat over vectorbundels met complexe vectorruimtes als vezels. In dat geval werkt de constructie die we hier geschetst hebben wel, en blijven er daadwerkelijk lagerdimensionale D-branen over. In ons vereenvoudigde voorbeeld zouden de cilinder en de möbiusband elkaar alsnog opheffen.
[3] D9-branen komen niet in alle soorten snaartheorie voor. We hebben het hier specifiek over de type IIB-snaartheorie, waarin deze objecten wel voorkomen. Voor andere snaartheorieën bestaan er echter soortgelijke constructies, die ook altijd beginnen vanuit de D-branen met de hoogst mogelijke dimensies.