
Afbeelding 1. Een Möbiusband.Voorwerpen met meerdere dimensies kunnen rare kronkels hebben. In deze serie zullen we zien dat zulke vreemde vormen ook in de fundamentele natuurkunde een rol spelen. Afbeelding: Jennifer Smith.
Van positief naar negatief
In het eerste artikel uit dit drieluik hebben we gezien hoe Alexander Grothendieck het begrip ‘negatief getal’ formaliseerde en algemener maakte. Het idee is om te beginnen met alle positieve getallen, en daarvan paren te maken. Een paar (a,b) staat dan model voor het verschil ‘a-b’, en door paren te groeperen kunnen we hele klassen van zulke paren zien als één negatief getal – de klasse waarin (2,4) en (11,13) zitten staat bijvoorbeeld voor het negatieve getal ‘min twee’. Het mooie van deze constructie – lees het vooral nog eens na in het vorige artikel – was dat we op die manier negatieve getallen en het aftrekken van getallen kunnen beschrijven zonder ooit een minteken te gebruiken. Dat wil zeggen: als we maar weten wat positieve getallen en optellen zijn, volgt het begrip van negatieve getallen en aftrekken automatisch.
Wat hebben we in de praktijk nu aan deze nogal kunstmatig ogende constructie? Met negatieve getallen en het aftrekken van getallen zijn we allemaal van kinds af aan bekend, maar er zijn – bijvoorbeeld in de natuurkunde – ook allerlei situaties waar alleen ‘positieve’ begrippen en ‘optellen’ een duidelijke interpretatie hebben. Denk aan dimensies: we kunnen ons prima voorstellen wat iets twee- of driedimensionaals is, en kunnen met wat meer moeite misschien ook nog wel iets zeven- of tiendimensionaals beschrijven, maar wat betekent ‘min vijf-dimensionaal’? Dat lijkt een onzinnige vraag – en toch blijkt het antwoord op die vraag met behulp van Grothendiecks constructie ons iets over de natuur te kunnen vertellen!
Dimensies
Wat is een dimensie eigenlijk? In de meest algemene zin zou je kunnen zeggen: een dimensie is alles wat we met een coördinaat kunnen beschrijven. Denk aan onze eigen wereld: die is driedimensionaal, omdat we elk punt in de wereld met drie coördinaten op een unieke manier kunnen aanduiden: zoveel meter naar links, zoveel meter naar achteren en zoveel meten naar boven – of wiskundiger: x, y en z. Een vel papier (als we de dikte daarvan buiten beschouwing laten) is om dezelfde reden tweedimensionaal: elk punt op het papier kan met alleen een x– en een y-coördinaat beschreven worden.
Méér dan drie dimensies kan natuurlijk ook. Ruimte-achtige extra dimensies zien we om ons heen in de natuur niet, al komen zulke dimensies bijvoorbeeld in de snaartheorie wel voor, en zegt Einsteins relativiteitstheorie dat we ook tijd eigenlijk als een vierde dimensie zouden moeten zien. Maar extra dimensies invoeren kan ook veel eenvoudiger: alles wat met een coördinaat beschreven kan worden, kunnen we immers zien als een dimensie. Laten we eens een eenvoudig voorbeeld bekijken: temperatuur.
Afbeelding 2. Plaats en temperatuur.Temperatuur kan van plek tot plek verschillen. In zekere zin kunnen we temperatuur daarmee zien als een extra coördinaat, en dus als een extra dimensie. Afbeelding: Robert A. Rohde / Berkeley Earth.
Een temperatuur-dimensie?
Elk punt in de kamer waar ik me nu bevind heeft een temperatuur. Die temperatuur is niet overal precies hetzelfde: bij het raam is het wat kouder dan gemiddeld, en in de buurt van het theelichtje dat op tafel staat te branden is het wat warmer. Om een punt in de kamer en zijn temperatuur weer te geven heb ik dus vier coördinaten nodig: x, y, z en T. Zo is (0, 1, 2, 20) het punt bovenop de kast (recht voor mijn neus, een meter naar voren, twee meter boven de vloer en het is daar 20 graden Celsius), is (1, 1, 1.5, 19) een punt vlak voor het raam, en geeft (-1, -1, 1, 60) een punt vlak bij het theelichtje aan.
Door de temperatuur van elk punt in ons verhaal mee te nemen hebben we dus een dimensie toegevoegd! Onze wereld is vier- in plaats van driedimensionaal geworden. Al is het misschien beter om te spreken van ‘(3+1)-dimensionaal’: de nieuwe dimensies is natuurkundig gezien natuurlijk heel anders dan de eerste drie. Zo kunnen we de ruimtelijke dimensies met elkaar ‘mengen’ door simpelweg te draaien: als ik me een kwartslag draai, is de x-dimensie opeens de y-dimensie geworden. Ik kan me aan de andere kant natuurlijk niet zo draaien dan de x-dimensie opeens de T-dimensie wordt. De temperatuur-dimensie is dus duidelijk van andere aard dan de ruimtelijke dimensies, maar wordt net zo goed door een coördinaat beschreven. En ‘bewegen’ in die dimensie kan ook: als ik het theelichtje bijvoorbeeld uitblaas ‘verplaatst’ het theelichtje in de T-richting, van (-1,-1, 1, 60) naar (-1, -1, 1, 20).
Een eerste vectorbundel
Als we de temperatuurdimensie symbolisch willen weergeven, kunnen we dat natuurlijk wel prima met een extra ruimtelijke richting doen. Laten we ons voor het tekengemak een ééndimensionale wereld voorstellen – een lijn, dus. Door nu de temperatuurrichting als een tweede dimensie te tekenen, kunnen we makkelijk voor elk punt in de kamer de temperatuur weergeven – wat we dan doen is niets anders dan een grafiek tekenen. In afbeelding 3 zie je bijvoorbeeld het temperatuurverloop in een eendimensionale kamer met daarin ook een theelichtje (de piek in de grafiek) en een raam (het punt aan de rand van de kamer waar de temperatuur iets lager wordt).
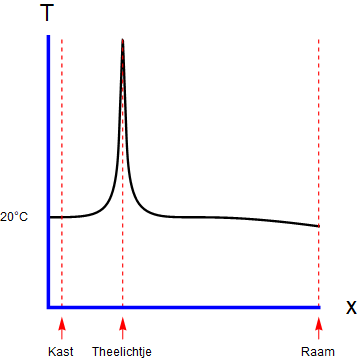
Afbeelding 3. Temperatuur in een ééndimensionale kamer.De kamer kan worden gezien als de x-as; op elk punt in die kamer is er een hele lijn van mogelijke temperaturen. De drie rood gestippelde lijnen geven bijvoorbeeld de mogelijke temperaturen bij de kast, het theelichtje en het raam aan.
Nu beschrijven we in detail wat we in deze constructie hebben gedaan. Aan elk punt in de kamer (een punt in de horizontale richting, weergegeven door een x-coördinaat) hebben we een hele lijn van mogelijke temperaturen toegevoegd (een lijn in de verticale richting, geparametriseerd met een T-coördinaat). We kunnen de tweedimensionale grafiek dus zien als een gigantische verzameling van ‘temperatuurlijnen’; één lijn voor elk punt in onze eendimensionale wereld. In de echte, driedimensionale wereld kunnen we natuurlijk hetzelfde doen: op elk punt in die wereld beschrijven we de temperatuur dan door aan dat punt een lijn van mogelijke temperaturen toe te voegen, en zo ontstaat een vierdimensionaal geheel.
Zo’n gigantische verzameling van lijnen – één voor elk punt – wordt in de wiskunde een lijnbundel genoemd. Maar de lijnbundel die we nu gemaakt hebben is nog maar het begin: het is een voorbeeld van een nog veel algemenere constructie die vectorbundel heet.
Velden en vectorbundels
De constructie hierboven kan op twee manieren algemener gemaakt worden. Ten eerste zijn er natuurlijk grootheden in de natuur die zelf door meer dan één coördinaat beschreven worden. Denk aan een elektrisch veld: zo’n veld heeft, op elk punt in de ruimte, een grootte en een richting. We kunnen het elektrische veld op een bepaald punt – met bijvoorbeeld x-, y– en z-coördinaten (1, 3, 2) – weergeven met nog eens drie coördinaten – het veld kan bijvoorbeeld in de richting (2, -3, 4) wijzen. In totaal geven we het veld op dat punt dan dus weer met 3+3 coördinaten: (1, 3, 2, 2, -3, 4).
Nu hebben we op elk punt van de ruimte dus maar liefst een driedimensionale extra ruimte toegevoegd. Wiskundigen noemen ook deze enorme verzameling van driedimensionale ruimtes een ‘bundel’; in dit algemenere geval spreekt men van een vectorbundel omdat elke toegevoegde ruimte bestaat uit ‘vectoren’ – pijltjes met een grootte en een richting. We kunnen onze eerder geconstrueerde lijnbundel uit het temperatuurvoorbeeld zien als een speciale vectorbundel, waarin de ‘pijltjes’ zelf één- in plaats van driedimensionaal zijn.
Er is nóg een manier waarop we het idee van een vectorbundel kunnen uitbreiden – een manier die misschien natuurkundig niet direct voor de hand ligt, maar wiskundig wat meer. Stel dat we van onze eendimensionale wereld nu eens een cirkel maken. Zie afbeelding 4a: als je in deze wereld dus maar lang genoeg doorloopt kom je weer op hetzelfde punt terug. Nu willen we net als in het temperatuurvoorbeeld op elk punt van deze wereld een lijn toevoegen. Hoe doen we dat? De eenvoudigste oplossing is getekend in afbeelding 4b: we zetten alle lijnen netjes ‘rechtop’, en krijgen zo iets wat op een cilinder lijkt.
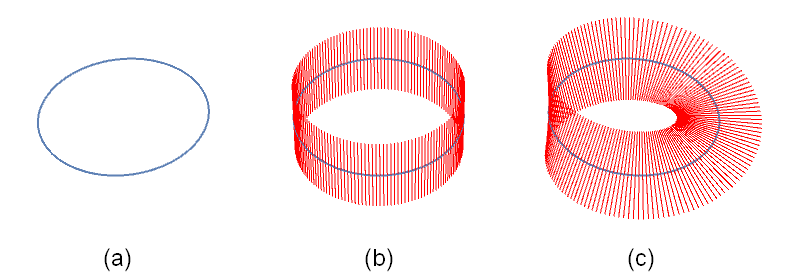
Afbeelding 4. Lijnbundels op een cirkelvormige ruimte.(a) Een cirkelvorminge ruimte. (b) De eenvoudigste manier om op elk punt van de ruimte een lijn toe te voegen: een cilinder. (c) Een andere manier om op elk punt van de ruimte een lijn toe te voegen: een Möbiusband.
Maar wat als we de lijnen wat draaien, en uiteindelijk na een heel rondje om onze wereld heen zó aan elkaar plakken dat de oorspronkelijke lijn ‘op zijn kop staat’? Dan krijg je de situatie uit afbeelding 4c: een figuur die ook wel een Möbiusband wordt genoemd. Ook dit is een lijnbundel – maar wel een andere dan die uit afbeelding 4b! Deze lijnbundels is topologisch anders: we kunnen zonder knippen en plakken de ene bundel niet in de andere vervormen. (Een leuke puzzel: overtuig jezelf ervan dat een lijnbundel waarbij je de lijn in een rondje om de wereld twee keer ronddraait, topologisch gezien hetzelfde is als de cilinder uit afbeelding 4a.)
Goed, de wiskunde geeft ons hier weer een leuke truc, maar zoals altijd is de vraag natuurlijk: komt een dergelijke rare constructie ook in de natuur voor?
‘Getwiste’ velden
Het verrassende antwoord is: ja! De temperatuur en het elektrisch veld zijn natuurlijk niet de enige plaatsafhankelijke grootheden in de natuur. Er zijn heel veel van dat soort grootheden, die we naar analogie met het elektrisch veld ook in het algemeen velden noemen. We kunnen dus spreken van het temperatuurveld, en bekend is bijvoorbeeld ook het magnetische veld. Wat natuurkundigen in de loop der jaren hebben ontdekt, is dat bij elk deeltje en elke kracht op die manier een veld hoort.
Een veld dat een deeltje beschrijft? Hoe moet je je dat voorstellen? Een deeltje bevindt zich toch op één plaats? Het lijkt vreemd om een deeltje dan te beschrijven als iets dat op elke plaats in de ruimte een waarde heeft. Althans, in de klassieke natuurkunde lijkt dat vreemd, maar als we de quantummechanica in ons verhaal meenemen, wordt dat heel anders! Volgens de quantummechanica is een deeltje nooit op één precieze plek – nee, je kunt alleen op elke plek de kans beschrijven dat een deeltje zich daar bevindt. Zo beschrijf je dus zelfs één enkel deeltje door op elke plek in het heelal een getal voor te schrijven – en daarom is het dat ook deeltjes in de quantummechanica zo mooi met velden beschreven kunnen worden.
Maar de natuur heeft nog meer moois in petto: het blijkt dat sommige deeltjes beschreven moeten worden met bundels waarin ‘twists’ zitten – bundels zoals de Möbiusband die we eerder tegenkwamen, dus. Welke deeltjes? Het blijkt dat deze beschrijving nodig is voor deeltjes die geladen zijn – bijvoorbeeld elektrisch geladen, of met ladingen die de sterke of zwakke kernkracht voelen. Voor zulke geladen deeltjes kan het namelijk gebeuren dat je die over een bepaald pad door de wereld heen beweegt, maar dat de configuratie van het deeltje net iets anders is geworden als het deeltje op zijn oorspronkelijke plaats terugkomt. Een voorbeeld van dit verschijnsel is het Aharonov-Bohmeffect – een interessant verschijnsel waar we nog wel eens een apart artikel aan zullen wijden.
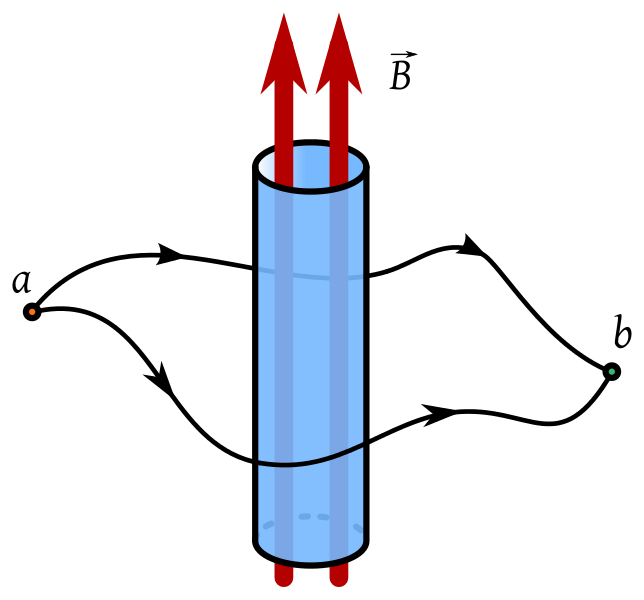
Afbeelding 5. Het Aharonov-Bohmeffect.In het Aharonov-Bohmexperiment wordt door een metalen staaf een magnetisch veld B aangelegd. Wanneer een elektrisch geladen deeltje vervolgens van punt (a) naar punt (b) beweegt is er quantummechanisch een verschil te meten tussen deeltjes die links en rechts om de staaf heen bewogen zijn. Met andere woorden: een deeltje dat van (a) naar (b) beweegt en ‘langs de andere kant’ weer terug naar (a), is niet meer hetzelfde als het eerst was. Het verschil kan wiskundig precies worden gemaakt met behulp van een ‘getwiste’ vectorbundel.
Kortom: geen wiskunde zo gek of er blijkt ergens in de natuurkunde wel een plek voor. Dat geldt voor extra dimensies, die we nodig hebben om velden te beschrijven, en dus ook voor ‘getwiste’ vectorbundels, die we nodig hebben om geladen deeltjes te beschrijven. Maar nu komen we terug bij onze oorspronkelijke vraag. Dimensies kun je tellen: 1-, 2-, 3-, 4-dimensionaal. Je kunt in zekere zin ook dimensies optellen: als ik van elk punt in de ruime de temperatuur en het elektrisch veld wil beschrijven heb ik een vectorbundel nodig die op elk punt 1+3=4 dimensies toevoegt. Nu denken we terug aan de constructie van Grothendieck uit het vorige artikel, en vragen ons af: kunnen we dimensies van vectorbundels ook van elkaar aftrekken, en kunnen we zelfs spreken van vectorbundels met nul dimensies of negatieve dimensies? En als dat wiskundig kan, hebben dan zelfs die bizarre objecten een rol in de natuurkunde?
Het zal je misschien inmiddels niet meer verbazen: ook hier is het antwoord weer ‘ja’. Dat antwoord, dat bekend staat onder de mysterieuze naam K-theorie, beschrijf ik in het laatste deel van deze serie, dat op vrijdag 30 augustus verschijnt.
In de zomerperiode verschijnen de Quantum Universe-artikelen éénmaal per week, op vrijdag. Vanaf september is de redactie weer terug van alle conferenties en vakanties, en verschijnen de artikelen weer tweemaal per week, op dinsdag en vrijdag.