Als je houdt van fietsen, wandelen, of een andere activiteit waar je een afstand voor moet afleggen, zal je misschien bekend zijn met Strava. Strava is een app waarop je je activiteit kunt uploaden en zo de afstand die je hebt afgelegd, samen met de bijbehorende tijd, kunt delen met je volgers, of kunt bijhouden voor jezelf. Voor sommige mensen wordt het een spelletje om een mooi rond getal of een snelle tijd te delen. Voor een wetenschapper geeft het uitvoeren van zo’n fysieke activiteit bovendien een hoop tijd om na te denken, bijvoorbeeld over hoe die tijd en afstand zijn gedefinieerd. Want wat is nou een meter, en hoe weet ik zeker dat mijn meter even lang is als een meter aan de andere kant van de wereld, zoals in Nieuw-Zeeland?
Door de geschiedenis heen werden uiteraard al bepaalde maten gebruikt om de afstand aan te geven, bijvoorbeeld met behulp van ledematen, zoals een voet. Maar de lengte van mijn voet is niet dezelfde als de lengte van de voet van mijn zusje, laat staan als die van een willekeurige persoon in Nieuw-Zeeland. In 1637 stelde Christiaan Huygens een preciezere maat voor, namelijk de lengte van de arm van een slinger die een periode van precies één seconde heeft. De seconde zelf kon in die tijd wel al redelijk precies bepaald worden met astronomische data. Men realiseerde zich echter dat ook deze lengte verschilt afhankelijk van waar je bent op aarde, wat na het werk van Newton enkele tientallen jaren later verklaard kon worden door het feit dat de zwaartekracht niet overal op aarde hetzelfde is. Daarom definieerden de Fransen in 1791, tijdens de Franse Revolutie, de meter. Dit werd als volgt gedaan: de meter is 1/10.000.000ste deel van de afstand van de Noordpool tot de evenaar, gemeten langs de lijn tussen deze twee die door Parijs loopt. Over een periode van zo’n zeven jaar werd de meter gemeten, wat resulteerde in een platina staaf, de mètre étalon, die bewaard werd in Parijs.

Gedurende zo’n 130 jaar vormden de platina staaf, samen met kopieën van deze staaf, de standaarddefinitie van de meter. Heel handig was het niet. Bij een kopie was altijd een bepaalde onzekerheid over hoe precies zij was en bovendien waren er niet veel kopieën beschikbaar. Daarnaast is de precieze lengte van de staaf afhankelijk van de temperatuur. Een nieuwe definitie was gewenst.
Een spectrale definitie
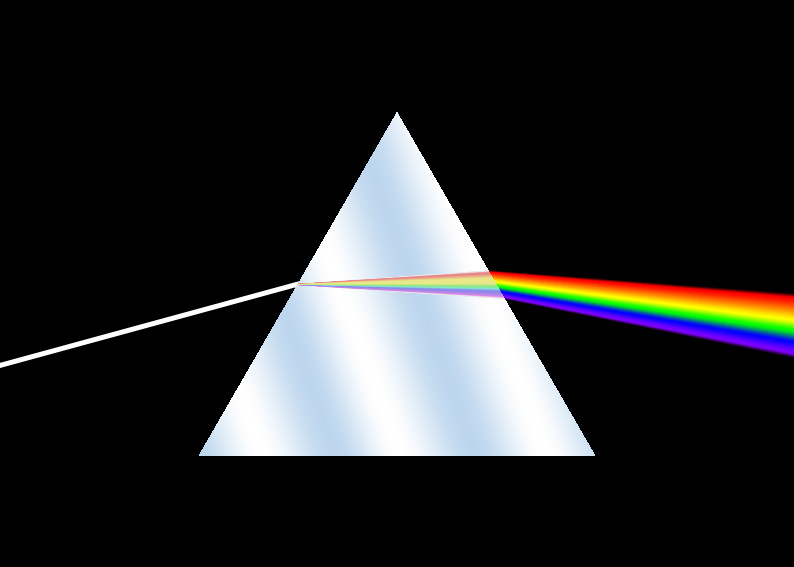
Vooruitgangen in de technologie maakten het mogelijk om de definitie van de meter te verscherpen. Met behulp van interferentiepatronen van energetische cadmiumatomen – het element in het periodiek systeem met atoomnummer 48 – werd de meter in 1927 geherdefinieerd. De nieuwe definitie werd een specifiek aantal golflengtes van het licht dat vrijkomt bij een fotonemissie uit een cadmiumatoom. Zo’n emissie vindt plaats wanneer een elektron van een energetische toestand terugvalt naar een minder energetische toestand, waarbij het een foton uitzendt – een lichtdeeltje, dus. Zo’n foton heeft altijd dezelfde golflengte. In het spectrum van licht – de regenboogachtige ‘waaier’ die je krijgt als je licht bijvoorbeeld door een prisma laat vallen – heet deze golflengte een spectraallijn.
De emissie van cadmium is overal op aarde te herhalen en geeft overal dezelfde uitslag, maar vanwege praktische redenen was de definitie toch niet definitief. In 1960 werd de definitie van de meter veranderd naar een emissie van krypton (atoomnummer 36), omdat dit element beter beschikbaar was in Europa en een hogere precisie haalde in laboratoriummetingen. De definitie van de meter bleef dus spectraal. Hetzelfde principe wordt tegenwoordig nog steeds gehanteerd, zij het in een andere vorm. Metingen van de snelheid van het licht werden namelijk steeds preciezer en betrouwbaarder. Volgens algemene relativiteit is de snelheid van het licht constant, dus in 1983 werd de definitie van een meter veranderd naar de afstand die licht in het vacuüm aflegt in 1/299.792.458ste seconde. Nu is het de seconde die spectraal gedefinieerd is, en wel als de tijd van 9.192.631.770 periodes van het foton dat hoort bij de emissie tussen de (hyperfijne) grondtoestanden van het cesium-133-atoom.
Waarom spectraal?
Misschien ben je je gaan afvragen waarom een spectrale definitie nou een goede definitie is, of misschien heeft het bovenstaande tussenkopje die vraag voor je gesteld. Een deel van de motivatie heb ik al genoemd: overal ter aarde, en zelfs overal in het universum, kan de periode van het foton dat vrijkomt bij een overgang tussen de grondtoestanden van een cesium-133-atoom worden gemeten. Wiskundige technieken waar ik hieronder op terug kom laten zien dat zo’n overgang maar één mogelijke uitkomst heeft. Door de meter dus aan de hand van zo’n overgang te definiëren, weten we zeker dat iedereen dezelfde meter gebruikt! (Een feitje: dit universele gedrag heeft tot de conclusie geleid dat het universum aan het uitdijen is, namelijk door waargenomen verschuivingen in de spectraallijnen die verklaard worden door het dopplereffect!)
Maar wat maakt nou dat overal in het universum dezelfde overgang van cesium-133 wordt gemeten, terwijl dat bij een platina staaf of bij andere voorstellen voor de definitie van de meter niet het geval is? Het antwoord op deze vraag komt in essentie voort uit de quantummechanica. In de klassieke natuurkunde kunnen de positie en de snelheid (of, om precies te zijn, de impuls) van een object tegelijkertijd met willekeurige precisie worden gemeten. In quantummechanica is dit niet meer mogelijk; als we eerst de positie van een object meten en daarna de impuls, geeft dat een ander resultaat dan als we eerst de impuls meten en daarna de positie. In wiskundige termen formuleren we dat als volgt: positie en impuls commuteren niet.
Dit principe heeft nog een andere consequentie: zodra we een grootheid meten die wél commuteert met het meten van de positie, ligt de positie van dat wat we hebben gemeten vervolgens ook tot op zekere hoogte vast. Dit kan in wiskundige termen worden uitgedrukt: als we een grootheid meten die commuteert met het meten van de positie, belanden we in een eigenruimte van de positiemeting. Dit betekent dat, na het meten van die grootheid, de uitkomst van de positiemeting al deels of geheel vastligt, zodat hetgeen we willen meten wordt gelokaliseerd. Dit principe maakt dat de platina staaf noodgedwongen op een bepaalde plek moest zijn, in dit geval in Parijs. Om de meter níét te lokaliseren op een specifieke plaats, is het dus nodig om de meter te definiëren aan de hand van een meting die níét commuteert met de meting van positie, bijvoorbeeld aan de hand van impuls. In zo’n geval moet de definitie van de meter dus wel breder geldig zijn dan op één enkele plaats! Om te zien dat dit precies is wat gebeurt bij de spectrale definitie, hebben we iets meer wiskunde nodig.
Het spectrum van een atoom
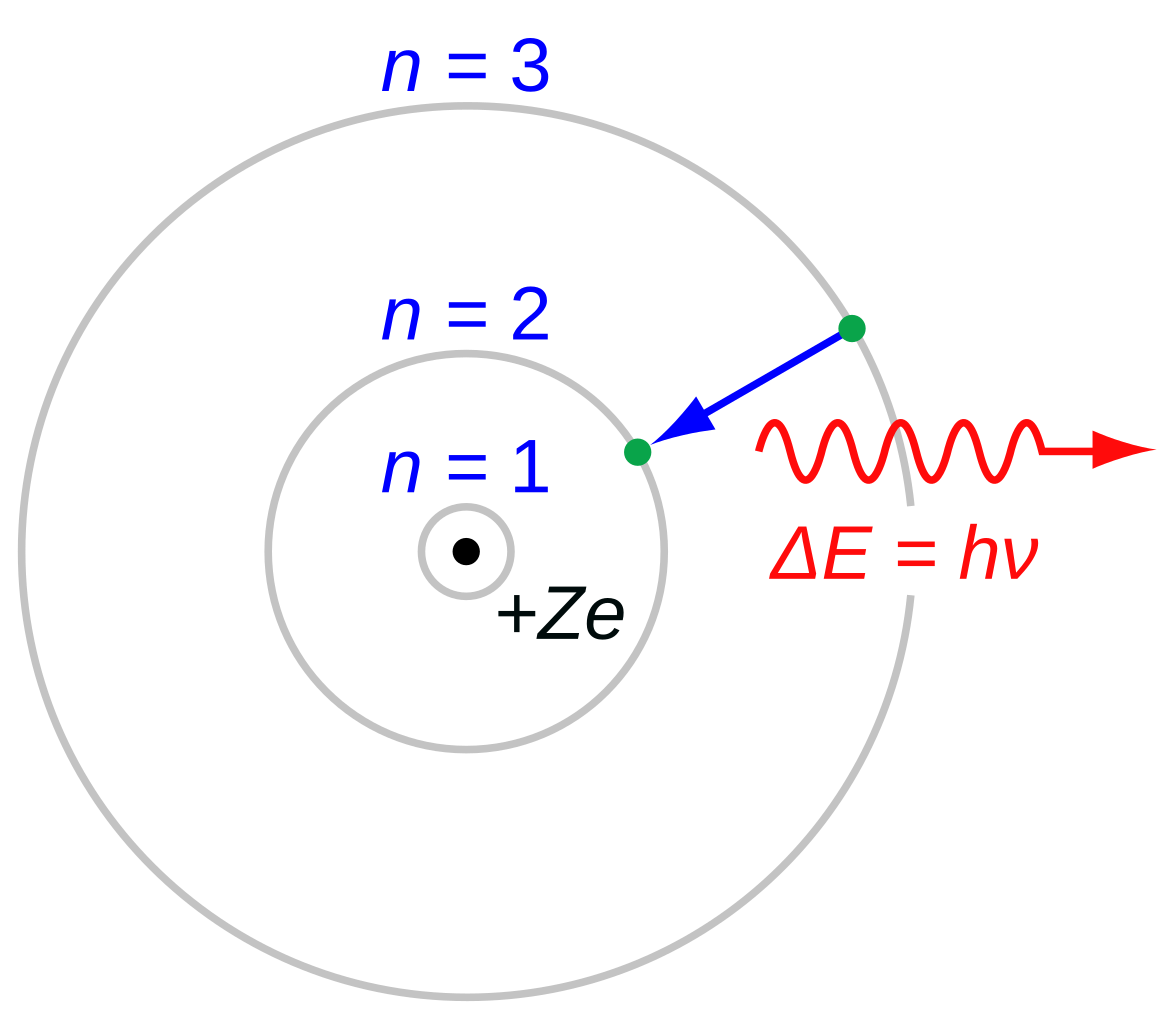
Een algemene formule om de golflengte van spectraallijnen te voorspellen, werd opgeschreven door de Zweed Johannes Rydberg in 1888. In die tijd was quantummechanica nog niet ontdekt en was de gevestigde natuurkunde niet geschikt om de golflengtes theoretisch uit te rekenen. De formule was dus puur gebaseerd op beschikbare data uit experimenten. Zo’n 25 jaar later, in 1913, werd de formule theoretisch afgeleid door de Deense natuurkundige Niels Bohr, gebruikmakend van een primitieve vorm van quantummechanica. De afleiding van de formule maakte gebruik van Bohrs model van het atoom, waarbij elektronen in stabiele banen (ook wel schillen genoemd) rondom de kern van een atoom bewegen. Die schillen zijn genummerd en bevinden zich op vaste afstand vanaf de kern, zoals weergeven in afbeelding 2. Tegenwoordig weten we dat dit model niet klopt, maar het is alsnog handig om bepaalde resultaten, zoals de formule van Rydberg, inzichtelijk te maken. Voor het waterstofatoom luidt de formule van Rydberg als volgt:
\( \frac{1}{\lambda_\text{vac}}=R_H \left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right). \)
Hier is \( \lambda_{\text{vac}} \) de golflengte van het foton in vacuüm, \( R_H \) een voor waterstof constante factor die de constante van Rydberg wordt genoemd, \( n_1 \) het gehele getal dat het energieniveau labelt waar het elektron naar terugvalt en \( n_2 \) eenzelfde getal voor het energieniveau waar het elektron vandaan valt. De empirische data waarop Rydberg zijn formule baseerde, kwamen van het spectrum van verscheidene metalen uit het periodiek systeem, waar het hem opviel dat de golflengtes in bepaalde reeksen kwamen. Door dit te vergelijken met de formule van Balmer voor een reeks spectraallijnen in het spectrum van waterstof, kwam hij tot zijn formule.
Rydbergs formule was echter nog niet exact. Met de huidige kennis viel dat te verwachten, omdat het atoommodel van Bohr niet helemaal klopte, en ook omdat uit empirische data de formule niet blijkt te kloppen: in de spectraallijnen zijn verscheidene soorten splitsingen die niet te verklaren zijn met behulp van het atoommodel van Bohr.
Twee soorten splitsingen in de spectraallijnen zijn de hyperfijnstructuur en de fijnstructuur, die, respectievelijk, beschreven kunnen worden met de Schrödingervergelijking en de Diracvergelijking. De splitsingen zitten tussen energieniveaus van elektronen die zich, in het atoommodel van Bohr, in dezelfde schil bevinden. Deze elektronen zijn niet allemaal hetzelfde vanwege het uitsluitingsprincipe van Pauli: in één schil zitten elektronen met verschillende spin en impulsmoment. Dit zorgt voor de fijnstructuur. De hyperfijnstructuur daarentegen wordt veroorzaakt door magnetische velden die ontstaan doordat de kern en de elektronen in de schillen elektrisch geladen zijn.
De golflengte waarmee de seconde is gedefinieerd, komt van een foton dat wordt uitgezonden bij een hyperfijne overgang in het cesium-133-atoom. Desondanks zullen we nu kort de Diracvergelijking bekijken in plaats van de Schrödingervergelijking – waarom we dat doen wordt zo direct duidelijk. De Diracvergelijking (al eerder ter sprake gekomen in dit artikel) verenigt quantummechanica met speciale relativiteit. Dat wil zeggen: de vergelijking beschrijft zowel het heel kleine als het heel snelle. In haar originele vorm ziet de Diracvergelijking er als volgt uit:
\( (c\alpha\cdot\hat{p}+\beta m c^2)\psi=i\hbar\frac{\partial\psi}{\partial t}. \)
Dit ziet er misschien ingewikkeld uit, maar wat belangrijk is, is de \( \hat{p} \) in de vergelijking: dit beschrijft namelijk de meting van de impuls waar ik het eerder over had. In zijn geheel staat de term die tussen de haakjes staat aan de linkerkant van de vergelijking bekend als de Dirac-operator. Omdat de Dirac-operator alleen is opgebouwd uit de meting van de impuls samen met enkele constantes (namelijk een massa en de lichtsnelheid), kunnen we concluderen dat de Dirac-operator níét commuteert met het meten van positie. Zo zien we dat in ieder geval een deel van de spectraallijnen gedefinieerd wordt op de gewenste manier, namelijk op een manier die niet commuteert met een meting van de positie.
De Schrödingervergelijking kun je zien als een speciaal geval van de Diracvergelijking, wat verklaart waarom we alleen de laatstgenoemde bekeken. Met de Schrödingervergelijking kan ook de Rydbergvergelijking worden afgeleid. Zo kunnen dus álle spectraallijnen in het spectrum van een atoom gevonden worden aan de hand van een meting die niet commuteert met de meting van positie, wat precies is waar we naar zochten. Dit verklaart waarom de spectrale definitie van de meter een goede definitie is.
Er is een kleine opmerking nodig bij het bovenstaande verhaal. In de spectraallijnen zijn bepaalde afwijkingen (“anomalieën”) zichtbaar die alsnog niet verklaard konden worden met de Diracvergelijking. Om deze anomalieën te verklaren is quantummechanica niet genoeg, maar is het nodig om ook de theorie van klassieke velden te verenigen met quantummechanica en speciale relativiteit. Dit wordt gedaan in quantumveldentheorie. Een specifiek voorbeeld van quantumveldentheorie is de quantumelektrodynamica, zo genoemd door Paul Dirac. Dit model vormt ook een onderdeel van het gehele standaardmodel. Maar, wees gerust, voor de definitie van de meter gooit quantumelektrodynamica geen roet in het eten.
Spectrale meetkunde
In de spectrale meetkunde, die een onderdeel vormt van de wiskundige tak van sport genaamd niet-commutatieve meetkunde, wordt de spectrale definitie van de meter heel serieus genomen. In dit onderzoeksgebied wordt heel precies gekeken hoe een meetkunde gereconstrueerd kan worden uit minimale gegevens, gegevens die spectraal zijn van aard.
Om dit goed te illustreren kunnen we gebruikmaken van een voorbeeld dat in 1966 beroemd werd gemaakt door de wiskundige Mark Kac. Het gaat om de vraag: kun je de vorm van een trommel horen? Deze vraag is al eerder langsgekomen op de Quantum Universe-website, namelijk in dit artikel. De frequenties die een trommel kan produceren hangen af van het membraan (het ‘vel’) van de trommel, dus de vraag kan anders worden verwoord als: kan de vorm van het membraan van de trommel worden herleid uit de frequenties waarmee het membraan trilt? In 1992 werd de vraag beantwoord, met als antwoord: nee, dat kan niet.
Dit antwoord was echter niet definitief. De vraagstelling bleek een te grote restrictie te stellen, door te luisteren naar de frequenties van de trommel als geheel. Als we toestaan om te luisteren naar de frequenties op specifieke plekken, kan de vorm van de trommel wél worden achterhaald. Dit kan je voor je zien als het luisteren naar het geluid op verschillende plekken langs de rand van de trommel.

In bovenstaand verhaal is de trommel slechts een illustratie. De wiskundige technieken zijn breder toepasbaar en vormen de basis van de spectrale meetkunde. Deze technieken zijn voor een groot deel te danken aan de grondlegger van de niet-commutatieve meetkunde, de Fransman Alain Connes. In de spectrale meetkunde speelt de Dirac-operator een centrale rol, zij het in een veralgemeniseerde vorm. Deze Dirac-operator wordt samengevoegd met twee andere ingrediënten: een zogeheten Hilbertruimte waar de Dirac-operator op kan werken, en een zogeheten algebra van gladde functies. Zodra deze drie ingrediënten nog aan een paar extra eisen voldoen, vormen ze samen een spectraaltripel.
De wiskundige details zijn hier gelukkig niet van belang, maar wat blijkt is dat, als we een bepaalde ruimte kiezen en we voor die ruimte een spectraaltripel opstellen, de gehele ruimte gereconstrueerd kan worden uit dit spectraaltripel. Dit heet ‘de spectrale karakterisering van variëteiten’. Bijvoorbeeld: om de lijn met de kortste afstand tussen twee punten in de ruimte te vinden, wordt gebruikgemaakt van de Diracvergelijking, die hierboven al is opgeschreven.
Maar niet alleen meetkunde kan worden gecodeerd in een spectraaltripel. Het is wiskundigen gelukt om het hele standaardmodel gekoppeld aan zwaartekracht, samen met al zijn anomalieën, te beschrijven met behulp van een spectraaltripel. Dit is iets wat bijvoorbeeld de snaartheorie, óók een theorie waarmee natuurkundigen proberen alle deeltjes en krachten te beschrijven, nog niet voor elkaar heeft gekregen.
Dat wil nog niet zeggen dat spectrale meetkunde, of in de bredere zin niet-commutatieve meetkunde, ‘beter’ is dan snaartheorie. Er zijn nog een hoop zaken onduidelijk en dus is er behoefte aan verder onderzoek. Er kan zelfs worden beargumenteerd dat niet-commutatieve meetkunde een onderdeel is van snaartheorie, alhoewel hierover de nodige discussie is. Hoe dan ook: het antwoord op de vraag ‘is alles spectraal?’, de titel van dit artikel, blijft vooralsnog dus onbeantwoord, maar hopelijk overtuigt het artikel je dat de vraag het waard is om gesteld te worden!