
Afbeelding 1. Een hologram.Een hologram is een tweedimensionale afbeelding die alle informatie over een driedimensionale situatie bevat. In de wis- en natuurkunde is holografie iets soortgelijks: een n-dimensionale ruimte kan meetkundig en natuurkundig equivalent zijn aan een ruimte met minder dimensies. Hologram: Georg-Johann Lay.
Holografie
Holografie heeft het wiskundige voordeel dat de rand van een ruimte een lagere dimensie heeft dan de ruimte zelf: de rand van iets n-dimensionaals heeft hoogstens dimensie n-1. In het voorbeeld van Maldacena, de beroemde AdS-CFT-correspondentie, wordt gekeken naar de anti-de-Sitter-ruimtetijd, ontdekt door onze landgenoot Wilem de Sitter (1872-1934). Deze (3+1)-dimensionale ruimtetijd heeft een 3-dimensionale rand. De “meetkundes” en zelfs de “natuurkundes” van beide ruimtes zijn equivalent: alle meetkunde (en natuurkunde) van de (3+1)-dimensionale anti-de-Sitter-ruimtetijd kun je vertalen naar zijn 3-dimensionale rand. Voor natuurkundigen is het vooral interessant dat de theorie met zwaartekracht in de anti-de-Sitterruimte equivalent blijkt te zijn met een theorie zonder zwaartekracht op de rand. En daarmee verdwijnt dan het probleem van de quantisatie van de zwaartekracht!
Wie veel meer wil lezen over al deze algemene ideeën kan dat doen in ons dossier over snaren en holografie. In dit artikel gaan we uitgebreid in op een eenvoudig voorbeeld van wiskundige holografie: de equivalentie van de meetkundes van het hyperbolische vlak en van de projectieve lijn. Het mooie is dat dit voorbeeld heel expliciet kan worden uitgewerkt en maar weinig voorkennis vereist. Het is mooi om te zien hoe goede oude wiskundige ideeën relevant blijven in de modernste natuurkunde. Op die natuurkunde zelf gaan we in dit artikel niet veel dieper in.
Bolmeetkunde
Voordat we naar het hyperbolische vlak gaan, kijken we eerst naar de meetkunde van het boloppervlak, ook wel de 2-sfeer genoemd. De dimensie is 2, omdat je 2 coördinaten nodig hebt – denk aan noorderbreedte en oosterlengte op het aardoppervlak – om een punt op dit oppervlak vast te leggen. De kortste afstand tussen twee punten vind je door de sfeer te snijden met het vlak dat door die twee punten en het middelpunt van de bol gaat – zie afbeelding 2. Die doorsnede is een cirkel. Zo’n cirkel wordt grote cirkel genoemd. Voorbeelden zijn de evenaar op aarde en de cirkel die wordt gevormd door de nulmeridiaan (door Greenwich) en door de meridiaan op 180 graden wester- en oosterlengte. De grote cirkel door Amsterdam en Los Angeles gaat langs IJsland. Daarom vlieg je dus zo noordelijk: dat is de kortste weg. Zo’n kortste pad wordt een geodeet genoemd.
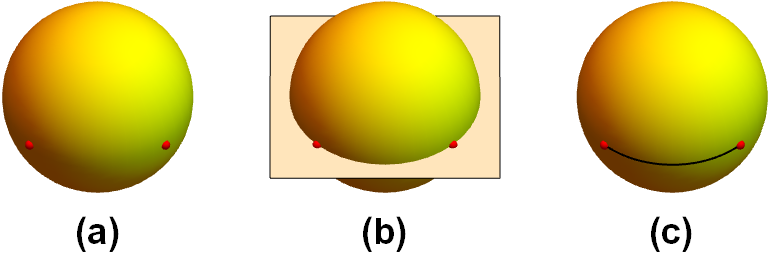
Afbeelding 2. Een geodeet.Om de kortste weg tussen twee punten op een bol (a) te vinden, teken je eerst een vlak door die twee punten en het middelpunt van de bol (b). Het vlak snijdt de bol in een grote cirkel; de kortste weg (c) volgt precies deze grote cirkel.
Als je het bolle aardoppervlak afbeeldt op een plat vlak, krijg je altijd vertekening. Afstanden die op de kaart gelijk zijn, zijn dat in werkelijkheid niet, en omgekeerd. Meestal kloppen ook de hoeken en de verhoudingen van oppervlakten niet en in het algemeen worden geodeten op de bol (grote cirkels) niet afgebeeld op geodeten in het vlak (rechte lijnen). Er zijn echter kaarten waarop de verhouding van oppervlakten wel klopt (cilindrische projectie) of waarop de hoeken kloppen (stereografische projectie).
Een driehoek in het gewone platte vlak bestaat uit 3 punten die niet op een lijn liggen en die je verbindt met lijnstukken. Analoog kun je een driehoek op de sfeer definiëren, waarbij de lijnstukken segmenten van geodeten (grote cirkels) zijn. Neem bijvoorbeeld de noordpool en twee punten op de evenaar, namelijk het punt op de nulmeridiaan en het punt op 90° oosterlengte – zie afbeelding 3. Deze punten vormen een gelijkzijdige driehoek met drie loodrechte hoeken! Zo’n driehoek bestaat niet in het platte vlak, wat bewijst dat iedere platte kaart van het bolle aardoppervlak vertekening moet vertonen. Voor iedere driehoek op een bol geldt dat de hoekensom groter is dan 180°. Het hoekoverschot, dus de hoekensom minus 180°, is rechtevenredig met de oppervlakte van de driehoek. Heel kleine driehoekjes hebben dus maar een heel klein hoekoverschot. (Een driehoek op het aardoppervlak met een oppervlakte van 1 m2 heeft een hoekoverschot van 10-12 graad.)
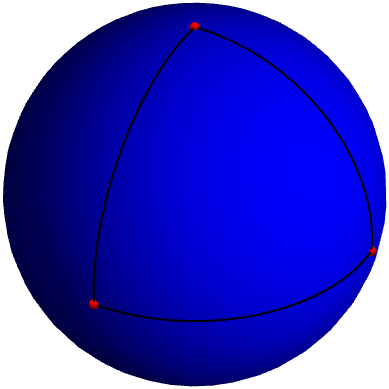
Afbeelding 3. Een driehoek op een bol.Door de noordpool (langs grote cirkels) te verbinden met twee punten op de evenaar, kunnen we op de bol een driehoek tekenen waarvan alle drie de hoeken 90 graden zijn.
Het hyperbolische vlak
Wij hebben geluk dat we ons een boloppervlak kunnen voorstellen en ook vertrouwd zijn met platte kaarten van dat oppervlak. Als je op zo’n kaart in ieder punt een formule hebt voor de lengte van korte lijnstukjes, dan heb je de bol eigenlijk niet meer nodig. De platte kaart plus deze formule bepaalen dan de meetkunde van de bol. Zo’n formule wordt metriek genoemd. Bernhard Riemann (1826-1866) bedacht dat we dus allerlei nieuwe meetkundes kunnen uitvinden door verschillende metrieken te bedenken! Dat idee is fundamenteel in Einsteins algemene relativiteitstheorie.

Afbeelding 4. Een platte projectie van het hyperbolische vlak.Het hyperbolische vlak is gevuld met even grote driehoeken, die vervolgens zo vervormd zijn dat ze in het tweedimensionale vlak passen. Afbeelding: Anton Sherwood.
In afbeelding 4 zie je een voorbeeld van zo’n Riemannse meetkunde. Deze meetkunde heet het hyperbolische vlak. Net zoals bij platte afbeeldingen van de bol is er sprake van vertekeningen. De driehoeken lijken naar de rand steeds kleiner te worden, maar in werkelijkheid zijn ze allemaal even groot! De geodeten (`rechte lijnen’) in deze meetkunde zijn de halve lijnen en halve cirkels die loodrecht op de rand staan. Deze geodeten zijn oneindig lang, want hoe dicht je ook bij de rand zit, tot de rand heb je altijd nog oneindig veel driehoeken te gaan en alle driehoeken zijn even lang, ondanks de vertekening.
Er zijn twee typen hyperbolische lijnen: halve cirkels en halve lijnen loodrecht op de rand. We hebben ze echt allebei nodig, want we willen – net als in het platte vlak – dat door ieder tweetal punten een hyperbolische lijn gaat.
Nu wat goed nieuws: in tegenstelling tot lengtes, oppervlaktes en geodeten zijn de hoeken in afbeelding 4 niet vertekend. De hoeken die we met onze euclidisch getrainde ogen zien, zijn ook de hoeken van de hyperbolische meetkunde. Als je nu naar een driehoek kijkt op het hyperbolische vlak, dan zie je dat de hoekensom kleiner is dan 180°. Het hoektekort, dus 180° minus de hoekensom, blijkt rechtevenredig te zijn met de oppervlakte van de driehoek. Net als op de bol is voor kleine driehoekjes de hoekensom dus wel bijna gelijk aan 180°.
Isometrieën
In de wiskunde is het bij iedere structuur belangrijk te onderzoeken welke afbeeldingen die structuur behouden. In de euclidische meetkunde bekijken we dus afbeeldingen van het vlak naar zichzelf die de afstand bewaren. Deze afbeeldingen worden isometrieën genoemd. Een voorbeeld van zo’n isometrie in het platte vlak is de loodrechte spiegeling in een lijn, kortweg lijnspiegeling genoemd. Zo’n lijnspiegeling behoudt afstand, want als je een lijnstuk spiegelt, krijg je een lijnstuk van dezelfde lengte. Door verschillende lijnspiegelingen te combineren, krijg je andere isometrieën zoals rotaties, translaties en puntspiegelingen.
In het hyperbolische vlak geldt vrijwel hetzelfde. Ook daar kun je loodrechte lijnspiegelingen definiëren, waarbij de `lijn’ een hyperbolische lijn is, een geodeet, dus zo’n halve lijn of halve cirkel loodrecht op de rand. Dit is een hyperbolische isometrie: een afbeelding van het hyperbolische vlak naar zichzelf die de hyperbolische afstand bewaart. Door deze hyperbolische lijnspiegelingen te combineren krijg je alle andere hyperbolische isometrieën. Er bestaan hyperbolische versies van rotaties en van puntspiegelingen.
Als je een lijnspiegeling toepast op een figuur, krijg je het spiegelbeeld. Dat spiegelbeeld ziet er in het algemeen anders uit. Wiskundigen zeggen dat de figuren omgekeerd georiënteerd zijn. Als je twee lijnspiegelingen toepast, dan krijg je weer de oorspronkelijke oriëntatie. Dat is het geval bij rotaties, translaties en puntspiegelingen. Deze worden daarom oriëntatiebehoudend genoemd, terwijl lijnspiegelingen oriëntatie-omkerend zijn. Precies hetzelfde geldt in het hyperbolische vlak.

Afbeelding 5. Spiegelingen en oriëntatie.Een spiegeling draait oriëntatie om. Vanaf de bergtop gezien staan de donkere bomen links en de lichte bomen rechts. Vanaf de gespiegelde bergtop bekeken staan de donkere bomen juist rechts en de lichte links. Foto: Oregon’s Mt. Hood Territory.
Al het bovenstaande kan ook in formules precies gemaakt hebben. In de web-versie van dit artikel laten we het rekenwerk weg, maar wil je zelf eens wat met de formules spelen (daarvoor heb je aan middelbare-schoolwiskunde genoeg), dan kun je de langere versie van dit artikel downloaden waarin alle formules te vinden zijn.
Van het vlak naar de rand
Als je afbeelding 4 nog eens bekijkt zie je direct wat de rand van het hyperbolische vlak is: dat is een cirkel. Nu moet je daarbij bedenken dat die cirkel eigenlijk oneindig groot is – in de afbeelding zijn alle driehoekjes aan de buitenkant immers oneindig verkleind. Je kunt de cirkel dus ook zien als een oneindig lange reële getallenlijn, met een punt “toegevoegd op oneindig” om de twee uiteinden van die getallenlijn aan elkaar te plakken tot een cirkel. Deze constructie wordt ook wel de reële projectieve lijn genoemd.
Nu terug naar de holografie: we kunnen laten zien dat de meetkunde van het tweedimensionale hyperbolische vlak precies correspondeert met de meetkunde van de eendimensionale reële projectieve lijn! Op het eerste gezicht lijkt dit een waanzinnige opmerking, maar toch blijkt deze bewering wiskundig juist. Zo kunnen we bijvoorbeeld laten zien dat:
- Geodeten in het hyperbolische vlak corresponderen met paren van punten in de projectieve lijn: elke geodeet kun je, zoals we hierboven al zagen, uniek definiëren aan de hand van zijn eindpunten.
- De isometrieën van het hyperbolische vlak die we hierboven beschreven precies corresponderen met bepaalde afbeeldingen – projectieve transformaties – van de reële projectieve lijn naar zichzelf. Een spiegeling in de hyperbolische lijn correspondeert zo met een soort van spiegeling in de twee eindpunten ervan.
- Punten in het hyperbolische vlak corresponderen met bepaalde projectieve transformaties van de projectieve lijn. Waarom met projectieve transformaties? Omdat je een punt in het vlak kunt definiëren als het vaste punt onder een puntspiegeling – een punt definieert dus een isometrie van het vlak. Omdat isometrieën (zie het punt hierboven) corresponderen met projecieve transformaties van de rand, kun je dus ook een correspondentie van elk punt met een projectieve transformatie van de rand vinden.
Zo kun je verder gaan: bij elke meetkundig concept in het hyperbolische vlak (het snijden van twee lijnen, het liggen van een punt op een lijn, het meten van een hoek, het meten van een afstand) kun je voor de eendimensionale reële projectieve lijn een corresponderend concept vinden. Zoals gezegd: ben je geïnteresseerd in de precieze wiskunde daarachter, lees dan vooral de lange versie van dit artikel.
Natuurkunde

Afbeelding 6. Évariste Galois (1811-1832).Artiest onbekend.
Wat doet al deze wiskunde op een natuurkundewebsite? Het punt is dat veel wiskunde (zelfs theoretische, schijnbaar wereldvreemde wiskunde die door wiskundigen is ontwikkeld uit puur mathematische motieven) de opmerkelijke gewoonte heeft vroeg of laat in de natuurkunde op te duiken. Holografie is een voorbeeld hiervan. Hierboven zagen we een eenvoudig, precies en clean voorbeeld van holografie binnen de meetkunde. Dat voorbeeld kan helpen het principe achter complexere versies van holografie zoals de AdS/CFT-correspondentie uit de moderne natuurkunde te begrijpen.
Op de avond voor zijn fatale duel schreef de 20-jarige Évariste Galois (1811-1832) hoe je kunt bewijzen dat er geen wortelformule bestaat voor vergelijkingen van graad 5. Hij deed dat met symmetrieën. Uit dit werk ontstond groepentheorie, de abstracte wiskundige studie van symmetrieën. Veertig jaar later stelde Felix Klein in zijn Erlanger Programma (1862) voor om groepen en symmetrieën centrum en startpunt van de meetkunde te maken. Tussendoor vond Bernhard Riemann de abstracte gekromde meetkunde uit.
Wat heeft deze 19e-eeuwse wiskunde nu met 21ste-eeuwse natuurkunde te maken? In Einsteins speciale relativiteitstheorie (Minkowski-meetkunde) spelen Lorentztransformaties een centrale rol en in zijn algemene relativiteitstheorie doen de coördinaattransformaties dat. In de quantummechanica waren groepentheoretische ideeën zo succesvol dat Wigner gefrustreerd sprak van Gruppenpest. In de deeltjesfysica spelen symmetrieën een fundamentele rol in de beschrijving van deeltjes en hun interactie. En in de beroemde AdS/CFT-correspondentie van Juan Maldacena zien we weer het oude holografische idee van Felix Klein: twee structuren (meetkundes) met dezelfde symmetrieën zijn equivalent. Wigner zou vast weer spreken van de unreasonable effectiveness of mathematics in the natural sciences.
Afbeelding blokkenschema: het driedimensionale equivalent van het hyperbolische vlak. Afbeelding: Claudio Rocchini.