Hoe kunnen we zeker weten dat de aarde rond is? Voor velen is deze foto, gemaakt vanuit het International Space Station, een overtuigend argument:

Afbeelding 1. Voor astronauten is het duidelijk: de aarde is rond.Foto: NASA/Samantha Cristoforetti
Maar wat als de NASA ons allemaal voor het lapje heeft gehouden? Wat als de astronauten allemaal liegen, en de beroemde maanlanding inderdaad in een studio in Hollywood gefilmd is? Het is nog niet zo makkelijk om op eigen houtje een raket te maken die hoog genoeg kan komen om de kromming van de aarde te zien. Is er een laag-bij-de-grondse manier om erachter te komen of de aarde daadwerkelijk rond is?
Je zou bijvoorbeeld in de haven kunnen gaan zitten en uitvarende schepen gaan bekijken. Als de lucht helder genoeg is, kun je een schip achter de horizon als het ware in de zee zien zinken. Maar dat zou ook kunnen betekenen dat de aarde de vorm van een cilinder heeft, en dat het schip toevallig langs de cirkelrichting van de cilinder vaart. Zo kun je tegen veel van de argumenten dat de aarde bolvormig is wel ietsinbrengen. Er is zelfs een online vereniging opgericht die zich daarmee bezighoudt.
Wat als er geen schepen in de buurt zijn, en je geen ruimteraket tot je beschikking hebt? Stel dat je op een groot, weids open weiland staat – hoe zou je dan de kromming van de aarde kunnen meten? Een mogelijk antwoord komt voort uit de landmeetkunde.

Afbeelding 2. Landmeters in Idaho, 1910.Foto:
De beroemde Duitse wiskundige Carl Friedrich Gauss kreeg in het begin van de negentiende eeuw de opdracht om landmetingen te verrichten in het toenmalige koninkrijk van Hannover. Hij trok vele zomers te paard door het Duitse land, en kreeg naar aanleiding daarvan een revolutionair idee over kromming. Hoewel hij op dat moment al veel spectaculaire ontdekkingen in de wiskunde op zijn naam had staan, was Gauss zo trots op dit idee dat hij het in zijn notities zijn ‘fantastische stelling’ noemde.
Afbeelding 3. Carl Friedrich Gauss.Lithograaf uit ‘Astronomische Nachrichten’.
Om het idee van Gauss te begrijpen, is het handig om na te denken over een mier die over een vel papier loopt. Zijn wereld lijkt tweedimensionaal. Als het vel plat op tafel ligt, kan de mier in elke richting lopen zonder kromming te merken. Maar als we het vel oprollen tot een cilinder, is er één richting die gekromd is. Als de mier langs deze richting loopt, zal hij merken dat zijn wereld in die richting naar voren helt. Hij leeft echter nog steeds op hetzelfde vel papier, en wij als driedimensionale wezens kunnen zien dat het platte vlak en de cilinder in die zin hetzelfde zijn.
Dit wordt anders zodra we de mier op een bol zetten. In tegenstelling tot een cilinder kun je géén bol maken van een enkel plat vel papier. Als driedimensionale wezens kunnen wij dat na een tijdje knutselen met papier en plakband makkelijk zien. Het grote inzicht van Gauss is echter dat óók de mier dit onderscheid tussen een bol en een cilinder in zijn tweedimensionale wereld kan maken!
Als de mier op een cilinder loopt, kan hij in één richting positieve kromming merken. In de andere richting, langs de lange zijde van de cilinder, is de kromming nul. Het product van de krommingen in beide richtingen, nul keer iets wat niet nul is, is dus ook nul, net als voor een vel papier. Voor een bol is er echter positieve kromming in beide richtingen, en het product van de twee krommingen is dus ook positief. Met deze grootheid, die ook wel de Gauss-kromming genoemd wordt, kunnen we een bol van een vlak of cilinder onderscheiden! Om die reden wordt de Gauss-kromming ook wel intrinsiek aan een oppervlakte genoemd.
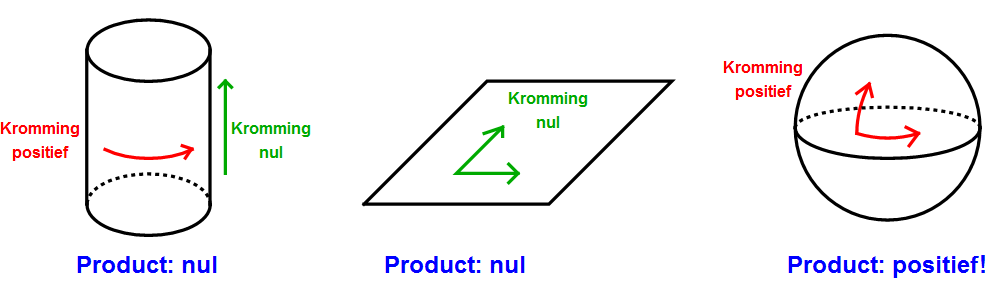
Afbeelding 4. Kromming en Gauss-kromming.Een cilinder en een plat vla hebben allebei Gauss-kromming nul; een bol niet.
Omdat de aarde zo groot is, is het niet makkelijk om de kromming in één bepaalde richting direct te meten. Het mooie van de Gauss-kromming is echter dat deze gevolgen heeft voor alle meetkunde op een oppervlak. Op een oppervlak waarop de Gauss-kromming nul is, zoals een plat vlak of een cilinder, tellen de hoeken van een driehoek bijvoorbeeld altijd op tot 180 graden. Als de Gauss-kromming positief is, wordt de som van de drie hoeken meer dan 180 graden. Door de hoeken te meten van een grote driehoek in het landschap, bijvoorbeeld tussen drie kerktorens, kun je dus aantonen dat de aarde geen plat vlak én geen cilinder kan zijn! Daarbij moeten de kerktorens natuurlijk wel behoorlijk ver van elkaar af staan, en je zult de hoeken met heel grote nauwkeurigheid moeten meten.
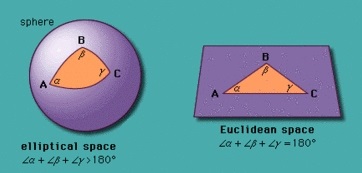
Afbeelding 5. Een driehoek op een vlak en een bol.
Afbeelding: British International School, Phuket.
Deze ideeën van Gauss werden later door zijn even zo bekende student Bernhard Riemann verder uitgewerkt. Riemann ontdekte ook in hogere dimensies zulke intrinsieke krommingen als de Gauss-kromming. Zijn constructies zouden later een hoofdrol spelen in Einsteins algemene relativiteitstheorie. In die theorie kan de ruimtetijd een soortgelijke intrinsieke kromming hebben – iets wat bijvoorbeeld ontdekt werd door onze landgenoot Willem de Sitter.