Afbeelding 1. Een telraam.Met een telraam kun je goed gehele getallen optellen. Maar wat doe je als je oneindig veel gehele getallen wilt optellen?
De vraag uit de inleiding lijkt maar één mogelijk antwoord te hebben:
1 + 2 + 3 + 4 + 5 + … = oneindig
De optelsom wordt immers steeds groter, en stijgt uiteindelijk uit boven elke eindige grens. Toch is er een zeer verrassend tweede antwoord op deze vraag, namelijk:
1 + 2 + 3 + 4 + 5 + … = -1/12
Min een twaalfde??? Hoe kan dat ooit het juiste antwoord zijn? Een leuke redenering die tot dit antwoord leidt, zien we in het onderstaande filmpje van het YouTube-wiskundekanaal Numberphile:
Maar waarom zou dit laatste antwoord juist zijn, en in dat geval: in welke betekenis is het dan “juist”? En hebben we er ooit in de natuurkunde iets aan?
Een oneindige som?
Laten we allereerst opmerken dat we in de natuur zelden daadwerkelijk oneindig veel getallen optellen. Als mijn collega-natuurkundige I. op 1 januari één biertje drinkt, op 2 januari twee biertjes, op 3 januari drie, enzovoort, dan is “hoeveel biertjes heeft I. uiteindelijk op?” geen erg goed geformuleerde vraag. In de praktijk zullen we op een bepaald moment meten hoeveel biertjes I. daadwerkelijk achter de kiezen heeft, en dat zal een heel groot, maar eindig getal zijn.
Extrapoleren we het bovenstaande proces naar het oneindige, dan zou I. in theorie oneindig veel biertjes opdrinken. In die zin is het eerste antwoord, “oneindig”, dus het juiste antwoord. Hetzelfde geldt als we eerst 1 baksteen op een vrachtwagen laden, dan 2, dan 3, enzovoort. Hoeveel bakstenen liggen er dan uiteindelijk op de vrachtwagen? We kunnen niet daadwerkelijk alle termen optellen, maar de eindige deelsommen worden steeds groter, en dus is “oneindig” het best mogelijke antwoord.
Een écht oneindige som
Toch komen in de natuurkunde soms problemen voor waarbij we daadwerkelijk in één keer oneindig veel termen optellen. Een dergelijk probleem komt bijvoorbeeld voor in de snaartheorie. Die theorie, waarover we all eens een uitgebreid dossier schreven, gaat ervan uit dat de bouwstenen van ons heelal kleine trillende snaartjes zijn, in plaats van puntvormige deeltjes.
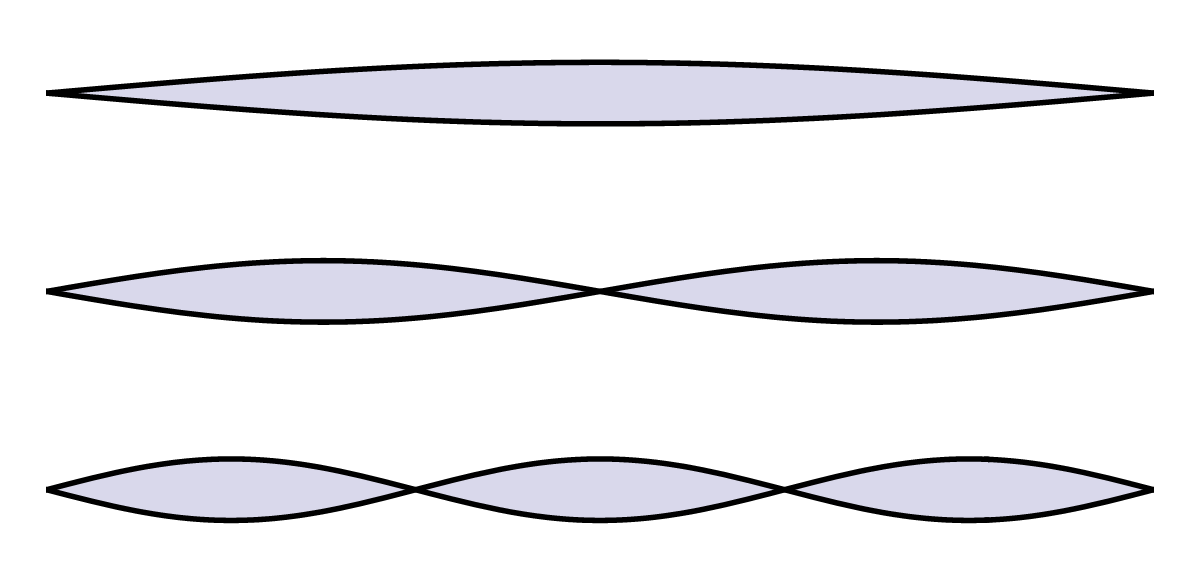
Afbeelding 2. Trillingen in een snaar.De trilling kan precies éénmaal op de snaar passen, precies tweemaal, precies driemaal, enzovoort.
Nu kan een snaar op verschillende manieren tellen: de trilling kan precies één keer op de snaar passen, of twee keer, of drie keer, enzovoort – zie de afbeelding hierboven. Een snaar hoeft echter niet precies in één van deze ’tonen’ te trillen: een daadwerkelijke trilling van de snaar kan ook bestaan uit een trilling van de eerste soort in combinatie met één van de tweede soort, één van de derde soort, enzovoort. In een realtistische trilling komen dus oneindig veel verschillende ‘basistrillingen’ voor!
Dit laatste heeft tot gevolg dat we in allerlei berekeningen in de snaartheorie rekening moeten houden met álle mogelijke trillingen die door een snaar kunnen lopen. We moeten dan uiteindelijk alle antwoorden voor die individuele trillingen optellen, en dat kan leiden tot uitdrukkingen van de vorm 1+2+3+…, waarbij we nu echt alle termen moeten meenemen.
Uit zo’n écht oneindige optelsom kan natuurlijk nooit oneindig komen, want wat we ook aan een snaar meten – zijn massa, zijn energie, noem maar op – het antwoord zal altijd een eindig, meetbaar getal zijn. Natuurkundigen moeten dus op zoek naar een truc om uit zo’n schijnbaar oneindige optelsom een fysisch, eindig antwoord te destilleren – en de in het filmpje uitgelegde truc blijkt daarvoor precies de juiste te zijn!
Nu moet je met trucs altijd voorzichtig zijn. Laten we dus direct vermelden dat er nog allerlei andere, meer rigoreuze methodes zijn om de optelsom van de vorm ‘1+2+3+…’ in de snaartheorie uit te rekenen of zelfs geheel te vermijden. Uit al die andere berekeningen vinden we uiteindelijk hetzelfde antwoord, dus bent u door onze collega’s van Numberphile niet overtuigd, maakt u zich dan niet te veel zorgen. De methode laat voor strikte wiskundigen zeker te wensen over, maar leuk is die wel – en het antwoord klopt ook nog eens!
De optelling 1+2+3+… komt in de snaartheorie dus als tussenstap in allerlei berekeningen voor. Eén voorbeeld van een resultaat wat op deze manier afgeleid kan worden, is het feit dat snaartheorie alleen écht werkt als de ruimte waarin de snaar trilt tiendimensionaal is. Maar hoe je dat precies uitrekent is weer een heel verhaal op zichzelf… iets voor een volgend artikel!
Afbeelding blokkenschema: Anssi Koskinen. Met dank aan Ivo van Vulpen voor de inspiratie voor dit artikel.