Maar goed, veronderstel bij wijze van gedachte-experiment dat je de fysica gekraakt hebt: dat er een theorie bestaat die alle fundamentele deeltjes en de natuurwetten waaraan deze onderhevig zijn tot op ongekende precisie beschrijft. Betekent dit dan het einde van de wetenschap? Feitelijk valt er niets nieuws meer te ontdekken, omdat elk verschijnsel op een of andere manier terug te leiden zou moeten zijn tot een van de reeds bekende natuurwetten.

Afbeelding 1. Een theorie van alles.Bestaat er een onderliggende, fundamentele theorie van alles waaruit elke andere wetenschap afgeleid kan worden? Comic getekend door Randall Munroe voor XKCD.
De opvatting dat elk denkbaar verschijnsel te reduceren is tot een lijst van basisprincipes wordt in de filosofie reductionisme genoemd. Deze opvatting ligt ten grondslag aan de moderne natuurwetenschappen. De manier waarop natuurwetenschappers proberen de wereld te begrijpen is immers door een bepaald verschijnsel te zien als een speciaal geval van iets anders: iets fundamentelers. Denk bijvoorbeeld aan het bewegen van de aarde om de zon, of het vallen van een steen naar de aarde: dat zijn speciale gevallen van de gravitatiewetten van Newton.
Op soortgelijke manier zou je een aanzienlijk deel van de natuurwetenschappen kunnen ordenen op volgorde van meest naar minst fundamenteel:
- Hoge-energiefysica (standaardmodel)
- Lage-energiefysica (meerdeeltjesfysica)
- Scheikunde
- Moleculaire biologie
- Celbiologie
- … etc.
Reductionisme betekent dat de wetmatigheden die horen bij een wetenschap in de bovenstaande lijst, begrepen kunnen worden in termen van wetmatigheden die voorkomen in de wetenschap die een plaatsje hoger op de lijst staat.
Terug naar de vraag of een theorie van alles het einde van de wetenschap zou betekenen. Al in 1972 schreef Nobelprijswinnaar en zeer gerespecteerd fysicus Philip W. Anderson een bekend artikel hierover: “More is different”. In dit artikel beweert hij dat reductionisme op zich weinig praktisch nut heeft als je niet ook in staat bent om uit de fundamentele natuurwetten alle bestaande wetenschappen op te bouwen. Dat wil zeggen: gebruikmakend van alleen de wetmatigheden van de wetenschap die op plaats 1 staat, de wetmatigheden van wetenschap op plaats 2 deduceren, waaruit je dan de wetmatigheden van de wetenschap op plaats 3 kunt afleiden, enzovoorts.

Afbeelding 2. Philip W. Anderson.Philip Warren Anderson (1923) won in 1977 de Nobelprijs voor de natuurkunde.
Nu blijkt in praktijk dat dit laatstgenoemde nagenoeg onmogelijk is. Laten we dit illustreren met de volgende metafoor.
Voetbalstadion
Stel je voor: je bent in een voetbalstadion dat tot de nok vol zit met supporters. In deze metafoor zijn de individuele supporters de fundamentele deeltjes van het systeem. De “fundamentele deeltjes” hebben de volgende bewegingsvrijheid: zij kunnen staan en zitten, of alles wat daartussenin zit. Het doel voor de hoge-energiefysicus is om de natuurwetten te vinden die het gedrag van de fundamentele deeltjes volledig beschrijven.
De wedstrijd is in volle gang. Plots wordt er gescoord. Iedereen in jouw vak gaat staan. Jij ook, anders zie je niets meer. Na een tijdje juichen gaan je directe buren weer zitten, en omdat je niet als enige wil blijven staan volg jij hun voorbeeld. Zetten we de hoge-energiefysicabril op, dan zien we dat de deeltjes een interactie met elkaar hebben, en wel als volgt: naburige deeltjes willen graag op dezelfde hoogte zijn als hun directe buren. Dan voelt iedereen zich het gemakkelijkst. Hiermee is de klus van de hoge-energiefysicus geklaard. We weten precies welke legoblokjes we tot onze beschikking hebben om ons systeem op te bouwen (de supporters, ofwel de fundamentele deeltjes), en we weten hoe deze legoblokjes op elkaar passen (de interacties tussen de fundamentele deeltjes). Gezien vanuit het perspectief van de reductionist zou nu alles wat er te weten is over ons bedachte systeem terug te voeren moeten zijn op deze hoge-energiefysicabeschrijving van het systeem.
Betekent dit echter ook dat we elke vraag die we zouden willen stellen over het systeem kunnen beantwoorden? Denk bijvoorbeeld aan vragen als: “wat gebeurt er als ik het systeem opwarm?” Of: “wat is de grondtoestand van het systeem?” Deze laatste vraag is typisch een vraag voor een lage-energiefysicus, die zich, in tegenstelling tot de hoge-energiefysicus, niet bezighoudt met wat de fundamentele deeltjes zijn, maar met wat er gebeurt als je heel veel van dit soort deeltjes samenneemt tot een groter geheel. De grondtoestand is de toestand van minimale energie. In termen van ons systeem, waarbij we nu afspreken dat “energie” gelijkstaat aan het ongemak dat twee naburige supporters ondervinden als ze zich niet op dezelfde hoogte bevinden, kunnen we concluderen dat de grondtoestand een toestand is waarbij alle supporters precies op dezelfde hoogte zitten. Dan voelt niemand zich immers ongemakkelijk en kan iedereen het spel even goed zien. Merk op dat er in dit model meerdere grondtoestanden zijn, bijvoorbeeld “iedereen staat”, of “iedereen zit”.
Wat zou er nu gebeuren als we een beetje meer energie toelaten in het systeem? Dit betekent dat naburige supporters niet meer precies op gelijke hoogte moeten zijn, maar dat er een klein hoogteverschil is toegestaan. Wat er nu volgt is voor mening voetbalfan geen verassing: we hebben hier te maken met een wave.
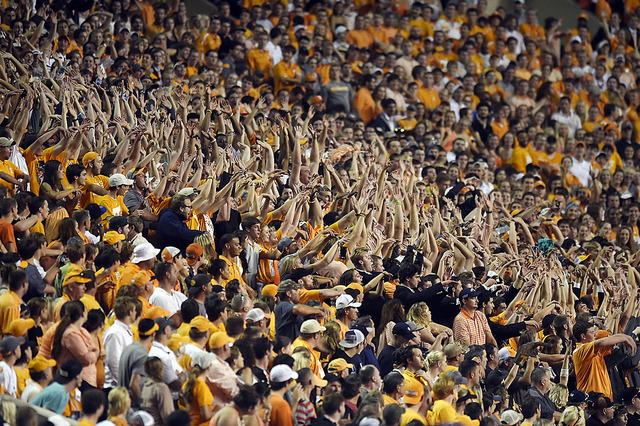
Afbeelding 3. Een wave in een voetbalstadion.Een wave zoals deze is een grootschalig effect, dat op het niveau van de individuele supporters erg lastig te beschrijven is. (Bron.)
Daar waar de hoge-energiefysicus zich midden in het stadion bevindt, en alle details goed in de gaten houdt, zien we de lage-energiefysicus zitten bovenin de skybox waar zij een goed overzicht heeft over het gehele stadion. Gezien vanuit haar ogen, is het veel efficiënter om het systeem te beschrijven in termen van de ontstane golven, die elk beschreven kunnen worden met slechts een paar parameters (snelheid, positie op een gegeven vast tijdstip, etc.), in tegenstelling tot de gigantische hoeveelheid data die nodig is om alle posities van alle supporters die deel uitmaken van de wave in de loop van de tijd bij te houden.
Quasideeltjes
Bekeken door de ogen van de lage-energiefysicus, die de onderlinge supporters niet zo goed kan zien, zou je zelfs geneigd zijn te concluderen dat de golven op zich de fundamentele deeltjes van het systeem zijn! In vakjargon worden deze golven ook wel quasideeltjes genoemd, omdat zij weliswaar geen echte deeltjes zijn, maar eigenschappen hebben die ook aan werkelijke deeltjes toegekend kunnen worden: snelheid, positie, etc.
We zien dat we in het bovenstaande voorbeeld twee manieren hebben om hetzelfde systeem te beschrijven: in termen van supporters (fundamentele deeltjes), of in termen van golven (quasideeltjes). Dit zijn twee totaal verschillende manieren van kijken naar hetzelfde systeem. Het beeld van de fundamentele deeltjes is nauwkeuriger, maar het beeld van de golven is praktischer, met name als het gaat om het beantwoorden van vragen over het algehele gedrag van het totale systeem, wat in termen van de fundamentele deeltjes veel en veel meer rekenwerk vereist dan wanneer wij ons richten op de beschrijving in termen van quasideeltjes.
Het punt is nu dat het voor de hoge-energiefysicus, die zich te midden van alle supporters bevindt, lastig is om de golven in hun geheel te zien. Hij ziet alleen individuele supporters af en toe opstaan, en dan weer zitten. Om de golven waar te nemen is het nodig om het stadion van veraf te bekijken. De golfbeschrijving kan niet direct – dat wil zeggen zonder het systeem in zijn geheel nader te bestuderen – worden afgeleid uit de theorie van de fundamentele deeltjes.
Emergente theorieën
Toegepast op werkelijke fysische systemen, waarbij we te maken hebben met een heleboel (vaak wel 1023) deeltjes per systeem, wordt de lage-energiefysicus gedwongen tot het bedenken van een alternatief beeld zoals dat van de golven in het voetbalstadion. Denk bijvoorbeeld aan de manier waarop vloeistofstromen gemodelleerd worden: het is onzinnig om de bewegingen van elk individueel molecuul bij te houden. In plaats daarvan beschrijven we de vloeistof als een continuüm dat voldoet aan bepaalde bewegingswetten, beter bekend als de Navier-Stokesvergelijkingen. Dit alternatieve beeld van het systeem wordt een emergente theorie genoemd, omdat deze ontstaat uit het collectieve gedrag van grote hoeveelheden fundamentele deeltjes. In zo’n theorie wordt alles uitgedrukt in termen van de quasideeltjes en de interacties die zij met elkaar aangaan; de fundamentele deeltjes komen in deze beschrijving niet meer voor.

Afbeelding 4. Een watergolf.Een bak water bevat al snel 1023 watermoleculen. Hier is het gebruik van emergente beschrijvingen dus nog veel belangrijker dan in het voorbeeld van het voetbalstadion. (Bron.)
Terug naar de hoofdvraag. Stel nu dat we een theorie van alles in handen hebben. Weten we dan alles wat er te weten valt? Philip W. Anderson beweerde van niet, omdat voor het beantwoorden van praktische vragen in bijna alle gevallen een bijbehorende emergente theorie nodig is. Het bedenken van de juiste emergente theorie is echter een vak apart, precies omdat deze emergente theorie op het eerste gezicht heel verschillend kan zijn van de onderliggende fundamentele theorie. We mogen hieruit concluderen dat elke natuurwetenschap op zijn eigen manier fundamenteel is. En als we ooit al zo gelukkig zijn om een theorie van alles ontdekken, dan is dat niet het einde van de wetenschap, maar pas het begin.