Basisbegrippen
Om te kunnen begrijpen hoe zulke metershoge golven ontstaan, moeten we natuurlijk eerst snappen hoe zeegolven überhaupt werken. Net als licht kan ook het profiel van een zeegolf in voldoende diep water schematisch worden beschouwd als sinusoïde zoals te zien in afbeelding 1. Hierin zijn de golflengte L, de horizontale afstand tussen twee opeenvolgende toppen (ook wel kammen genoemd), en de hoogte H, het hoogteverschil tussen de hoogste en laagste punten van het golfprofiel, aangegeven. Andere belangrijke begrippen zijn de periode T, de tijd die op een bepaald vast punt verloopt tussen het passeren van twee opeenvolgende golfkammen, en de voortplantingssnelheid C, de snelheid waarmee de golf zich verplaatst.
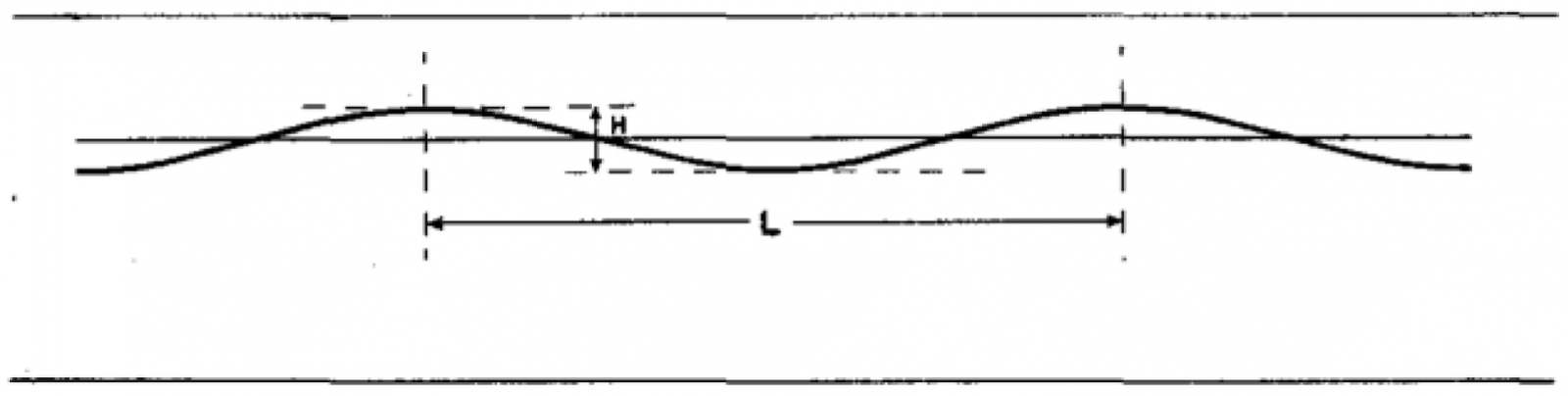
Afbeelding 1. Het profiel van een zeegolf.L is in deze schets de golflengte en H de golfhoogte. Afbeelding uit Zeegolven, P. Groen en R. Dorrestein , KNMI 1976.
De voortplantingssnelheid
Het zal je misschien niet verbazen dat de voortplantingssnelheid kan worden berekend met het verband C = L / T. In een tijd T schuift de golf immers één golflengte, dus L meter op, dus de snelheid is de afgelegde afstand gedeeld door de tijd: L / T. Waarnemingen wijzen verder uit dat de voortplantingssnelheid ook kan worden berekend met een formule die van de golflengte L en de diepte D afhangt. Deze formule is een stuk ingewikkelder en ziet er in zijn volle glorie als volgt uit:
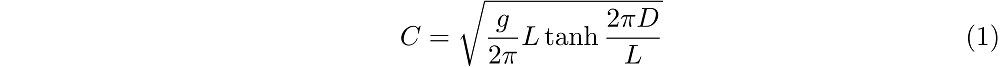
Hierin stelt g de zwaartekrachtsversnelling voor die een waarde van ongeveer 9,81 m/s2 heeft. Misschien schrik je van de vorm van deze formule, maar als we de tanh, de ’tangens hyperbolicus’, beter bekijken, kunnen we zien dat de uitdrukking voor erg diepe en erg ondiepe wateren een stuk vereenvoudigt.
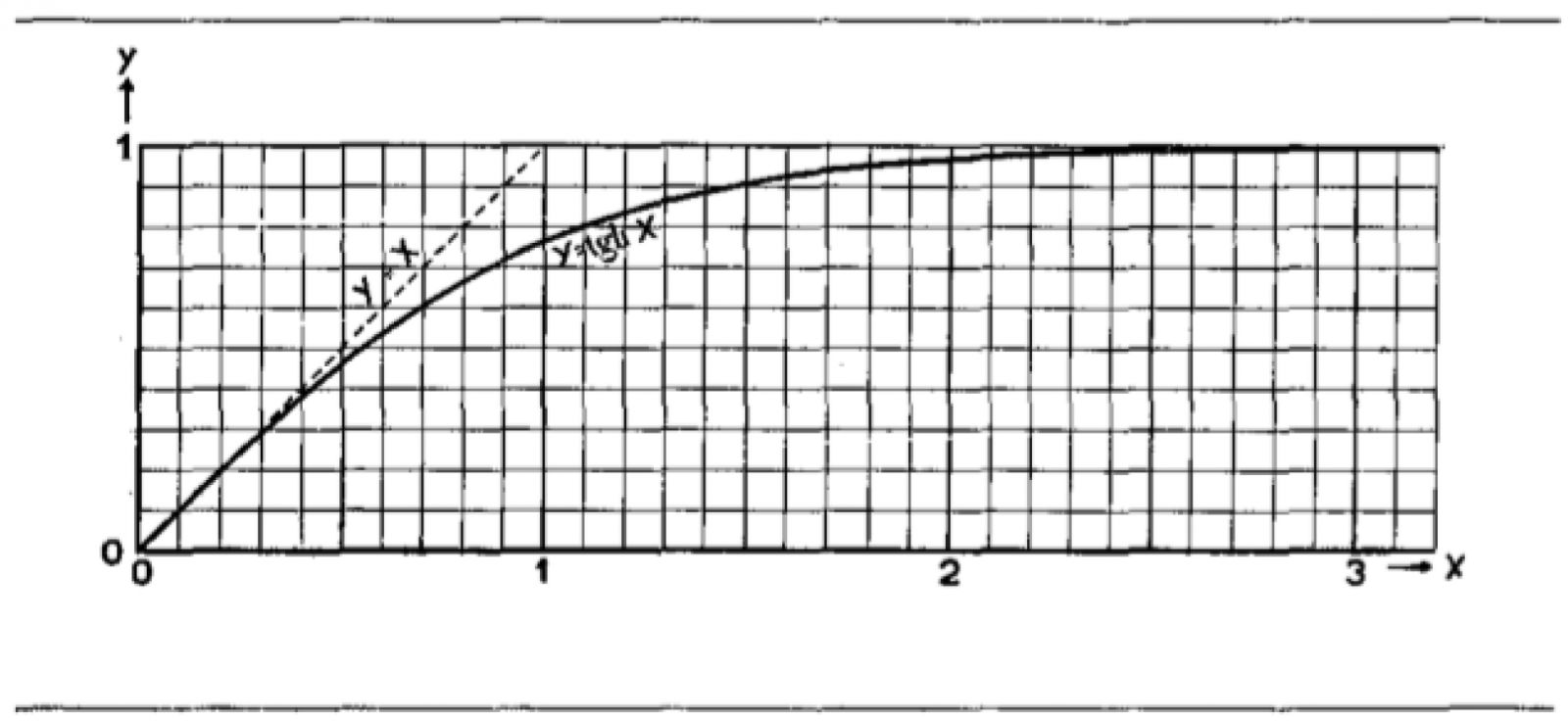
Afbeelding 2. Grafische voorstelling van de tangens hyperbolicus.Voor lage waarden van x nadert tanh x het lineaire verband y = x, zoals aangegeven door de stippellijn. Voor grote waarden van x nadert tanh x de waarde 1. Afbeelding uit Zeegolven, P. Groen en R. Dorrestein , KNMI 1976.
De tangens hyperbolicus van x wordt gegeven door de formule
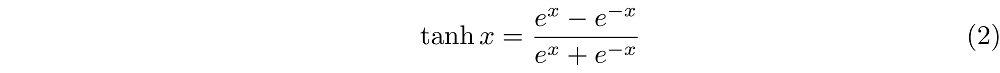
In afbeelding 2 wordt deze functie grafisch weergegeven. Om de formule voor C te gebruiken, moeten we in de grafiek van afbeelding 2 de waarde van 2πD/L als horizontale coördinaat opzoeken en kunnen dan de waarde van tanh(2πD/L) als verticale coördinaat aflezen. We kunnen in de grafiek twee gevallen onderscheiden: als 2πD/L heel groot is, en als die waarde juist heel klein is. In het eerste geval zien we dat de waarde voor tanh(2πD/L) de waarde 1 nadert. Voor grote waarden van D, op plekken waar golven zich boven een relatief diepe zeebodem bevinden, reduceert de ingewikkelde formule voor C dus tot
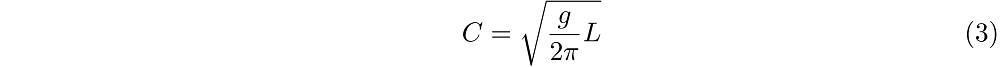
Opmerkelijk aan dit verband is dat in diepe wateren de snelheid van de golf helemaal niet van de precieze diepte afhangt! In het tweede geval, als 2πD/L klein is, kan de grafiek van tanh(2πD/L) benaderd worden als een lineair verband, zoals de stippellijn in afbeelding 2 laat zien. Dat wil zeggen: tanh(2πD/L) ≈ 2πD/L Als we dit invullen in de formule voor C, zien we dat in ondiep water de voortplantingssnelheid van de golven wordt gegeven door
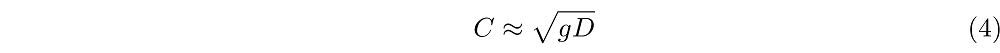
We zien dus dat de voortplantingssnelheid van een golf in ondiep water helemaal niet meer zo ingewikkeld is en bovendien dat een golf in ondiep water zich steeds trager voortbeweegt naarmate het water minder diep wordt.
De energie
Golven hebben natuurlijk niet alleen een voortplantingssnelheid, ze hebben ook een energie. Zoals je misschien herkent uit problemen waar een karretje van een heuvel afrijdt, bestaat ook bij golven de energie uit de som van de potentiële en de kinetische energie. De potentiële energie zit bij golven opgeslagen in de vervorming van het wateroppervlak. Het is de energie die nodig is om het water in de kammen op te tillen. De kinetische energie zit in de beweging van de waterdeeltjes. Er is berekend dat zolang de golfhoogte veel kleiner is dan de diepte de som van de potentiële en de kinetische energie per eenheid van oppervlak wordt gegeven door:
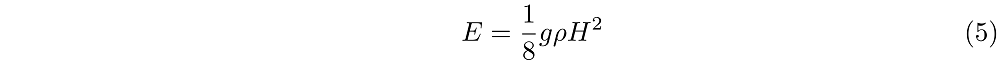
waar g weer de zwaartekrachtsversnelling, ρ de dichtheid en H de hoogte van de golf is.
Energiestroom en golfhoogte
Nu is het zo dat deze twee grootheden, de voortplantingssnelheid en de energie, samen een nieuwe grootheid vormen: de energiestroom. Dat is de hoeveelheid energie die per seconde door een golf wordt vervoerd. In formulevorm wordt de energiestroom gegeven door E n C, waarin n een waarde is die in diepe delen 1/2, en in ondiepe delen 1 bedraagt. Zolang er geen energie verloren gaat, moet de energiestroom constant blijven. Ver op zee moet die grootheid dus dezelfde waarde hebben als vlakbij de kust. Aan de hand van dat gegeven kunnen we een formule voor de hoogte van de golf opstellen. Neem daarvoor aan dat ver op zee de energiestroom wordt gegeven door E0 n0 C0, dan moet dit gelijk zijn aan de waarde bij de kust, die we schrijven als E n C. Dus: E n C = E0 n0 C0. Als we dit nu omschrijven en formule (5) invullen vinden we dat
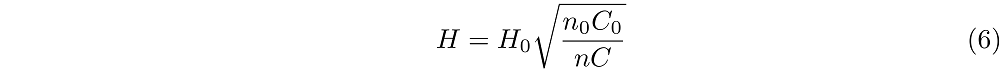
waarin we de hoogte van de golf ver op zee H0 hebben genoemd, en de hoogte dicht bij het strand H. We zien dus dat als C klein is, wat in ondiepe wateren zo is (zoals formule (4) laat zien), dat H dan groot wordt. In ondiepe wateren wordt de golfhoogte dus groter.
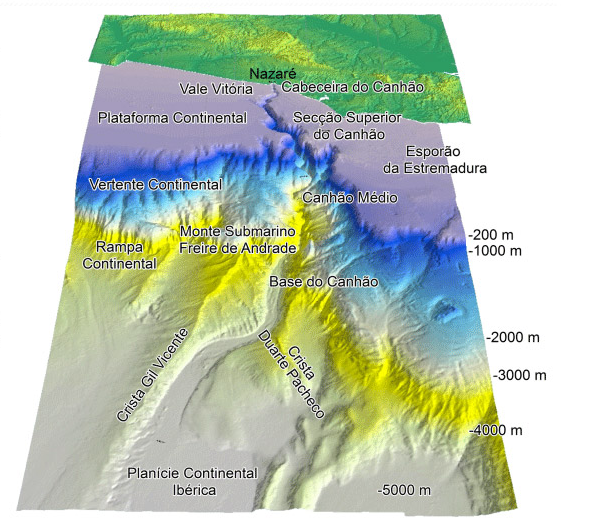
Afbeelding 3. Profiel van de zeebodem bij Nazaré.Afbeelding via Ultrawave.
Nazaré
Met behulp van deze laatste formule kunnen we een van de redenen zien hoe er bij Nazaré zulke hoge golven kunnen ontstaan. In het water voor het kustplaatsje bevindt zich namelijk een trog, een diepe kloof in de zeebodem. Zoals te zien in afbeelding 3 loopt dit onderzees ravijn in een punt helemaal naar het plaatsje Nazaré toe. Hierdoor worden ten eerste golven vanuit allerlei richtingen naar één punt, naar Nazaré, toegeleid. Daarnaast zorgt de trog ervoor dat golven binnen het ravijn tot vlakbij de kust enorme dieptes onder zich hebben. Als we naar de formules kijken die we hebben afgeleid, betekent dat dat de golven tot vlakbij de kust een enorme voortplantingssnelheid hebben. Als ze dan plotseling op de muur van het ravijn stoten, en ze zich dus plotseling in ondiep water bevinden, wordt die gigantische energie in de hoogte van de golf geïnvesteerd, zoals formule (6) uitwijst. Het plotselinge hoogteverschil in de bodemstructuur zorgt er dus voor dat de golven naar een punt worden geloosd en dat ze vlakbij Nazaré ineens al hun energie de hoogte inbrengen waardoor dus wel 30 meter hoge golven kunnen ontstaan. Reken maar dat ik dan uit het water blijf!
Afbeelding blokkenschema: Michel Mondadori.