Afbeelding 1. De gelijkenis van de talenten.Houtsnede uit 1712.
In de Bijbel, in het Evangelie volgens Matteüs om precies te zijn, staat de ‘Gelijkenis van de Talenten’. Zo’n gelijkenis is een kort verhaal waarin Jezus zijn volgelingen iets ingewikkelds probeert uit te leggen, door het met een alledaagse situatie te vergelijken. In dit geval vergelijkt hij ‘Het Koninkrijk Gods’ met een man die zijn dienaren zijn geld laat beheren terwijl hij een reis maakt. De ene dienaar krijgt vijf talenten (dat is de munteenheid), een andere krijgt twee talenten, en weer een ander krijgt één talent, ‘ieder naar wat hij aankon’.
Terwijl de eerste twee dienaren hun talenten gebruiken om handel te drijven, en zo het vermogen van hun heer verdubbelen, durft de arme stakker die slechts één talent heeft gekregen er niets mee te doen, zo bang is hij het kwijt te raken. Als de heer bij thuiskomst hierover hoort, ontsteekt hij in woede: ‘Pak hem dat talent maar af en geef het aan degene die er tien heeft. Want wie heeft zal nog meer krijgen, en wel in overvloed, maar wie niets heeft, hem zal zelfs wat hij heeft nog ontnomen worden.’
Naar deze hardvochtige Bijbelpassage is het Matteüseffect vernoemd: het fenomeen dat rijken rijker worden, en armen armer. Of, anders gezegd: hoe meer iemand al gekregen heeft, hoe groter de kans is dat hij nog iets zal krijgen. Dit effect doet zich in allerlei gebieden voor. Zo doet de Nederlandse wetenschapsfinancier NWO tegenwoordig expliciet zijn best om het Matteüseffect te voorkomen, nadat gebleken was dat diegenen die al eerder een NWO-beurs hadden gekregen een grotere kans hadden om er nog een binnen te slepen, ongeacht de kwaliteit van de aanvraag [1,2].
Ook in de netwerktheorie, het vakgebied waar ik me het afgelopen jaar mee bezig heb gehouden, speelt het Matteüseffect een grote rol. We zouden bijvoorbeeld naar een groot Twitter-netwerk kunnen kijken, waarvan je de data kunt vinden in referentie [3] onderaan dit artikel. Dit netwerk wordt gevormd door Twittergebruikers (dit zijn de knopen, of nodes van het netwerk), waarbij er een verbinding (links, in het Engels) van gebruiker A naar gebruiker B wordt gelegd als gebruiker A gebruiker B in een van zijn tweets noemt. Je kunt nu twee dingen tellen: hoe vaak gebruikers anderen noemen (dit noemen we de outdegree), en hoe vaak gebruikers door anderen genoemd worden (de indegree). Hoe deze grootheden verdeeld zijn kun je aflezen in afbeelding 2.
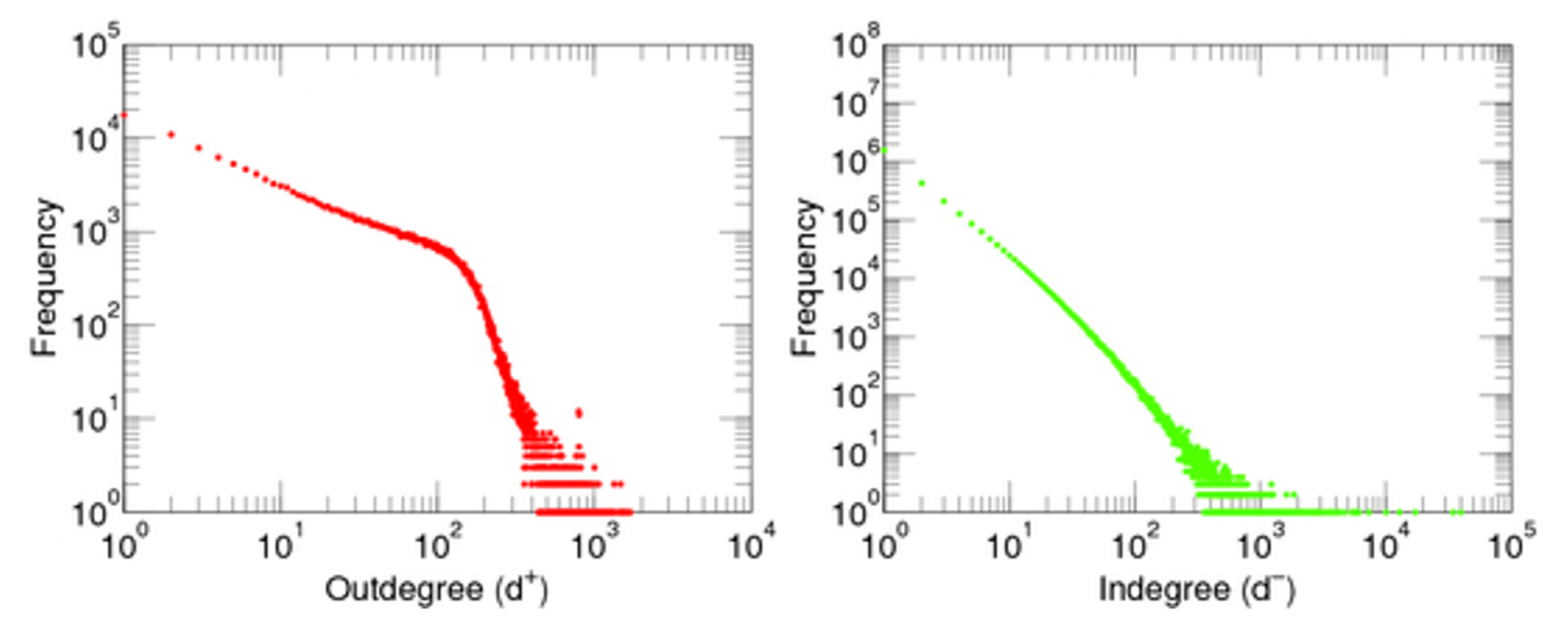
Afbeelding 2. Noemen en genoemd worden.De “outdegree” en de “indegree” van een Twitternetwerk.
Als je naar de outdegree kijkt, zie je dat er heel wat mensen zijn die maar een paar andere mensen noemen. Er zijn er ook nog flink wat die een hondertal mensen noemen. Daarna neemt de frequentie snel af, want niemand is zo gek om op Twitter meer dan tweeduizend mensen aan te schrijven. De indegree, daarentegen, is veel oneerlijker verdeeld dan de outdegree: er zijn veel meer mensen die maar heel weinig worden genoemd en ook zijn er mensen die wel duizenden keren worden genoemd, tot zelfs een paar supersterren die wel twintig- of veertigduizend keer genoemd worden.
Nog iets dat je aan de hand van de verdeling van de indegree kunt opmaken, is dat de logaritme van de indegree d haast een rechte lijn is ten opzichte van de logaritme van hoe vaak die indegree voorkomt. We duiden die frequentie met N(d) aan, en kunnen dit verband dan op twee manieren schrijven door de richtingscoëfficiënt buiten of juist binnen de logaritme te zetten:
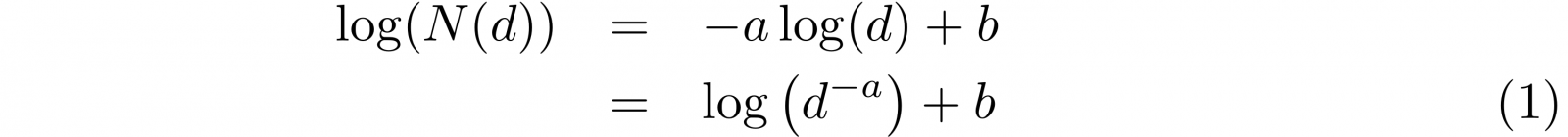
Als je van beide kanten van deze formule de e-macht neemt (we gebruiken hier de natuurlijke logaritme), zie je dat
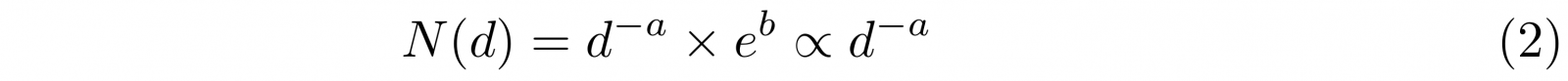
(Het symbool tussen de laatste twee uitdrukkingen betekent “rechtevenredig met”.) We zien dus dat het aantal keer dat een bepaalde indegree voorkomt als een machtswet van die indegree afhangt. Zo’n verdeling wordt ook wel een Pareto-verdeling genoemd, vernoemd naar de Italiaanse econoom Vilfredo Pareto.
Zou het Matteüseffect hier een verklaring voor kunnen geven? Leidt het feit dat populaire tweeters vaker geretweet en genoemd worden tot deze machtswet?
Om te onderzoeken hoe het Matteüseffect de verdeling van degrees in een netwerk beïnvloedt, stelden de onderzoekers Reka Albert en Albert Lázló Barabási in 1999 het inmiddels beroemd geworden Barabási-Albertmodel voor. In dit model, dat een groeiend netwerk simuleert, komen de nodes van het netwerk een voor een aan, en willen met een andere node in het netwerk een link maken. Als elke node een even grote kans zou hebben om te worden gekozen, levert dit een netwerk op waar elke node gemiddeld twee buren heeft, en waarin de degree distribution voor waardes groter dan 2 exponentieel kleiner wordt. In een loglog-plot zoals afbeelding 2 zou dat een kromme lijn betekenen, die steeds meer naar de x-as toebuigt. Geen Pareto-verdeling, dus.
Maar in het Barabási-Albertmodel wordt niet elke node wordt met een even grote kans gekozen: hoe meer verbindingen een node al heeft, hoe groter de kans om gekozen te worden. De kans Π(k) dat een node die k buren heeft gekozen wordt, is in dit model k/2N, waarbij N het totaal aantal nodes in het netwerk is. Hierin zit het Matteüseffect: een populaire node heeft een grotere kans om een nieuwe buur te krijgen. Barabási en Albert noemen dat preferential attachment. Je kunt snappen dat de noemer in de factor k/2N ervoor zorgt dat de kansen optellen tot 1, omdat er in totaal 2N buren in het netwerk zijn: er zijn namelijk N nodes, die elk een link hebben gemaakt, en elke link zorgt voor 2 buren (want de ene node is de buur van de ander, maar ook andersom). Natuurlijk is dit model een vereenvoudiging van de werkelijkheid: het is niet zo dat iedereen die aan Twitter begint slechts 1 iemand een bericht mag sturen, en dat de kans dat iemand een bericht ontvangt precies evenredig is met zijn of haar populariteit. Maar de hoop is dat dit model desondanks de gevolgen van het Matteüseffect goed beschrijft.
Tot welke degree distribution leidt dit groeiende netwerkmodel? Om daar achter te komen kunnen we gebruik maken van een zogeheten master equation. We noemen het aantal nodes met k buren op een bepaald tijdstip t daarvoor N(k,t). Als op het tijdstip t+1 een node k buren heeft, kan dat op twee manieren gebeurd zijn: de node had op tijdstip t nog k-1 buren, maar werd door de nieuwe node die op tijdstip t+1 aankwam gekozen om buren te worden (dat heeft een kans (k-1)/2N). Of deze node had al k buren, en is juist níet gekozen. Daarop is een kans (1-k/2N). We voeren nog één vereenvoudiging door, door in te zien dat het aantal nodes N gelijk is aan t, omdat er bij elke tijdstap 1 extra node bijkomt. Dan vinden we:
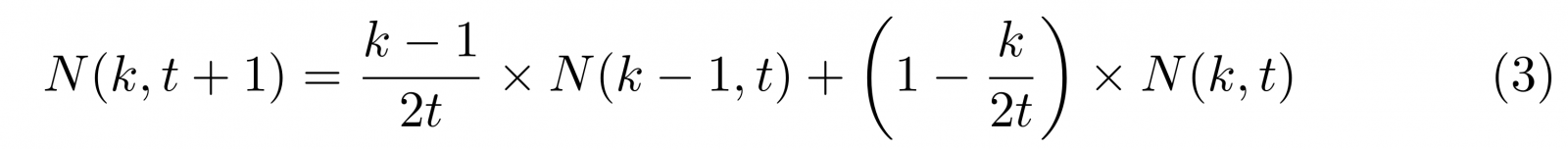
Deze vergelijking kunnen we oplossen als we aannemen dat de uiteindelijke kansverdeling P(k) van het groeiende netwerk onafhankelijk is van de tijd. Aangezien de kans om een node met k buren te vinden simpelweg gelijk is aan het aantal nodes met k buren, gedeeld door het totaal aantal nodes, dat gelijk is aan t, krijgen we P(k) = N(k,t)/t, ofwel N(k,t) = P(k)*t. Dus:
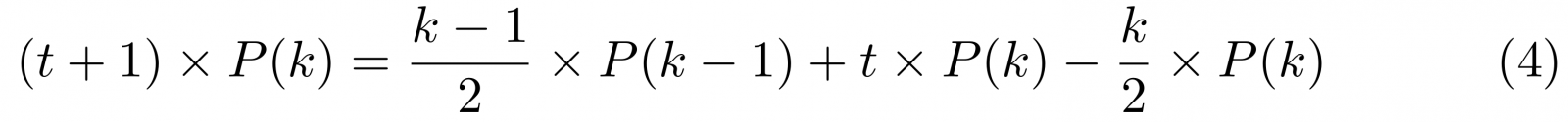oftewel
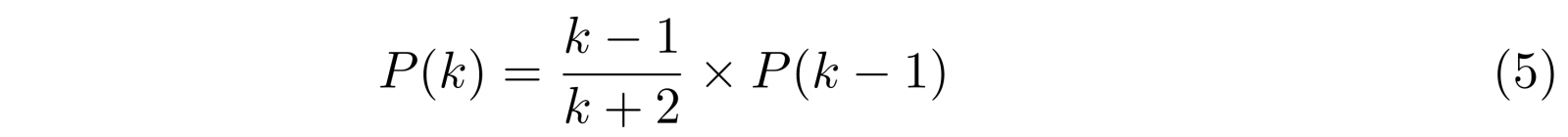
Je kan zien dat deze vergelijking de oplossing
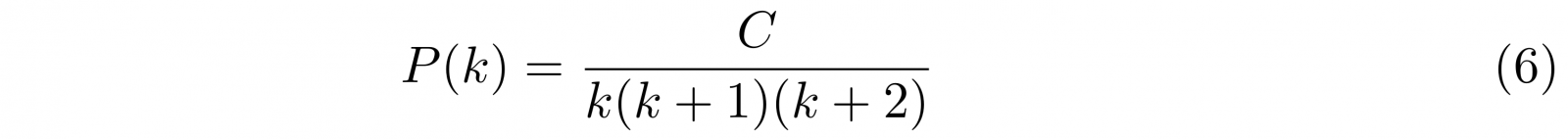
heeft, waarbij C een constante is. Dat is (ongeveer) een machtswet! De kans neemt immers grofweg af met de derde macht van k. In afbeelding 2, waar deze functie geplot is, zie je dat deze functie behoorlijk goed lijkt op wat we bij de indegree in afbeelding 2 zagen. Bovendien zie je dat de computersimulaties van het Barabási-Albert model (blauwe stippen) ook goed aansluiten bij deze voorspelling:
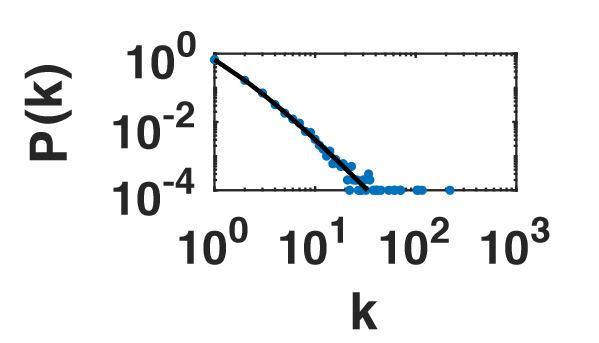
Afbeelding 3. Het model.De resultaten van het hier beschreven model, zowel als een machtswet (zwarte lijn) als in een computersimulatie (blauwe stippen). Vergelijk deze afbeelding met de groene plot in afbeelding 2.
Zo zien we dat het Matteüseffect een verklaring zou kunnen bieden voor de verdeling van indegrees in het Twitternetwerk: wie vaak genoemd wordt, heeft een grotere kans om nog eens vaker genoemd te worden, wat leidt tot een verdeling die zich als een machtwet gedraagt, een zogeheten Pareto-verdeling. Maar, misschien nog belangrijker, zien we hiermee dat er ‘natuurwetten’ achter allerlei alledaagse fenomenen schuil kunnen gaan, ook als die fenomenen geen elektronen, quarks of zwarte gaten zijn.
Meer weten over de wiskunde achter netwerken? Schrijf je dan (zie referentie [4]) in voor een de webklas “Complex Networks: small worlds with skewed distributions”, die in november van start gaat.
[3] http://konect.uni-koblenz.de/networks/munmun_twitterex_at
[4] https://www.networkpages.nl/complex-networks-an-online-course-for-dutch-high-school-students/