De krul verklaard
Over spectaculaire toepassingen hebben we het later, maar eerst de harde natuurkunde. In het filmpje hierboven wordt een alledaagse basketbal vanaf de rand van een 140 meter hoge stuwdam de diepte in gegooid. In een perfect vacuüm zou de bal ongestoord onder invloed van de zwaartekracht neerwaarts versnellen, maar de werking van de luchtdeeltjes die het ronde voorwerp in werkelijkheid tegenkomt, mag allerminst verwaarloosd worden. Die invloed is al enigszins zichtbaar als de bal de eerste maal gegooid wordt, maar wordt pas echt goed duidelijk wanneer de bal een kleine rotatie wordt gegeven. In het laatste geval is de bal systematisch onderhevig aan een horizontale kracht! Waar komt die vandaan?
Newton – wie anders – was de eerste die dit effect stelselmatig besprak, maar de naam van het magnuseffect verwijst naar de Duitse fysicus Heinrich Gustav Magnus. Zijn verklaring, die meestal beschreven wordt in het geval waarin de situatie een kwartslag gedraaid is, en een bal dus in eerste instantie horizontaal door de lucht beweegt, gaat als volgt – zie afbeelding 1. Wanneer de (basket)bal bijvoorbeeld naar rechts beweegt en, zoals in het diagram hieronder, tegen de klok in draait, zal de luchtstroom ten opzichte van het oppervlak van de bal langs de bovenzijde trager zijn dan langs de onderzijde. Het gevolg daarvan is dat de luchtmoleculen die langs de bovenkant kwamen als het ware omlaag worden meegezogen met de draairichting. De luchtdeeltjes die langs de onderkant de bal passeren, zijn juist niet geneigd de kromming van de bal te volgen, en blijven dus een eerder rechte lijn volgen na hun ontmoeting met de bal. Het netto-effect is dat de luchtstromen een neerwaartse kracht ondervinden onder invloed van het voorbijvliegend tollend object. Newtons derde wet leert ons dat een dergelijke neerwaartse kracht gecompenseerd moet worden met een even grote kracht in de tegengestelde richting. Die kracht, ditmaal op de bal onder invloed van de luchtstromen, is de netto opwaartse kracht die Magnus’ naam draagt. Exact hetzelfde mechanisme, maar dan een kwartslag gedraaid, zorgt in het videofragment voor een horizontale kracht bij een verticaal versnelde, draaiende basketbal, wat zich manifesteert als een lange krul tot in het meer.
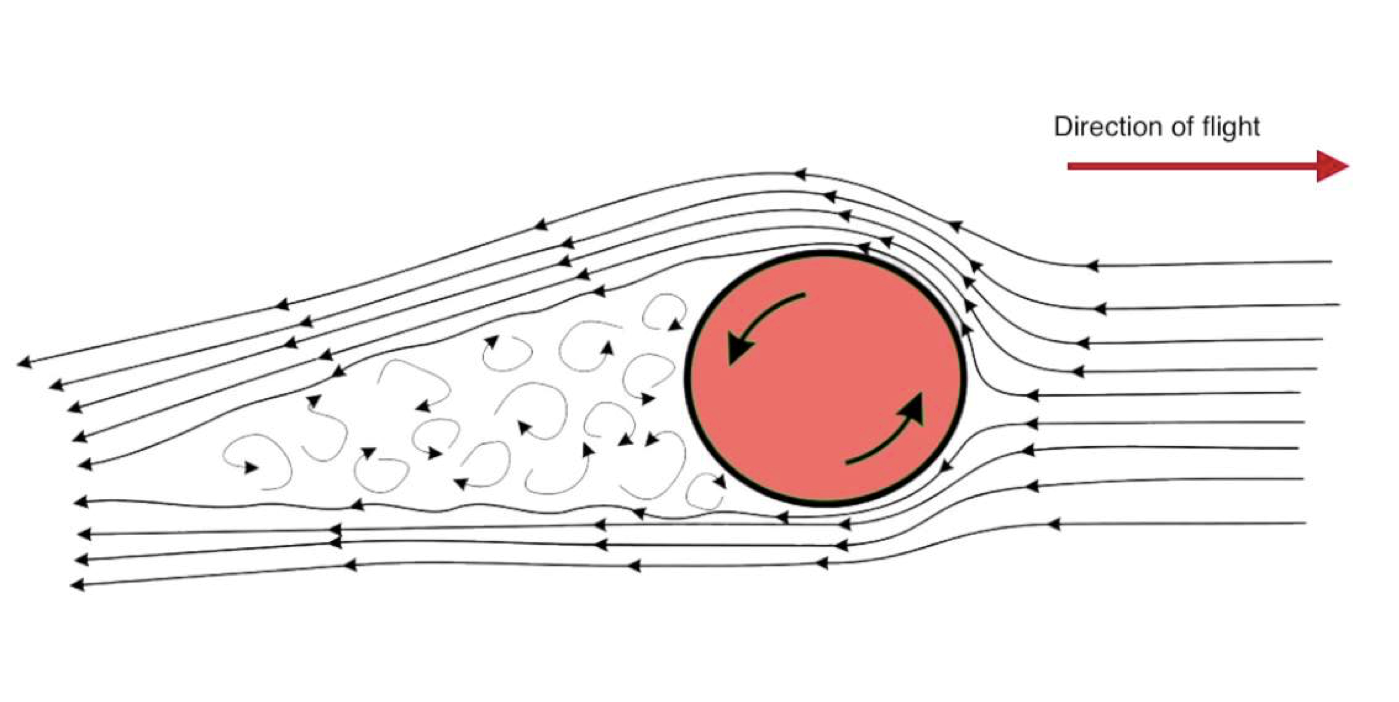
Afbeelding 1. Het magnuseffect.De luchtstromen rond een draaiend voorwerp werpen een licht op de magnuskracht. Afbeelding uit een filmpje van Fizzics.
De krullen die de krul tot stand brengen
Hoewel fysisch correct en intuïtief, gaan we met de verklaring die hierboven werd gegeven net iets te kort door de bocht. Waarom willen luchtdeeltjes de beweging van het baloppervlak volgen, en wat zijn die gekke krulletjes links naast de bal in het diagram? De doorgewinterde QU-lezer verwacht natuurlijk een grondigere natuurkundige motivatie. Immers, en met een beetje cynisme: er kleeft toch geen etherische lijm tussen de bal en de atmosferische moleculen, noch is het zelfbewustzijn van een stroom lucht sterk genoeg ontwikkeld om een bewuste keuze te maken de draaiing van een bal te volgen. Waarom dan toch de neiging van de stromen om gestuurd te worden door de draairichting? Dat heeft alles te maken met zogenaamde turbulente vortices, voorgesteld door de vermelde krulletjes. Deze vortices zijn een welbekend fenomeen in de aerodynamica en aeronautica.
Luchtstromen komen na de interactie met de bal terug samen als gevolg van het drukverschil tussen de buitenlucht en het gebied met lagere luchtdruk dat achter de gelanceerde bal ontstaat. Het samenkomen van die stromen kan evenwel bemoeilijkt worden door chaotische luchtkolkjes (de vortices) in dat “vacuüm”. Die turbulenties ontstaan meteen wanneer laagjes lucht het oppervlak van de bal verlaten. Cruciaal is dan dat het moment waarop die grenslagen van de bal loskomen, mede bepaald wordt door de snelheid waarmee de moleculen langs het object razen. Aangezien die snelheid (weer refererend naar het diagram) bovenaan lager is dan onderaan, ontstaan er vanonder eerder vortices dan aan de bovenkant. Dit is op zijn beurt weer verantwoordelijk voor het collectief neerwaarts afbuigen van alle luchtstromen, gebalanceerd door de opwaartse Magnuskracht.
Maar genoeg technische praat; hoe kan je dit fenomeen in je voordeel gebruiken?
Een magnifiek schot
Het magnuseffect is niet alleen van belang voor de bevlogen aerodynamicus; het is ook allesbehalve een geheim in verschillende balsporten. Een beroemd doelpunt van Roberto Carlos, dat bekend staat als de knapste vrije trap in de geschiedenis van het voetbal, heeft zijn faam te danken aan het effect. De waanzinnige draaiing (en snelheid) die de Braziliaan aan de bal wist te geven, zoals te zien in het filmpje hieronder, veranderde een gênante misser in een historische goal. Het effect zorgt er tevens voor dat een goed uitgevoerde hoekschop het leer toch in de winkelhaak kan afleveren. Ook (tafel)tennissers maken graag gebruik van luchtweerstand (top- of backspin), en de werper bij honkbal kan erdoor met zijn worp de slagman in de war brengen door een curveball te gooien. Het schijnt zelfs bij het paintballen gebruikt te worden om het bereik van het schot te vergroten!
Ingenieurs, aan de andere kant, hebben ook de toepassingen van het magnuseffect in hun beroep kunnen benutten. In de vaartuigkunde worden grote verticale draaiende cilinders gebruikt om op een mechanische manier te “zeilen”, wat een erg surreëel voertuig oplevert – zie afbeelding 3. Vliegtuigbouwers hebben ook al met gekke ideeën geëxperimenteerd: een horizontale cilinder vervangt eenvoudigweg de vleugels. Met voldoende rotatie en beginsnelheid, kan deze constructie het vliegtuig goed van de grond houden – zij het dat het ontwikkelen van dit systeem wel, letterlijk, met vallen en opstaan ging. Ook historische legerkanonnen maakten gebruik van een kogelomwenteling om een schot strategisch in de lucht af te buigen.

Afbeelding 2. Een rotorschip.Een schip met een zogenaamde Anton Flettnerrotor: de draaiende cilinders veroorzaken een magnuskracht die de boot voortstuwt. Foto: Wikipedia-gebruiker Carschten.
Al met al is het magnuseffect dus een erg alledaags fenomeen, maar toch een dat onwaarschijnlijke technische toepassingen heeft, en magische sportmomenten kan opleveren. Nu weet je de verrassende oorsprong!