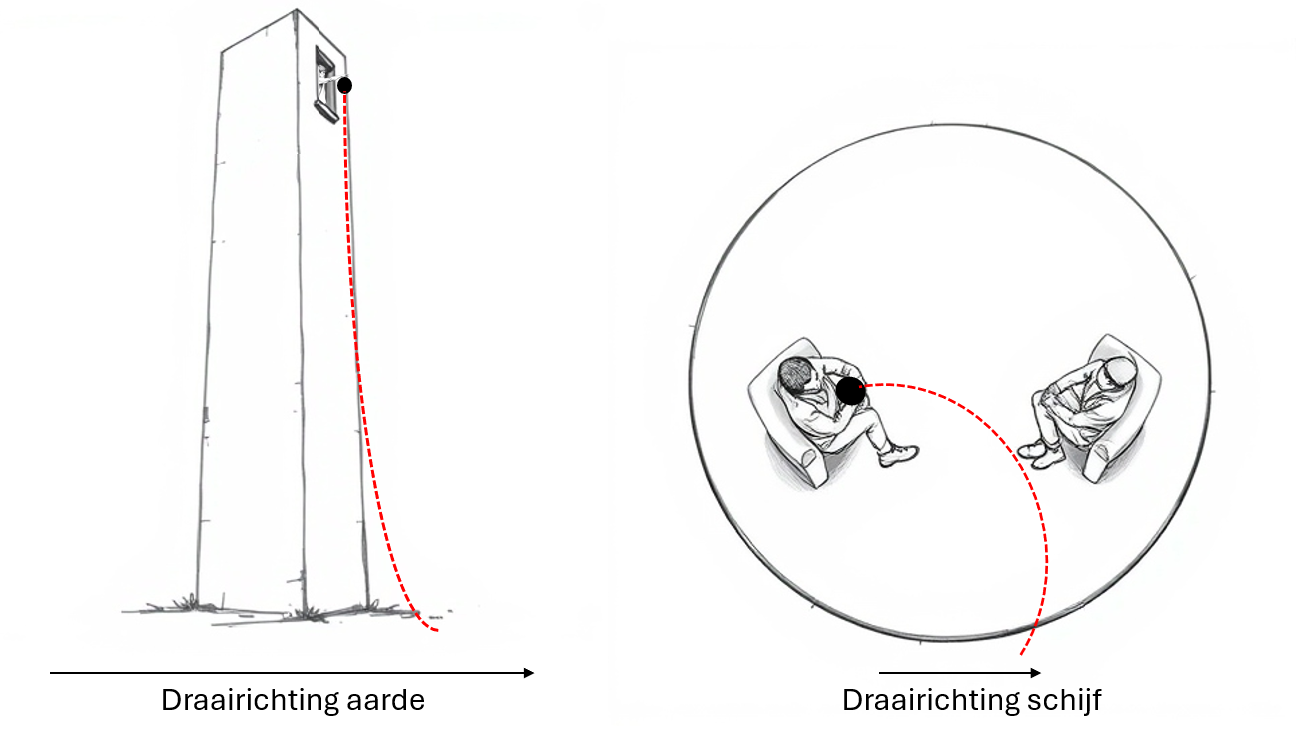
De oorzaak van het corioliseffect is dat de draaiende schijf en de aarde roteren, waardoor de tweede wet van Newton voor waarnemers die mee-roteren niet geldt. Deze wet stelt dat
\( F = ma \),
waar F de som van de krachten op het systeem (in dit geval: de bal) is, m de massa ervan, en a de versnelling van het systeem in de richting van de kracht F.
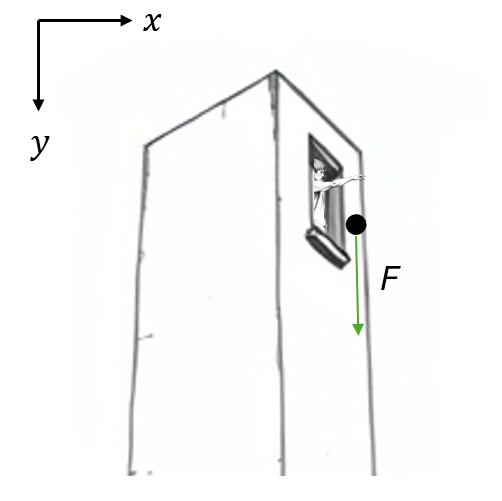
Stel dat we aannemen dat de tweede wet van Newton wél exact geldt op de draaiende aarde. Wanneer de bal bovenin de toren wordt losgelaten, werkt op deze bal de zwaartekracht \( F_Z \) in de y-richting en misschien nog de luchtweerstand \( F_L \) in de negatieve y-richting. (We kiezen die y-richting dus voor het gemak ‘omlaag’.) Netto zal er in ieder geval een positieve kracht \( F = F_Z – F_L \) in de y-richting zijn, zoals getekend in afbeelding 2. Volgens de tweede wet van Newton zorgt de kracht \( F \) ervoor dat de bal in diezelfde y-richting versnelt. Maar hoe kan het dan dat de bal zich ook in de x-richting gaat verplaatsen, zoals ik weergaf in afbeelding 1?
Het antwoord is zoals gezegd dat de tweede wet van Newton op aarde helemaal niet geldt! Deze wet is vaak een heel goede benadering van de werkelijkheid, maar helemaal exact geldt ze niet. Dit zorgt voor vreemde effecten, waar het corioliseffect een voorbeeld van is. In de volgende video wordt uitgelegd waarom de bal in het rechter plaatje van afbeelding 1 lijkt af te buigen en niet rechtdoor beweegt:
In deze video wordt ook toegelicht hoe orkanen door het corioliseffect ontstaan en op het noordelijk en zuidelijk halfrond een tegengestelde draairichting hebben.
Voor- of nadat je de video bekijkt nodig ik je uit om ook eens na te denken over de verklaring van de beweging van de bal die van de toren valt, zoals in het linker plaatje van afbeelding 1. Dit voorbeeld is heel vergelijkbaar met dat van de orkanen. Om alvast een tip te geven: de bovenin de toren vastgehouden bal heeft een grotere snelheid in de draairichting van de aarde dan de gevallen bal als die onderaan de toren ligt. De reden is dat de aarde draait en het afstand tot het middelpunt van de aarde boven en beneden de toren verschillend is.
Leuk is nu dat je de redenering ook kunt omdraaien, en we het roteren van de aarde kunnen zien door een bal uit een hoge toren te laten vallen en de afbuiging van de bal te observeren. Als je (hypothetisch gezien, doe dit alsjeblieft niet echt!) een bal uit een honderd meter hoge toren zou laten vallen, dan zal bij afwezigheid van enige wind, de afbuiging van de bal door het corioliseffect zo’n twee centimeter zijn: dit effect is zelfs meetbaar met het blote oog!
[1] Voor de lezers die bekend zijn met de slinger van Foucault: deze slinger toont aan – op vergelijkbare manier als het experiment met de bal die afbuigt als hij uit de toren valt – dat de aarde roteert en dat de tweede wet van Newton ten opzichte van het aardoppervlak niet precies geldt.