Afbeelding 1. Hardy’s paradox.Hardy’s paradox wordt besproken in een filmpje van het kanaal MinutePhysics – zie het einde van dit artikel voor het filmpje.
We bespraken op deze website al eerder het tweespletenexperiment, dat gebruikt wordt om aan te tonen dat licht zowel golf- als deeltjeseigenschappen heeft. Als we nadenken over licht in termen van golven kunnen we ons gemakkelijk voorstellen dat die golven met elkaar interfereren als ze door twee spleten gestuurd worden. Dat wordt al lastiger wanneer we over lichtdeeltjes (fotonen) spreken, en die één voor één op de twee spleten afsturen. Vanuit dat beeld is het niet zo eenvoudig om te begrijpen waarom het interferentiepatroon optreedt. De situatie wordt nog bizarder als we nu elektronen – waar we gewoonlijk over nadenken als deeltjes – gebruiken in plaats van fotonen: ook dan treedt een interferentiepatroon op.
Wat nu als we de situatie nog iets uitbreiden en niet alleen elektronen gebruiken, maar ook positronen, de ‘anti-deeltjes’ van elektronen? Dit is het idee achter het gedachte-experiment van Lucien Hardy uit 1992/1993. Het is een soort ‘dubbel-tweespletenexperiment’: we gebruiken ditmaal drie spleten, de bovenste en middelste voor onze bron van elektronen, en de middelste en onderste voor onze bron van positronen. Als we maar één van de twee bronnen aanzetten, dan verwachten we het gebruikelijke interferentiepatroon te zien achter de bovenste of onderste twee spleten. Maar wat als we beide bronnen tegelijk inschakelen?
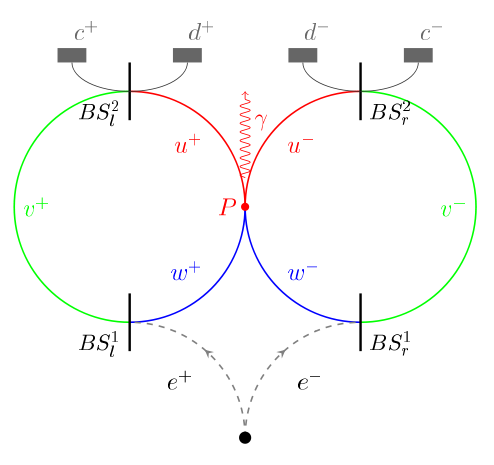
Afbeelding 2. Hardy’s opstelling.Een schets van de opstelling die Hardy in zijn oorpronkelijke artikel gebruikte. Afbeelding: Wikipedia-gebruiker Allocco.
Een experiment vergelijkbaar aan de hierboven beschreven situatie is te zien in afbeelding 1; de oorspronkelijke opstelling van Hardy’s gedachte-experiment. Zowel elektronen als positronen worden met een beam splitter (BS) gesplitst en in twee banen geleid: w– en v– voor de elektronen (e–), en w+ en v+ voor de positronen (e+). Het experiment is zo ingericht, dat als we slechts elektronen of positronen (maar niert allebei) gebruiken, die altijd terechtkomen in detector c. In tegenstelling tot eerder zijn we dus niet geïnteresseerd in een interferentiepatroon, maar simpelweg in een ‘klik’ van de detector. De c staat voor ‘constructieve interferentie’: beamsplitter BS1l zorgt er bijvoorbeeld voor dat de positronen in een quantumsuperpositie terechtkomen van positronen die langs v+ en w+ gaan; die interfereren vervolgens bij BS2l constructief met elkaar en komen eruit in c+. Hetzelfde geldt voor de elektronen, die (als er geen positronen zijn) altijd uitkomen in c–.
Voor wie bekend is met de wiskunde achter de quantummechanica (lees ook vooral verder als dat niet zo is!): we dit proces voor een enkel positron dus als volgt schrijven:
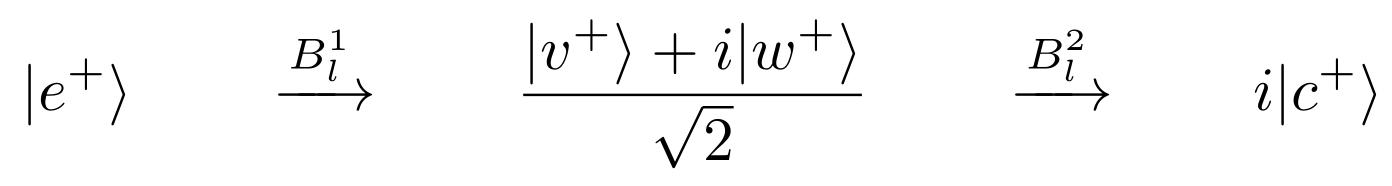
Hierin zijn de factoren i een kwestie van conventie en de factor √2 een kwestie van normalisatie. De uitdrukking zegt verder wiskundig wat we in woorden ook schreven: positronen gaan als er geen elektronen zijn langs beide banen en worden altijd gemeten in de detector c+. Evenzo worden elektronen, als de positronenbron ‘uit’ staat, altijd gemeten in c–.
Als het experiment echter gelijktijdig draait met elektronen én positronen, dan kan het gebeuren dat de baan w– van een elektron versperd wordt door een positron in w+; beide banen gaan immers door hetzelfde punt P in afbeelding 2. Klassiek gezien annihileren een elektron en positron als ze elkaar tegenkomen, en blijven er twee fotonen (γ) over. Dat betekent, als we bijvoorbeeld het elektron volgen, dat alleen het deel van de superpositie dat de baan v– volgt, aankomt in BS2r en dat blijkt weer tot gevolg te hebben dat het deeltje in beide detectoren terecht kan komen: d– én c–. Als detector d‑ dus ‘klikt’, dan kan dat alleen maar betekenen dat er een positron in de weg zat.
Weer voor de wiskundeliefhebbers: de toestand van het hele systeem, elektron én positron, is dus vóór de laatste beamsplitters bereikt worden
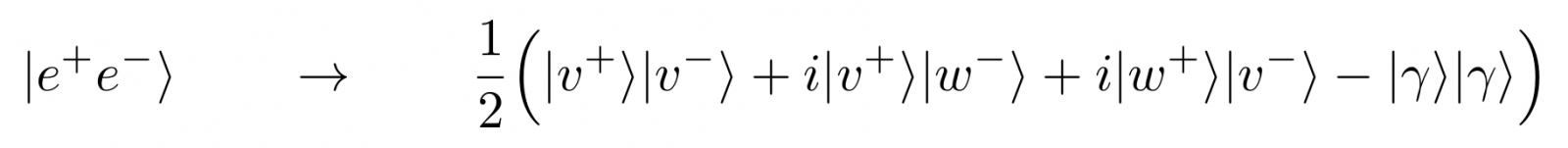
waarin de laatste term het geval weergeeft dat beide deeltjes de binnenste baan volgen en dus worden omgezet in fotonen. Welke mogelijke meetuitkomsten vinden we nu bij de detectoren? De c– en d-detectoren klikken voor respectievelijk
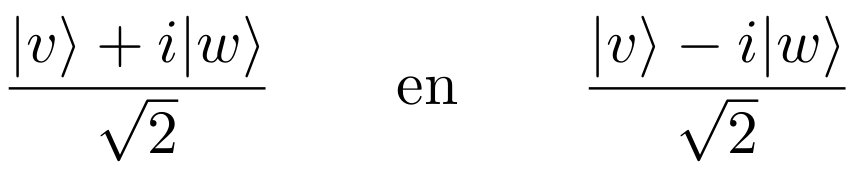
dus we kunnen de toestand hierboven ook schrijven als
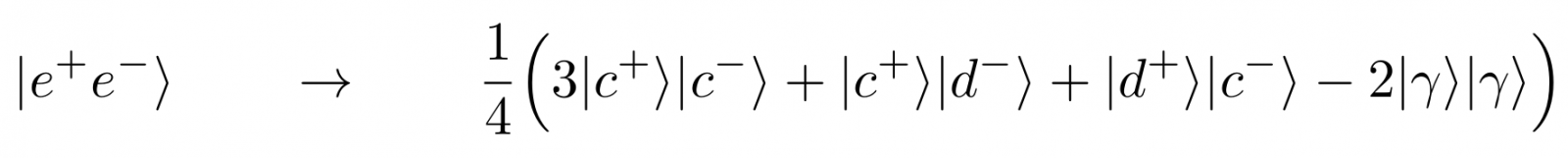
zoals je zelf kan checken door de uitdrukkingen voor c en d in te vullen.
Kon je al deze wiskunde niet volgen, dan is dat geen probleem – het resultaat waar het uiteindelijk om gaat is dat de laatste uitdrukking aangeeft dat er een bepaalde kans is (1/16, om precies te zijn) dat beide d-detectoren klikken. En daar zit ‘m de ‘paradox’: klassiek gezien concludeerden we dat de rode banen u+ en u– in afbeelding 2 niet tegelijkertijd waren toegestaan, omdat elektron en positron elkaar voor ze daar aankomen al annihileren in punt P. Het gevolg is dat we klassiek gezien nooit zouden verwachten dat beide d-detectoren klikken – dat kan hooguit één van de twee doen.
‘Echte’ experimenten tonen echter aan dat inderdaad de quantummechanische voorspelling van een detectie in d+ én d– in1 op de 16 metingen correct is! Dit is natuurlijk geen paradox – de klassieke voorspelling is simpelweg incorrect. Als de uiteindelijke meting met de detectoren c+/- en d+/- gebeurt, dan is de vraag “volgde het deeltje baan ‘u of v’” simpelweg niet goed gedefinieerd vóór die meting – beide deeltjes volgen in zekere zin beide banen, en dat is nou precies iets wat we met ons klassieke brein ons moeilijk kunnen voorstellen. Gelukkig trekt de wiskunde zich zoals je ziet zicht niets van ons beperkte voorstellingsvermogen aan, en geeft die wel het juiste antwoord.
Volkomen verward door het bovenstaande? Misschien is het dan goed om hetzelfde experiment nog eens te bekijken, maar nu zoals we het oorspronkelijk beschreven: als driespletenvariant op het tweespletenexperiment. Een dergelijke uitleg van Hardy’s paradox (waarbij de elektronen en positronen vervangen zijn door katten en anti-katten) is te vinden in het onderstaande filmpje van MinutePhysics: