Planckeenheden
Zoals we in het vorige artikel zagen, kan de lichtsnelheid gebruikt worden om de meter overbodig te maken, en afstanden uit te drukken in secondes. De lichtsnelheid wordt vaak aangeduid met de letter c, en is gelijk aan
c = 299.792.458 m/s.
De afstand tot de maan (zo’n 384.400 km) kunnen we met behulp van die constante schrijven als 1,282 seconden – de tijd die het licht erover doet om van de maan naar de aarde te reizen. Ook de eenheid “meter” hebben we dan niet meer nodig.
We kunnen nog veel verder gaan met dit “wegdefiniëren” van eenheden. Als we nog een fundamentele natuurconstante gebruiken, kunnen we op dezelfde manier ook de seconde overbodig maken. Neem bijvoorbeeld de zwaartekrachtsconstante van Newton, die vaak aangegeven wordt met de letter G. Deze constante zegt hoe groot de zwaartekracht is tussen twee massa’s van een kilogram die zich op een afstand van een meter van elkaar bevinden. De constante is ongeveer gelijk aan
G = 6,674 x 10-11 m3 kg-1 s-2.
De enthousiaste lezer kan zelf controleren dat de eenheid past bij de bovenstaande definitie. In deze formulering komt nog wel (driemaal) de eenheid “meter” voor, dus om die te verwijderen zullen we G eerst alleen moeten uitdrukken in kilogrammen en seconden door de constante drie keer door de lichtsnelheid c te delen. Het resultaat is
G/c3 = 2,477 x 10-36 s/kg.
Deze combinatie vertelt ons hoeveel seconden overeenkomen met een kilogram. We kunnen daarmee dus tijden uitdrukken in kilogrammen, en vervolgens met behulp van de lichtsnelheid afstanden ook. De afstand tot de maan, 384.400 km, oftewel 1,282 s, kunnen we door door het bovenstaande getal te delen dus ook schrijven als 5,177 x 1035 kg. De eenheid “kilogram” voor een afstand is natuurlijk erg tegenintuïtief, maar technisch gezien is er niets mis met deze uitdrukking.
Afbeelding 1. Max PlanckMax Planck (1858-1947), de Duitse natuurkundige naar wie de constante van Planck en de Planckeenheden zijn vernoemd.
Kunnen we nog een stap verder gaan en ook de laatste eenheid wegdefiniëren? Dat blijkt inderdaad te kunnen, als we nog een fundamentele natuurconstante gebruiken. Een geschikte keuze is de constante van Planck, die vaak wordt aangeduid als ћ. De precieze betekenis van deze constante wordt besproken in het artikel over quantummechanica; voor dit artikel is alleen de grootte van de constante van belang. Die is grofweg gelijk aan
ћ = 1,055 x 10-34 m2 kg s-1
We kunnen deze constante uitdrukken in alleen kilogrammen door haar te vermenigvuldigen met de lichtsnelheid en te delen door de gravitatieconstante van Newton. De uitkomst is
ћ c / G = 4,737 x 10-16 kg2.
Dit resultaat heeft de eenheid kg2, dus als we er de wortel van trekken vinden we een massa in kilogrammen. Deze massa staat bekend als de Planckmassa, mp:
mp = √(ћ c / G) = 2,177 x 10-8 kg
We hebben hiermee dus een massa-eenheid gedefinieerd die alleen is opgebouwd uit fundamentele natuurconstanten. Elke andere massa kunnen we uitdrukken in veelvouden van die massa. Als we afspreken deze Planckeenheid te gebruiken, kunnen we de eenheden dus helemaal weglaten. De afstand tot de maan, die we eerder hadden uitgedrukt in kilogrammen, kunnen we nu dus delen door de Planckmassa en schrijven als 2,378 x 1043. We hoeven nu aan dit getal geen eenheid meer toe te voegen, aangezien we de afstand hebben uitgedrukt in de “universele” Planckeenheden.

Afbeelding 2. Aarde en maanDe Aarde en de Maan gezien vanuit de Galileo-ruimtesonde. (Foto: NASA.) De afstand tussen de Aarde en de Maan is ongeveer 3,844 x 108 m. Met behulp van de fundamentele natuurconstantes c, ћ en G, kunnen we die afstand ook schrijven als 1,282 s, 5,177 x 1035 kg, of helemaal zonder eenheid (in Planck-eenheden) als 2,378 x 1043.
De redenering hierboven is via een grote omweg gegaan: we hebben de afstand tot de maan eerst uitgedrukt in meters, toen in seconden, toen in kilogrammen, en hebben die massa in kilogrammen vervolgens uitgedrukt in termen van de Planckmassa. Er is natuurlijk een kortere weg: we kunnen proberen een combinatie van c, G en ћ te vinden die een lengte in meters oplevert, en de afstand tot de maan vervolgens uitdrukken als een veelvoud van die fundamentele lengte. Met wat proberen is zo’n combinatie al snel gevonden: het is de zogenaamde Plancklengte,
lp = √(ћ G / c3) = 1,616 x 10-35 m
Als we de afstand tot de maan (3,844 x 108 m) delen door deze Plancklengte vinden we wederom dat die afstand in Planckeenheden gelijk is aan 2,378 x 1043. We hebben daarmee dus een goede check dat onze berekeningen tot nu toe kloppen.
Tenslotte kunnen we c, G en ћ ook nog combineren tot een Plancktijd:
tp = √(ћ G / c5) = 5,391 x 10-43 s
Door te delen door de Plancktijd kunnen we dus ook tijden in seconden omrekenen in tijden in Planckeenheden. Dat geldt natuurlijk ook voor de uitdrukking voor de afstand tot de maan in seconden, en ook in dit geval vinden we weer een uitkomst van 2,378 x 1043.
Samenvattend: door grootheden eerst uit te drukken in eenheden die een combinatie zijn van de eenheden “meter”, “seconde” en “kilogram”, en door die eenheden vervolgens uit te drukken in Plancklengtes, Plancktijden en Planckmassa’s, kunnen we elke grootheid uitdrukken als een getal (zonder eenheid) maal een combinatie van de Planckeenheden.
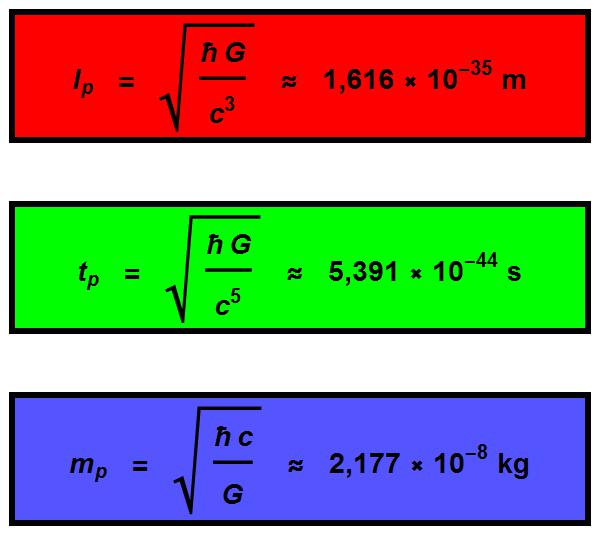
Afbeelding 6. PlanckeenhedenEen overzicht van de drie Planckeenheden. Door de zwaartekrachtsconstante (G), de lichtsnelheid (c) en de constante van Planck (ћ) op de juiste manier te combineren vinden we fundamentene lengte-, tijd- en massaschalen.
Wat is het nut van het gebruik van deze Planckeenheden? Voor de middelbare scholier die vaak vergeet eenheden te vermelden, zal het een groot voordeel lijken dat de eenheden nu weggelaten kunnen worden. Dat voordeel is echter bedrieglijk: het schrijven van eenheden is immers vervangen door het vermenigvuldigen met en delen door de juiste machten van de Planckeenheden. Het benodigde denkwerk is dus in de praktijk eerder toe- dan afgenomen. Belangrijker is dat we met de Planckeenheden een heel natuurlijke verzameling van eenheden hebben gedefinieerd: we drukken alles uit in termen van constantes die de “schaal” van de fundamentele natuur bepalen. De lichtsnelheid bepaalt bijvoorbeeld op welke snelheidsschaal de speciale relativiteitstheorie van toepassing wordt – dat is pas het geval wanneer er in experimenten snelheden bereikt worden die van de orde van grootte van de lichtsnelheid zijn. In Planckeenheden wil dat dus zeggen dat die snelheden in de buurt van het getal 1 komen te liggen – de lichtsnelheid is in Plankeenheden namelijk precies 1. Op een soortgelijke manier geeft de constante van Planck aan wanneer de quantummechanica een rol begint te spelen, en vertelt de zwaartekrachtsconstante in combinatie met de lichtsnelheid ons wanneer we ook de algemene relativiteitstheorie moeten gebruiken.
De natuurkundig interessantste situaties doen zich dus voor wanneer we een (gedachten-) experiment doen waarin alle grootheden die een rol spelen, gemeten in Planckeenheden, getallen zijn die in de buurt van 1 liggen. In dat geval hebben we voor het goed beschrijven van zo’n experiment zowel de speciale en algemene relativiteitstheorie als de quantummechanica nodig. Van de combinatie van deze theorieën begrijpen we op dit moment nog heel weinig – zie het artikel over quantumzwaartekracht voor meer daarover. Wat in elk geval duidelijk is, is dat voor het rekenen aan deze mysterieuze quantumzwaartekracht de Planckeenheden de meest natuurlijke eenheden zijn.
Zoals we aan de Planckeenheden kunnen zien, speelt de quantumzwaartekracht zich met name af op enorm kleine afstanden en tijdschalen, wanneer een betrekkelijk grote massa zich in een heel klein gebied bevindt. Dit blijkt heel duidelijk als we “alledaagse” verschijnselen in termen van Planckeenheden willen beschrijven. We zagen dat hierboven al voor de afstand tot de maan – in Planckeenheden is die afstand grofweg 2,378 x 1043 – een getal van maar liefst 44 cijfers. Ook de lengte van een mens is in Planckeenheden nog altijd een getal van 35 cijfers, en de tijd die het kost om een kopje thee te zetten is een getal van 46 cijfers. Alleen de Planckmassa lijkt niet zo extreem klein: de massa van een appel is in Planckeenheden een getal van slechts 7 cijfers. We moeten ons echter bedenken dat, om de quantumzwaartekracht een rol te laten spelen, een Planckmassa opeengepropt moet zijn in een volume van een kubieke Plancklengte, waardoor een gigantisch grote dichtheid zal ontstaan. Zo bekeken is ook de Planckmassa dus ook een extreme massa – niet extreem klein, maar juist extreem groot!