
F-theorie neemt een belangrijke plaats in in het ‘landschap van snaartheorieën’. Laten we beginnen met de naam zelf. De “F” in F-theorie zinspeelt erop dat het de vader (“father”) van alle theorieën zou zijn, een knipoog naar M-theorie, wat ook wel de moeder van de vijf verschillende snaartheorieën wordt genoemd. Maar wat is F-theorie dan precies? F-theorie is een tak van de snaartheorie, ontwikkeld door de natuurkundige Cumrun Vafa in 1996, die bepaalde configuraties in snaartheorie beschrijft op een alternatieve, meetkundige manier. De naam F-theorie kan hier dus ietwat misleidend zijn: het gaat immers niet om een op zichzelf staande theorie, maar om een duale beschrijving van een natuurkundig systeem. Dit maakt F-theorie echter niet minder interessant: het model blijkt namelijk bijzonder effectief in het construeren van semi-realistische modellen voor deeltjesfysica.
Voordat we het idee achter F-theorie kunnen begrijpen, moeten we eerst enkele essentiële ingrediënten van snaartheorie toelichten. Laten we beginnen bij één van de bouwstenen van snaartheorie – gesloten snaren. Zulke snaren zijn heel kleine lusjes die alle kanten op kunnen bewegen, en daarbij op verschillende manieren kunnen trillen. Het idee van snaartheorie is dat deze snaren de deeltjes in ons huidige model voor de natuurkunde vervangen. Dit “standaardmodel” van de natuurkunde bevat veel verschillende fundamentele deeltjes, maar er is geen verklaring voor waar al deze deeltjes vandaan komen. Snaartheorie geeft hier een verfrissende blik op: verschillende deeltjes kunnen worden beschreven door verschillende trillingen van dezelfde soort snaar.
Een van de eigenaardigheden van snaartheorie is dat het model tien dimensies nodig heeft om een consistente theorie te vormen – in tegenstelling tot de vierdimensionale wereld (drie dimensies voor ruimte en één voor tijd) die wij kennen. Om toch natuurkunde in onze werkelijkheid te kunnen beschrijven, moeten we kunnen verklaren waarom we de zes extra dimensies uit het model niet zien. Natuurkundigen bedachten hier een slimme truc voor: compactificatie. Het idee is dat de extra dimensies “klein gemaakt”, ofwel compactificeerd, kunnen worden, en daarbij zó klein worden dat we ze niet kunnen waarnemen. Neem bijvoorbeeld een vel papier. Als we dit vel heel strak oprollen en vervolgens uitzoomen, ziet het eruit als een ééndimensionale lijn, terwijl we eigenlijk met een tweedimensionaal oppervlak te maken hebben. In snaartheorie is het idee niet anders, alleen het aantal dimensies dat “opgerold” moet worden verschilt: niet één maar zes.
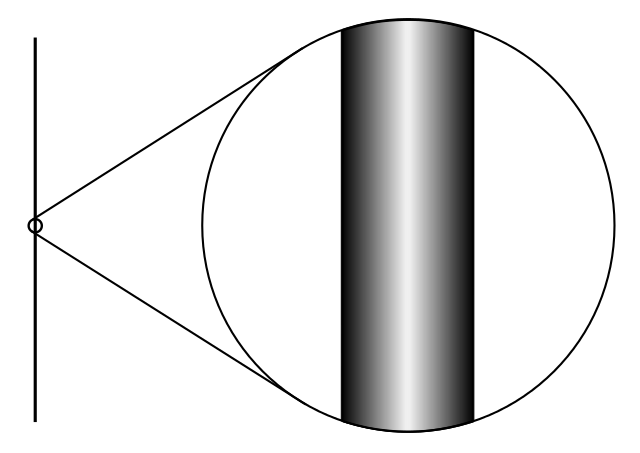
Een bijkomstigheid in dit proces is dat de extra dimensies meerdere vormen kunnen aannemen. Bij het oprollen van het vel papier kreeg de extra dimensie de vorm van een cirkel. Maar als we twee dimensies klein willen maken, kunnen we kiezen uit meerdere vormen, bijvoorbeeld een bol of een ‘donut’. Voor zesdimensionale vormen is de keuze nog vele malen groter! Dit betekent dat we op veel verschillende manieren een vierdimensionale theorie voor onze werkelijkheid kunnen maken uit een tiendimensionale snaartheorie. Nu blijkt dat de keuze voor de ‘oprolvorm’ ook erg belangrijk is, omdat iedere keuze voor een ander soort deeltjes in onze vierdimensionale wereld zorgt. In de praktijk maakt dit het wel erg lastig om snaartheorie te testen, omdat we er nog niet achter zijn welke van de vele vormen leidt tot de deeltjes die wij zien.
Hoe past F-theorie in dit verhaal? F-theorie geeft ons een alternatieve beschrijving voor de zogenaamde ‘Type IIB-snaartheorie’, één van de vijf verschillende snaartheorieen. Het blijkt namelijk dat deze snaartheorie er heel opmerkelijk uitziet: de tiendimensionale theorie heeft zelf veel weg van een twaalfdimensionale theorie die gecompactificeerd is, waarbij de twee extra dimensies eruit zien als een heel kleine donut, of netter gezegd, een torus. Een handige manier om hierover na te denken is door ons voor te stellen dat er aan ieder punt van de ruimtetijd van snaartheorie zo’n torus is vastgeplakt. Deze manier van denken is vooral nuttig als er naast de eerder genoemde gesloten snaren ook open snaren (met twee eindpunten) in ons model aanwezig zijn; het blijkt dan dat de torus er niet meer op ieder punt hetzelfde uit hoeft te zien!
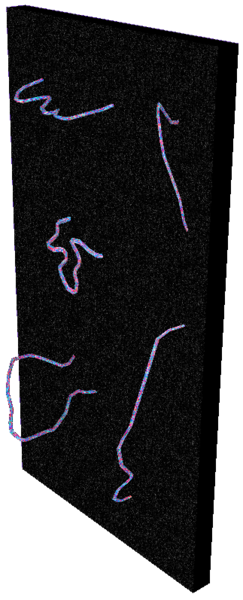
Laat ik eerst uitleggen hoe open snaren precies werken. Een open snaar heeft twee uiteinden, dus dat leidt al snel tot de vraag: zitten deze uiteinden ergens aan vast? Het antwoord blijkt ja te zijn, en de “membranen” waar deze snaren aan vast zitten worden D-branen genoemd. In de afbeelding hierboven is een tweedimensionale D-braan afgebeeld, ook wel D2-braan genoemd: een oppervlak waar de snaren op kunnen eindigen. Wat is nu het nut van deze D-branen? Het toevoegen van D-branen blijkt erg belangrijk te zijn voor het soort deeltjes dat in ons model kan voorkomen. De trillingen van de bijbehorende open snaren zien wij namelijk als deeltjes zoals fotonen en gluonen. Dit soort deeltjes is onmisbaar voor de werking van elektromagnetisme en de kernkrachten.
In het geval van F-theorie blijkt nu dat de fictieve torus zich erg bijzonder gaat gedragen wanneer er zevendimensionale D-branen, D7-branen, aanwezig zijn. Zonder D7-branen ziet de torus er op ieder punt van de onderliggende ruimte hetzelfde uit. Maar wanneer we in de buurt van D7-branen komen, vervormt de torus zich. Sterker nog, de torus knijpt zich samen wanneer we op de plek van een D7-braan komen. Dit betekent dat we nu in plaats van de D7-branen zelf, ook dit soort samenstellingen kunnen bekijken: vormen waarbij aan ieder punt een torus is “vastgeplakt”. We hoeven dus niet meer alle mogelijke opstellingen van D7-branen te onderzoeken om naar de deeltjes in ons standaardmodel te zoeken, maar we kunnen in plaats daarvan deze samengestelde vormen bestuderen.
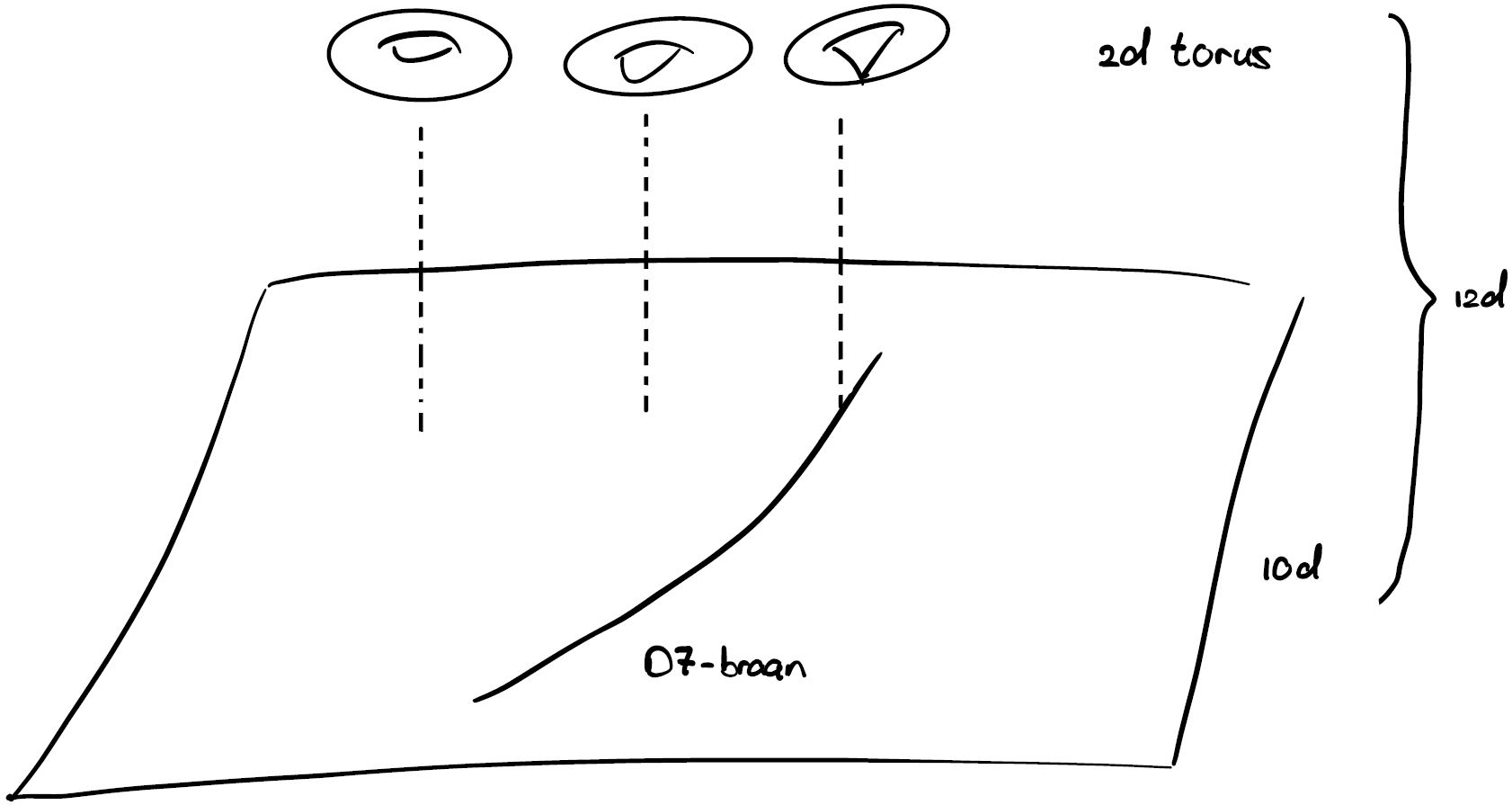
Wat nu blijkt is dat dit soort samengestelde vormen al grondig bestudeerd zijn door wiskundigen. Zo hebben wiskundigen al geclassificeerd op wat voor manieren een torus zich kan samenknijpen, oftewel: hoe die torus zich gedraagt in de buurt van wat natuurkundigen D7-branen noemen. Iedere klasse in deze classificatie blijkt overeen te komen met bepaalde deeltjes die voortkomen uit de trillingen van de open snaren op de D7-branen. Zo kunnen we bijvoorbeeld aan het gedrag van de torus zien of we met de fotonen van elektromagnetisme, of de gluonen van de sterke kernkracht te maken hebben. De overeenkomsten gaan echter verder dan dit: we kunnen ook de sterkte van interacties tussen deeltjes bepalen uit meetkundige data van de samengestelde vorm, en nog veel meer! Dit maakt F-theorie tot een zeer interessante methode om vanuit snaartheorie modellen voor deeltjesfysica te maken. Recent zijn snaartheoreten er zelfs in geslaagd om via F-theorie op een quadriljoen (een getal met 15 nullen!) aan verschillende manieren de deeltjes in ons standaardmodel na te maken. (Een populairwetenschappelijk artikel over dit onderzoek is hier te vinden.) Welke van die constructies overeenkomt met onze natuurkunde is alleen helaas nog steeds een mysterie.
De oorspronkelijke hoop was dat men erachter kon komen hoe de twaalfdimensionale theorie er nu precies uitziet, en deze theorie zou dan F-theorie zijn. Tot nog toe zijn natuurkundigen dáár niet in geslaagd. Sterker nog, ze hebben aangetoond dat supersymmetrie, een symmetrie die deeltjes in een theorie met elkaar associeert, niet in theorieën met meer dan elf dimensies kan bestaan. En deze supersymmetrie is nou juist cruciaal in het formuleren van snaartheorie. F-theorie is daarmee dus geen volledige twaalfdimensionale ‘theorie’ in de gebruikelijke zin van het woord; het is een twaalfdimensionale meetkundige manier om configuraties in de snaartheorie te ‘vertalen’. Gelukkig kwamen snaartheoreten erachter dat ook F-theorie via de overkoepelende M-theorie bestudeerd kan worden, waardoor het toch mogelijk is om deze wiskundige aanpak in het breedst mogelijke kader toe te passen.
Kortom, F-theorie geeft ons een interessante methode om deeltjesfysica na te bootsen in snaartheorie. Op het eerste oog lijkt deze alternatieve beschrijving misschien onnodig ingewikkeld, omdat men eerst nóg twee extra dimensies moet introduceren, en snaartheorie heeft al zes dimensies meer nodig. Aan de andere kant blijkt dit juist dé manier om de snaartheorie onder controle te krijgen. F-theorie toont ons hoe we ingewikkelde natuurkundige modellen beter kunnen begrijpen door de kracht van de meetkunde.