
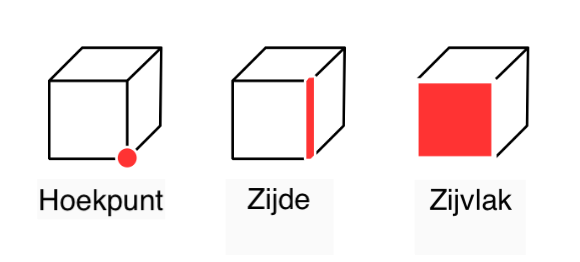
Dobbelstenen zijn er in een verscheidenheid aan vormen. De meest gebruikelijke vorm is de kubus, maar afhankelijk van het spel kom je soms ook andere, meer exotische vormen tegen. Binnen de wiskunde staan deze verschillende vormen bekend als veelvlakken of polyeders. Een veelvlak is een driedimensionaal object dat begrensd wordt door een eindig aantal veelhoeken. Deze veelhoeken worden ook wel zijvlakken genoemd, en de lijnstukken waar de zijvlakken samenkomen heten de ribben. Tot slot noemen we de punten waar de lijnstukken elkaar raken de hoekpunten van het veelvlak. Voor wie visueel is ingesteld – en deze wiskundige definitie graag in plaatjes voor zich ziet – is het handig om een specifiek veelvlak in gedachten te hebben, bijvoorbeeld een kubus of een piramide. In afbeelding 2 is voor de kubus aangeven wat we precies bedoelen met de concepten hoekpunt, ribbe en zijvlak.
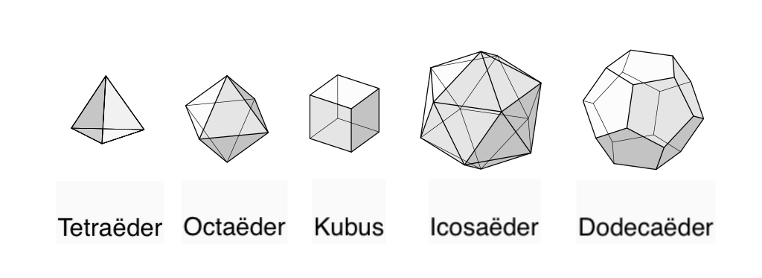
Een interessante verzameling van veelvlakken zijn de platonische lichamen. Er is een totaal van vijf van zulke regelmatige veelvlakken, afgebeeld in afbeelding 3. Het bekendste platonische lichaam is de kubus, maar als je goed zoekt kun je de andere ook terugvinden tussen de dobbelstenen in afbeelding 1. Deze regelmatige veelvlakken waren al in de oudheid bekend, en zijn sindsdien uitgebreid door wiskundigen bestuurd. Ze spelen onder andere een belangrijke rol in de filosofie van Plato, en worden daarom ook ‘platonische lichamen’ genoemd. Er zijn veel interessante dingen te zeggen over de regelmatige veelvlakken, maar voor nu richt ik me op een ogenschijnlijk toevallige eigenschap die ze alle vijf gemeen hebben.
Gegeven een veelvlak is het niet ingewikkeld om het aantal hoekpunten, ribben en zijvlakken te tellen. We geven het aantal hoekpunten aan met de letter \( V \), het aantal ribben met \( E \) en het aantal zijvlakken met \( F \). In het Engels worden de termen ‘hoekpunt’, ‘ribbe’ en ‘zijvlak’ vertaald naar ‘vertex’, ‘edge’ en ‘face’, vandaar dat het gebruikelijk is de bovengenoemde letters te gebruiken. Met wat denkwerk kun je voor ieder platonisch lichaam deze aantallen tellen. Voor de kubus geldt bijvoorbeeld \( V = 8, E = 12, F = 6 \). Er is nu iets bijzonders aan de hand: als we het aantal hoekpunten en het aantal zijvlakken van een regelmatig veelvlak bij elkaar optellen, en daar vervolgens het aantal ribben van aftrekken, is het resultaat altijd gelijk aan twee. Hoewel de afzonderlijke getallen voor iedere vorm verschillend zijn, blijkt deze specifieke berekening altijd hetzelfde antwoord te geven – een feit dat laatst ook al even voorbijkwam in dit artikel van Alexander van Spaendonck.
Het blijkt dat de wonderlijke manier waarop de getallen tegen elkaar wegvallen in de formule geen toeval is! Euler was in staat om deze uitspraak te bewijzen voor een grotere groep van veelvlakken. De extra eigenschap die Euler nodig had was dat het veelvlak convex moet zijn. Wiskundig betekent dit het volgende: als je twee punten op het veelvlak neemt, moet het lijnstuk tussen beide punten ook volledig binnen het veelvlak vallen. Grofweg komt het er dus op neer dat de dobbelsteen in het inwendige geen ‘gaten’ mag hebben. Met zijn bewijs kwam Euler uit op de formule die ik hierboven al in woorden beschreef:
\(V – E + F = 2\\
\)
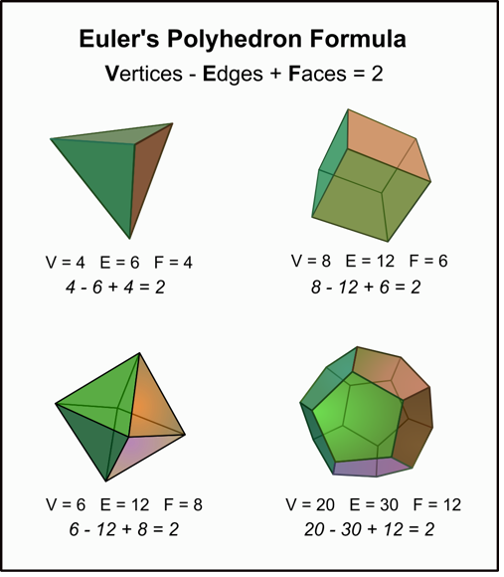
Dit resultaat staat tegenwoordig bekend als de formule van Euler. Het is een leuke opgave om de formule na te gaan in het geval van de andere platonische lichamen. In afbeelding 4 is deze berekening voor een aantal van deze regelmatige veelvlakken weergeven.
Een echt goed begrip van waarom deze formule werkt – en dus geen toeval is – kwam eigenlijk pas veel later. De specifieke combinatie \( C = V – E + F \) blijkt een voorbeeld te zijn van een topologische invariant. Zoals al eerder besproken in andere artikelen (zie bijvoorbeeld dit artikel) is topologie de wiskundige theorie van vormen. Het blijkt dat je binnen deze theorie voor iedere vorm een getal kunt uitreken dat hetzelfde blijft als je het object vervormt zonder te knippen of te klappen. Zo’n getal noemen we een topologische invariant. Verrassend genoeg kun je een topologische invariant definiëren die in het geval van een veelvlak reduceert tot de formule voor \( C \) in termen van het aantal hoekpunten, ribben en zijvlakken. Met de formule van Euler als inspiratiebron wordt deze topologische invariant ook wel de Eulerkarakteristiek genoemd.
Het feit dat alle convexe veelvlakken tot hetzelfde antwoord leiden, komt nu simpelweg doordat al deze veelvlakken dezelfde topologie – oftewel: dezelfde globale vorm – hebben. Binnen de topologie zijn de kubus, piramide en andere convexe veelvlakken allemaal om te vormen tot een bol. Om een ander antwoord voor \( C \) te krijgen dan twee, moet je een veelvlak maken dat een andere globale vorm heeft dan de bol, bijvoorbeeld door de hoekpunten en ribben van het veelvlak op een donut te tekenen. Probeer het vooral zelf: als je het goed doet kom je dan uit op \( C = 0 \).
De formule van Euler en de latere generalisatie naar algemenere vormen hebben een belangrijke rol gespeeld binnen de wiskunde. Ook in de natuurkunde kom je de Eulerkarakteristiek vaak tegen, bijvoorbeeld in de snaartheorie. Het voert te ver om dit in meer detail uit te leggen, dus ik laat deze interessante natuurkunde voor een volgend artikel. Voor nu hoop dat dit artikel een glimp heeft laten zien van de wiskunde die schuilgaat achter alledaagse dingen – in dit geval de vorm van een dobbelsteen.