Entropische zwaartekracht en donkere materie

Zwarte gaten

In 1975 kwam Stephen Hawking [1] tot de verrassende ontdekking dat zwarte gaten warmtestraling uitzenden. Hij berekende, voortbordurend op eerder werk van Jacob Bekenstein [2], dat zwarte gaten zowel een temperatuur als een entropie hebben. De entropie van zwarte gaten blijkt gelijk te zijn aan een kwart van het oppervlak A van de waarnemingshorizon  gemeten in Planckse eenheden. De precieze formule (inclusief constante van Boltzmann k_B) luidt

S = k_BA/4l²

waarbij de oppervlakte-eenheid gelijk wordt genomen aan het kwadraat van de Plancklengte

l² = ћG/c³= 10^-68 m²

met c de lichtsnelheid, G de gravitatieconstante en ћ de gereduceerde constante van Planck. De temperatuur van een zwart gat wordt bepaald door de gravitationele versnelling g bij de horizon (berekend via de wet van Newton) met

k_BT = ћg/2πc.

De ontdekking van Hawking markeert het begin van een verwoed debat over de vraag hoe zwarte gaten kunnen verdampen zonder dat de informatie over de oorspronkelijke quantumtoestand (van waaruit het zwarte gat is ontstaan) verloren gaat. Dit probleem staat bekend als “de informatie-paradox”.

Snaartheorie

De tweede theoretische ontwikkeling heeft te maken met de snaartheorie. De snaartheorie was eind jaren zestig aanvankelijk ingevoerd als mogelijke beschrijving van de sterke interactie in hadronen en mesonen. Maar in 1976 kwamen Joël Scherk en John Schwarz [3] met het verrassende voorstel dat, met wat kleine aanpassingen, de snaartheorie opgevat kan worden als een quantumtheorie van gravitatie. In de jaren tachtig werd de snaartheorie, voornamelijk door het werk van Michael Green, John Schwarz en Edward Witten [4], algemeen omarmd als een veelbelovende “theorie van alles”. Toen werd duidelijk dat alle fundamentele krachten en elementaire deeltjes in de snaartheorie beschreven kunnen worden.

Maar niet iedereen was overtuigd. Met name Gerard ’t Hooft [5] liet zich kritisch uit over de snaartheorie en vond onder andere dat de aannames van supersymmetrie en het bestaan van extra dimensies de theorie nodeloos ingewikkeld maakten. Hij benadrukte dat een quantumtheorie van gravitatie pas volledig werkt als deze ook in staat is zwarte gaten te beschrijven en de entropie-formule van Bekenstein en Hawking te reproduceren. Bovendien moest een theorie van quantumgravitatie kunnen verklaren hoe zwarte gaten kunnen verdampen zonder informatie te verliezen.  Zo’n microscopische beschrijving van zwarte gaten lag echter ver buiten het bereik van de snaartheorie zoals die aanvankelijk was opgesteld. Het (te) simpele idee dat deeltjes kunnen worden voorgesteld als trillende snaartjes bleek niet toereikend, omdat daarmee slechts storingsrekening kan worden gedaan.

De grote verandering kwam in het midden van de jaren negentig met de  “tweede snaarrevolutie”. Toen bleek dat de  snaartheorie, naast trillende snaartjes, nog meer objecten bevat: zogenaamde D-branen. Dit zijn uitgebreidere objecten, membranen met twee of meer dimensies waarlangs  de snaren kunnen bewegen. Bovendien vonden snaartheoreten methodes om berekeningen te doen die verder gingen dan storingstheorie. Al snel werd duidelijk dat het hierdoor wel mogelijk werd om zwarte gaten te beschrijven in de taal van de snaartheorie, en ook om hun entropie te berekenen. Die berekening werd voor het eerst gedaan voor een speciaal soort zwarte gaten (supersymmetrische zwarte gaten, met lading) door Andrew Strominger en Cumrun Vafa [6]. Het is een van de meest opvallende resultaten, zeg maar gerust een van de “wonderen van de snaartheorie”, dat het resultaat precies overeenkomt met de Bekenstein-Hawking formule. 

Een volgende doorbraak liet niet lang op zich wachten. De microscopische beschrijving van zwarte gaten bleek namelijk geen gebruik te maken van de aanname van het bestaan van zwaartekracht. Het was een belangrijke inzicht van Juan Maldacena [7] dat er een precieze vertaling te maken is tussen de microscopische beschrijving (zonder zwaartekracht) en de macroscopische beschrijving met zwaartekracht. De afbeelding blijkt ‘holografisch’ te zijn in de zin dat de microscopische beschrijving geldt voor de rand van de ruimte waarin de macroscopische gravitationele theorie. 

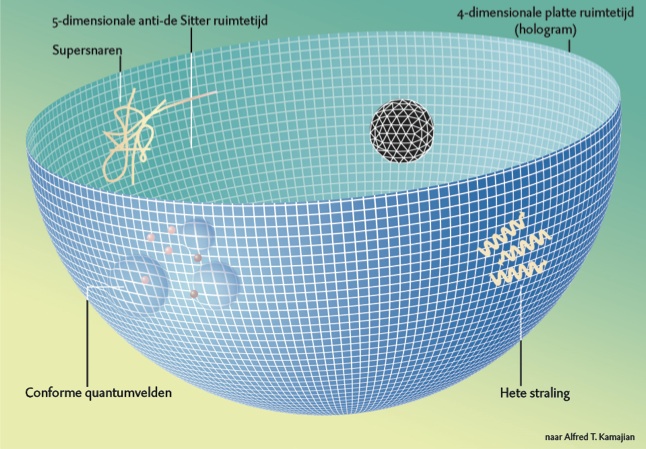
Afbeelding 1. AdS/CFT.
De anti-de Sitter-conforme veldentheoriecorrespondentie, of kortweg AdS/CFT, is een equivalentie tussen een conform invariante ijktheorie in vier dimensies (zonder gravitatie) met een volledige superstringtheorie in tien dimensies. Vijf van deze dimensies komen overeen met een anti-de Sitterruimte, waarvan de rand de vierdimensionale ruimte voorstelt waarin de ijktheorie leeft. Zwarte gaten in de anti-de Sitterruimte worden in de ijktheorie beschreven als een thermische toestand met een hoge entropie. 

Inmiddels zijn we bijna twee decennia verder. Deze tussenliggende periode is vooral besteed aan het uitwerken van de nieuwe inzichten die de tweede snaarrevolutie hadden opgeleverd. De meeste aandacht is blijven uitgaan naar de holografische correspondentie van Maldacena. Het enthousiasme hiervoor is gemakkelijk te verklaren. De microscopische theorie komt overeen met een ijktheorie, vergelijkbaar met het Standaardmodel, maar dan supersymmetrisch en conform invariant. De andere kant van de correspondentie ziet er bij lage energie uit als een (super-)gravitatie in een negatief gekromde ruimte-tijd: de anti-de Sitter-ruimte. De correspondentie tussen de conform invariante ijktheorie en de supergravitatietheorie in anti-de Sitter-ruimte, kortweg AdS/CFT genoemd, legt een verband tussen de verschillende fundamentele wisselwerkingen in de Natuur: de ijk-interacties en gravitatie. 

Het meest interessante aan de AdS/CFT correspondentie is dat het zwaartekracht te voorschijn laat komen vanuit een microscopische beschrijving zonder gravitatie. Met andere woorden zwaartekracht is emergent. Het is alleen spijtig dat de anti-de Sitter-ruimte, waarin de zwaartekracht te voorschijn komt, weinig lijkt op het heelal waarin wij zelf leven. Een anti-de Sitter-ruimte is een oplossing van de Einstein-vergelijkingen met negatieve kosmologische constante, terwijl ons universum een positieve kosmologische constante nodig heeft om de versnellende uitdijing van het heelal te verklaren. 

Entropische zwaartekracht

Vijf jaar geleden kwam ik op het idee om de inzichten verkregen uit de bestudering van zwarte gaten te combineren met de lessen vanuit de snaartheorie. Al in de jaren negentig had Ted Jacobson [8] laten zien dat de Einstein-vergelijkingen kunnen worden afgeleid uit de wetten van de thermodynamica, wanneer je uitgaat van het holografisch principe. Maar ik wilde beter begrijpen waarom entropie en temperatuur een rol spelen binnen de zwaartekracht. 

Het is een bekend verschijnsel in systemen met veel vrijheidsgraden, zoals polymeren of colloïden, dat veranderingen van entropie leiden tot een kracht. Een dergelijke emergente kracht wordt een “entropische kracht” genoemd. Mijn nieuwe inzicht was dat zwaartekracht net zoals een entropische kracht wordt veroorzaakt door veranderingen in entropie. De verandering in entropie die aanleiding geeft tot de gravitatie heeft echter niets te maken met de aanwezigheid van deeltjes met een eindige temperatuur (zoals bij gassen of colloïdale vloeistoffen het geval is). De entropie die verantwoordelijk is voor gravitatie moet worden opgevat als een maat voor de hoeveelheid quantuminformatie; dit is informatie die nodig is om de precieze microscopische quantumtoestand van de lege ruimte, dus zonder deeltjes, te beschrijven. Het feit dat informatie kan worden gemeten door een entropie is bekend uit de informatietheorie en wordt de Shannon-entropie genoemd. Bijvoorbeeld, informatie die kan worden opgeslagen in N bits draagt een Shannon-entropie gelijk aan

S = log 2^N

Voor quantuminformatie bestaat er een soortgelijke definitie in termen van het aantal qubits. 

Door aan te nemen dat deze microscopische informatie in hoeveelheid overeenkomt met de Bekenstein-Hawking entropie-formule, kon ik op opvallend eenvoudige manier de wetten van Newton afleiden. Zowel de traagheidswet als de gravitatiewet 

F = GMm/r²

volgen na een paar kleine stappen. Deze nieuwe kijk op het ontstaan van gravitatie uit verandering van entropie wordt “entropische zwaartekracht” genoemd. 

Sinds het verschijnen van het artikel “On the origin of gravity and the laws of Newton” [9] in 2010 zijn er steeds meer onderzoekers overtuigd geraakt dat zwaartekracht te voorschijn komt uit microscopische quantuminformatie. Met name het laatste jaar is deze ontwikkeling in een stroomversnelling geraakt, waarbij begrippen als quantumverstrengeling en de bijbehorende verstrengeling-entropie een centrale rol spelen. 

Waarnemingshorizon

Maar wat levert dit ons op? Sowieso kan men zich afvragen hoe een theorie van quantumgravitatie ooit van belang kan zijn voor experimentele waarnemingen. De lengteschaal waarop quantumeffecten in gravitatie plaatsvinden, de Planckschaal, is immers zo klein, en de bijbehorende energieschaal zo groot, dat we daar met geen enkele deeltjesversneller ooit bij in de buurt zullen komen. Tot voor kort was het antwoord dat quantumgravitatie pas nodig is om te beschrijven wat er gebeurt bij singulariteiten in de ruimte-tijd, zoals in het centrum van zwarte gaten of op het moment van de oerknal. 

Dit beeld is aan het veranderen. De discussies over de informatie-paradox bij zwarte gaten hebben duidelijk gemaakt dat de algemene relativiteitstheorie al niet meer goed werkt in de buurt van een waarnemingshorizon, nog ver weg van de singulariteit. Dergelijke horizons kunnen vreselijk groot zijn, en de kromming van de ruimte nog onmerkbaar klein. Waarnemingshorizons treden bovendien niet alleen op bij zwarte gaten. Ook in de kosmologie bestaan er dergelijke horizons. 

In een uitdijend heelal wordt de snelheid waarmee een punt op afstand R van ons vandaan beweegt bepaald via de wet van Hubble

v =  HR.

De kosmologische waarnemingshorizon bevindt zich op die straal R_H waar de uitdijsnelheid gelijk wordt aan de lichtsnelheid. Als we voor het gemak even aannemen dat H een constante waarde heeft, dan ligt de horizon op een afstand 

R_H = c/H.

In ons universum is juist de meeste energie aanwezig in de vorm van donkere energie: volgens het huidige kosmologische model is dat 70%. Een heelal met enkel donkere energie komt overeen met een de Sitter-ruimte met een Hubble constante H die wordt bepaald door de donkere energiedichtheid ρ_Λ via de Friedmann-vergelijking

H² = 8π Gρ_Λ /3.

Net als bij zwarte gaten kan er een entropie en een temperatuur worden toegekend aan deze kosmologische horizon. Deze voldoen ook aan de formules van Bekenstein en Hawking. Als we de huidige waarde H₀  van de  Hubble constante gebruiken, dan vinden we een entropie van 10¹²⁰. Dit is onvoorstelbaar groot. De Sitter-ruimte moet dus worden opgevat als een ruimte met een enorme entropie. 

De temperatuur wordt net als bij zwarte gaten bepaald door de versnelling bij de horizon 

k_BT =  ћg_H/2πc

waarbij  

g_H  = cH.

Het belang van dit resultaat zal zo duidelijk worden. 

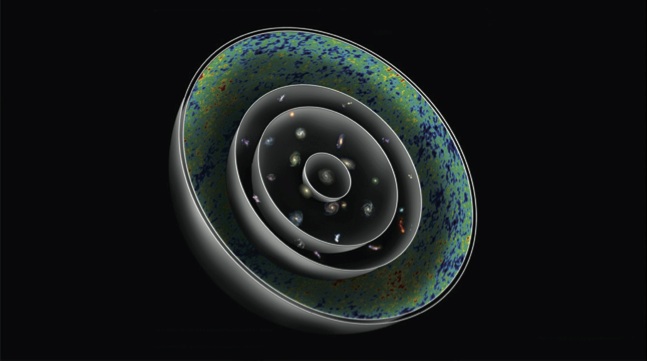
Afbeelding 2. Zichtbare heelal.
De grootte van het zichtbare heelal wordt bepaald door de snelheid van de Hubble-expansie. De kosmische achtergrondstraling komt van het verst afgelegen deel dat nog waarneembaar is. De kosmologische horizon ligt op die afstand waar door de uitdijing van het heelal punten in de ruimte met de lichtsnelheid van ons vandaan bewegen.

Contact met waarnemingen

In principe zouden de resultaten van de snaartheorie, zoals de verklaring van de microscopische entropie, en de inzichten verkregen uit de studie van  zwarte gaten toepasbaar moeten zijn in de kosmologie. Snaartheoreten zitten echter met het probleem dat deze theorie vooral goed begrepen is in anti-de Sitter-ruimte. 

Het verschil tussen anti-de Sitter-ruimte en de Sitter-ruimte is dat de eerste  een unieke grondtoestand beschrijft, terwijl de laatste moet worden voorgesteld als een aangeslagen toestand met een zeer grote entropie. Dit is precies het domein van de entropische theorie van zwaartekracht. Uit deze theorie volgt dat in aanwezigheid van een waarnemingshorizon er afwijkingen optreden van de gebruikelijke gravitatiewetten. Deze afwijkingen kunnen precies worden berekend aan de hand van de temperatuur en de entropie van de horizon. De resultaten kunnen worden vergeleken met waarnemingen. Dit biedt een spannend en hoopvol perspectief voor de entropische theorie van zwaartekracht. Feit is dat deze waarnemingen al zijn gedaan! 

Donkere materie

De wetten van Newton en de algemene relativiteitstheorie lijken overal goed te werken. Maar om dit voor elkaar te krijgen moet er op kosmologische schaal corrigerend worden opgetreden. De rotatiesnelheden in sterrenstelsels zijn bijvoorbeeld veel te groot om alle sterren en gas bij elkaar te houden enkel door de zwaartekracht van de zichtbare materie. Er moet meer zwaartekracht zijn. De ‘conservatieve’ aanname die algemeen gemaakt wordt is dat er een grote hoeveelheid donkere materie aanwezig is, in de vorm van mysterieuze deeltjes, die voor deze extra zwaartekracht zorgt. 

Uit waarneming komt echter een opvallend verband naar voren tussen de donkere materie en de zichtbare materie. Bovendien blijkt de kritische waarde van de zwaartekrachtversnelling g_krit, op de plaats waar zonder donkere materie de rotatiesnelheden beginnen af te wijken van de wet van Newton, telkens dezelfde waarde heeft. Deze kritische versnelling g_krit blijkt gelijk te zijn aan de versnelling bij de kosmologische horizon

g_krit   = cH₀.

Dit opzienbarende feit werd voor het eerst opgemerkt door Mordehai Milgrom. In 1983 vond hij [10] dat de rotatiesnelheden van melkwegstelsels konden worden beschreven via een empirische wet waarin deze versnelling een centrale rol speelt. Enkele weken na het verschijnen van mijn artikel over entropische zwaartekracht schreef Milgrom mij een brief waarin hij het vermoeden uitsprak dat mijn werk wel eens de verklaring voor donkere materie zou kunnen geven. 

In de komende lezing op Fysica 2015 op 10 april zal ik de resultaten tonen van de afwijkingen van de gebruikelijke zwaartekrachtwetten. Deze theoretische berekeningen blijken opvallend nauwkeurig overeen te komen met de kosmologische waarnemingen. Wordt ongetwijfeld vervolgd.

Referenties

1. Stephen W. Hawking, Particle creation by black holes, Commun. Math. Phys. 43, 199–220 (1975), en Black hole explosions?, Nature 248 (1974) 3031 
2. Jacob D. Bekenstein, Black holes and entropy, Phys. Rev. D 7 (1973) 2333-2346 
3. Joël Scherk en John Schwarz, Dual models for non-hadrons, Nucl. Phys. B81 (1974) 118-144
4. Michael Green, John Schwarz en Edward Witten, Superstring Theory, Vol 1 & 2, Cambridge Monographs on Mathematical Physics.
5. Gerard ’t Hooft, Dimensional reduction in quantum gravity, Salamfest 1993:0284-296 en The Scattering matrix approach to quantum black holes: an overview. Int.J.Mod.Phys. A11 (1996) 4623-4688.
6. Andrew Strominger en Cumrun Wafa, Microscopic origin of the Bekenstein-Hawking entropy, Physics Letters B, 379(1996)99, http://xxx.lanl.gov/abs/hep-th/9601029
7. Juan Martin Maldacena, The large N limit of superconformal field theories and supergravity, Adv. Theor. Math. Phys 2 (1988) 231–25, http://arxiv.org/abs/hep-th/9711200
8. Theodore A. Jacobson, Thermodynamics of spacetime: the Einstein equation of state, Physical Review Letters 75 (1995) 1260-1263
9. Erik P. Verlinde, On the origin of gravity and the laws of Newton, JHEP 04 (2011) 29, http://arxiv.org/abs/1001.0785
10. Mordehai Milgrom, A modification of the Newtonian dynamics – Implications for galaxies, Astrophysical Journal 270 (1983) 371-389