Entropie (6): Entropie en de richting van de tijd

Entropie en de richting van de tijd

Laten we, als voorbeeld van een natuurverschijnsel dat wel tijdomkeerbaar is, eens kijken naar de zwaartekracht. De zwaartekracht bepaalt hoe kanonskogels vliegen en hoe planeten om de zon draaien. Als we voor het gemak wrijving met de lucht en variaties in het zwaartekrachtveld verwaarlozen, volgen kanonskogels een baan die precies een wiskundige parabool is. (Zie afbeelding 1.) Planeten volgen banen die worden beschreven door een andere wiskundige figuur: een ellips.

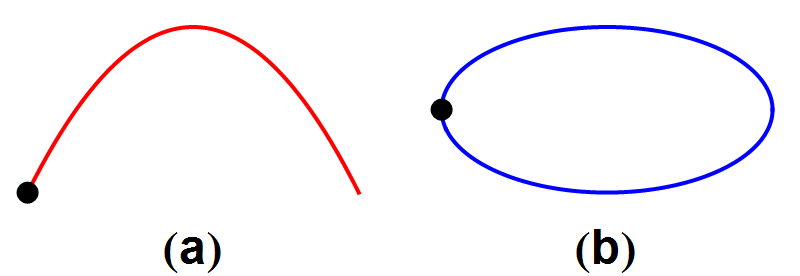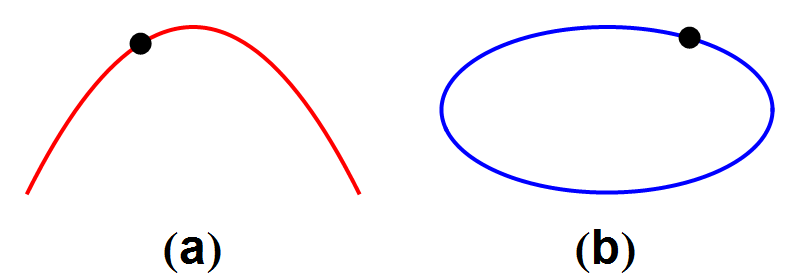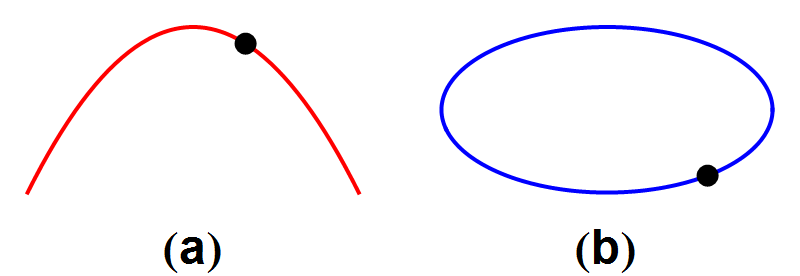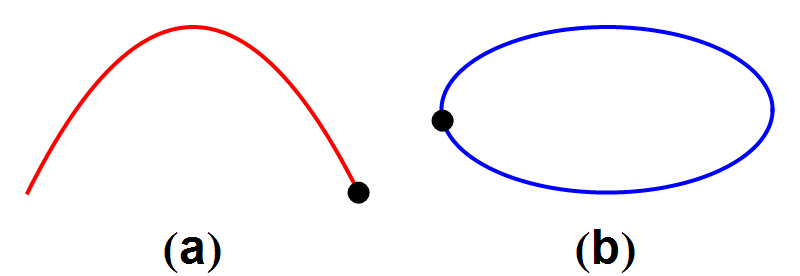
Afbeelding 1. Een kanonskogel en een komeetKanonskogels volgen banen die de vorm hebben van een parabool (a). Planeten draaien om de zon in ellipsvormige banen (b).

Beide soorten banen hebben de volgende eigenschap: wanneer we de kanonskogel of de planeet precies het omgekeerde traject laten afleggen, als in afbeelding 2, krijgen we een nieuw traject dat ook aan de zwaartekrachtswetten voldoet. Wat we zo in feite doen is het omkeren van de tijd: het is alsof we een filmpje maken van een natuurkundig proces, en dat achterstevoren afspelen. We krijgen dan een filmpje van een ander natuurkundig proces dat ook aan de natuurwetten voldoet.

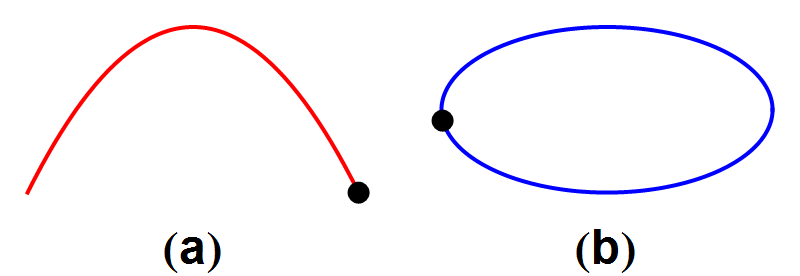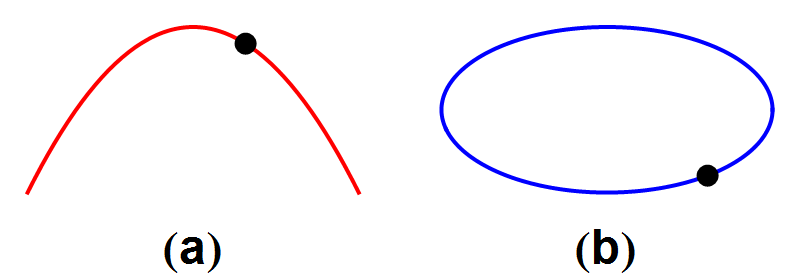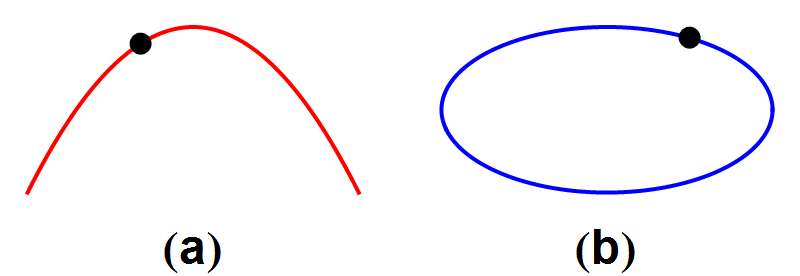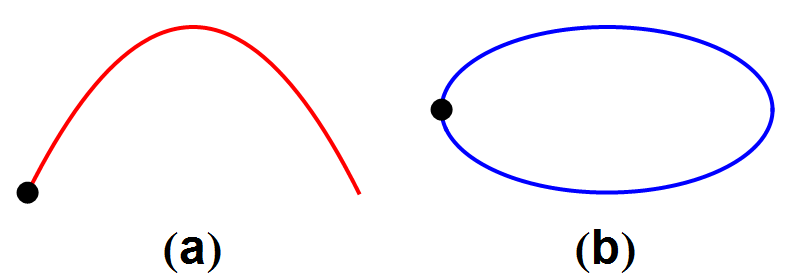
Afbeelding 2. Een kanonskogel en een komeetWanneer we de filmpjes uit afbeelding 1 achteruit afspelen, ontstaan nieuwe banen die ook aan de wetten van de natuurkunde voldoen.

Het blijkt dat deze tijdomkeerbaarheid niet alleen geldt voor de wetten van de zwaartekracht, maar ook voor vrijwel alle andere processen in de natuur die we kennen: elektrische en magnetische verschijnselen, processen binnen atomen, enzovoort. Voor sommige processen op atomaire schaal is het overigens niet genoeg om daarvoor alleen de tijdrichting om te draaien. Soms moeten we ook negatieve ladingen vervangen door even grote positieve ladingen (en omgekeerd), of moeten we het betreffende proces in spiegelbeeld uitvoeren. Hoe dan ook, er is altijd een bepaalde symmetrie die ons toestaat om de tijd om te keren, en zo een nieuw proces te vinden dat aan precies dezelfde natuurwetten voldoet.

De grote uitzondering op deze regel is de thermodynamica. Als we een filmpje maken van een leeglopende gasfles of een afkoelende kop thee, en we draaien die filmpjes achterstevoren af, zullen we zien dat de gasfles langzaam volstroomt en dat de thee langzaam uit zichzelf lijkt op te warmen. Het moge duidelijk zijn dat deze omgekeerde gebeurtenissen geen processen zijn die we in de natuur tegenkomen.

De reden dat gasflessen in de natuur nooit volstromen, hebben we inmiddels uitgebreid besproken: in dat geval zou er sprake zijn van een afname van de entropie (de eindtoestand is veel ongelijkmatiger dan de begintoestand), en de statistiek vertelt ons juist dat entropie in de loop van de tijd altijd toeneemt. De wet van de toename van entropie – de Tweede Hoofdwet – is duidelijk niet omkeerbaar in de tijd, en daarmee zijn thermodynamische processen dat dus ook niet.

Dit leidt tot de volgende, wat paradoxale situatie: we hebben gezien dat de macroscopische wetten van de thermodynamica volgen uit allerlei microscopische wetten die het gedrag van individuele atomen en dergelijke beschrijven. Als die microscopische wetten wel tijdomkeerbaar zijn, waarom is de natuurkunde waar ze op grote schaal toe leiden dat dan niet?

Het antwoord hierop ligt wederom besloten in de statistiek. Wanneer we iets preciezer over entropie nadenken, beseffen we dat het volstromen van een gasfles niet onmogelijk is, maar alleen extreem onwaarschijnlijk. Met andere woorden: we zijn ons experiment met de leegstromende gasfles begonnen vanuit een heel onwaarschijnlijke situatie, en eindigen in een veel waarschijnlijkere situatie.

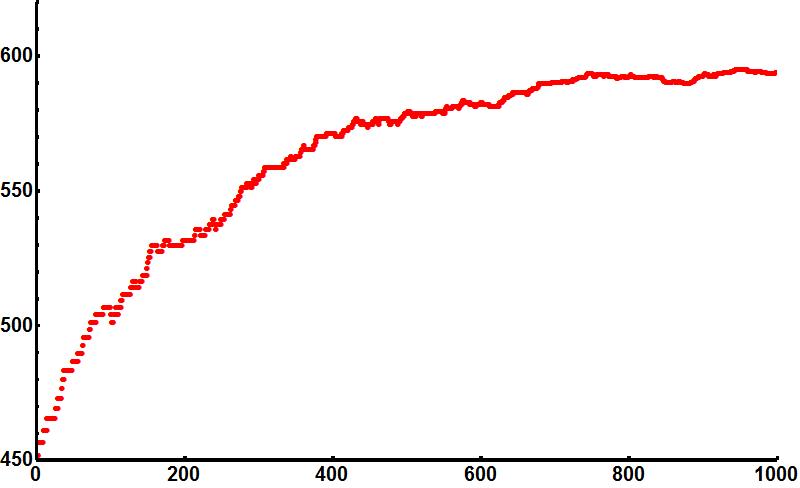
Afbeelding 3. Entropieverandering in de tijdDe entropie als functie van de tijd in een ballenbak-experiment. Horizontaal staat de tijd uitgezet (uitgedrukt in het aantal verwisselingen van een bal links met een bal rechts); vertikaal de entropie. In dit (computer-)experiment is een ballenbak gebruikt met 800 ballen, waarvan 200 rode. Aan het begin van het experiment bevinden alle rode ballen zich aan één kant; aan het eind zijn ze gelijkmatig verdeeld. We zien dat de entropie steeds toeneemt. De omgekeerde grafiek zou duiden op een extreem onwaarschijnlijk proces waarbij de ballen toevallig allemaal aan één kant eindigen.

We hadden het experiment in gedachten ook als volgt kunnen uitvoeren. We hadden kunnen beginnen vanuit een situatie waarin de gasatomen volkomen willekeurig verdeeld waren over kamer en gasfles, en een uur later het experiment kunnen stoppen. Dit is een van de meest saaie experimenten die we zouden kunnen doen, want in vrijwel alle gevallen zouden we dan beginnen in een situatie waarin de gasdruk binnen en buiten de fles gelijk is, en ook eindigen in een dergelijke situatie. Hoewel de atomen nog altijd vrij door de kamer en de fles heen vliegen, gebeurt er dus op macroscopische schaal helemaal niets: we gaan van een toestand met de hoogst mogelijke entropie naar een andere toestand met de hoogst mogelijke entropie.

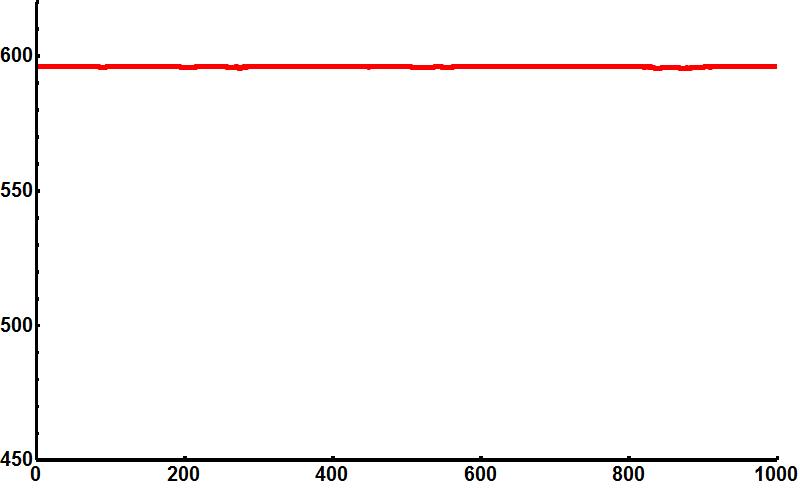
Afbeelding 4. Entropie in een evenwichtssituatieHetzelfde experiment als in afbeelding 3, maar ditmaal vanuit een begintoestand met 100 rode ballen links en 100 rechts. We zien dat de entropie vrijwel niet verandert.

Héél af en toe (en daarmee bedoelen we: eens in een aantal keren dat zo gigantisch groot is dat we de betreffende getallen niet eens kunnen opschrijven) zouden we echter puur toevallig beginnen in een situatie waarin alle atomen zich in de gasfles bevinden. En precies even af en toe zouden we puur toevallig eindigen in een situatie waarin alle atomen zich in de gasfles bevinden. In het eerste geval zal er dus een forse toename van de entropie zijn, in het tweede geval een forse afname. In dit experiment is de toename (of afname) van de entropie dus geen fundamentele natuurwet, maar iets dat heel toevallig af en toe gebeurt – en in beide richtingen even vaak.

Dat in ons daadwerkelijke experiment de entropie wel (vrijwel) altijd toeneemt komt dus niet door een tijd-asymmetrie in de natuurwetten zelf, maar door een tijd-asymmetrie in onze randvoorwaarden. We kiezen ervoor om te beginnen vanuit een statistisch gezien extreem onwaarschijnlijke situatie, en zullen daardoor vrijwel altijd eindigen in een veel waarschijnlijkere situatie.

We zouden deze redenering tot in het extreme kunnen doorvoeren: de Tweede Hoofdwet is geen gevolg van het niet-tijdomkeerbaar zijn van de microscopische natuurwetten, maar van het feit dat het heelal begonnen is in de oerknal – een situatie waarin alle materie zich op één punt bevond, en die dus extreem lage entropie had. Alle natuurkunde die in de 13,7 miljard jaar sindsdien heeft plaatsgevonden is in zeker opzicht niets anders dan het uiteffenen van die ongelijkmatigheid; één lang proces van overgangen naar steeds iets minder onwaarschijnlijke situaties.

Kortom: doordat het heelal begon in een extreem onwaarschijnlijke toestand zien we dat de entropie in de tijd altijd toeneemt, oftewel: dat de “richting van de tijd” de richting van toenemende entropie is.

Dit leidt tot de volgende vraag. Stel dat we op de één of andere manier een randvoorwaarde konden creëren waarin het heelal juist in de toekomst een heel lage entropie zou hebben in plaats van in het verleden. In de klassieke natuurkunde zouden we dit bijvoorbeeld kunnen doen door alle deeltjes waaruit het heelal is opgebouwd posities en snelheden te geven die extreem precies zijn gekozen, zodat alle atomen op een gegeven moment in gasflessen eindigen, alle scherven van een stukgevallen vaas naar elkaar toe bewegen en samen een onbeschadigde vaas vormen, enzovoort. Uiteindelijk zou het hele heelal op die manier weer samenkomen in een toestand die het tijdsomgekeerde is van de oerknal. In zo’n heelal zou de entropie langzaam maar zeker afnemen. Merk op dat de eindsituatie die we op die manier bereiken natuurlijk enorm onwaarschijnlijk is – maar dat is de beginsituatie van de echte oerknal ook!

De vraag die we nu kunnen stellen is: hoe zouden we in zo’n omgekeerd heelal de tijd ervaren? Zouden we merken dat alles langzaam maar zeker meer geordend wordt? Of zou daadwerkelijk alles omdraaien, en zouden bijvoorbeeld de beelden in onze hersenen die we als “herinneringen” ervaren nu ook een weergave van de toekomst in plaats van het verleden zijn – zodat onze “tijdservaring” effectief precies hetzelfde blijft?

Afbeelding 5. De Witte KoninginDe Witte Koningin uit Lewis Carroll’s Through the Looking Glass: “It’s a poor sort of memory that only works backwards.”

Deze laatste vraag is natuurlijk erg metafysisch van aard, en om diverse redenen moeilijk om te zetten in precieze wetenschap:

• Dit experiment is in de praktijk natuurlijk nooit uit te voeren
• Ook in theorie is het maar de vraag of een dergelijk experiment mogelijk is. In een klassiek heelal kunnen we de beginsituatie in theorie zodanig fijnafstemmen dat een extreem onwaarschijnlijke eindsituatie toch ontstaat. Of dat nog steeds mogelijk is als we de quantummechanica in onze overwegingen meenemen, is minder duidelijk.
• We weten nog te weinig van het menselijk brein om precies te kunnen zeggen hoe herinneringen en “tijdsbesef” ontstaan, en hoe deze zaken dus zouden veranderen in een hypothetisch heelal met onwaarschijnlijke randvoorwaarden aan het eind in plaats van aan het begin.

Samenvattend: het is een natuurkundig feit dat entropie toeneemt in de tijd. Dat de tijdrichting samenvalt met de richting van toenemende entropie, is een gevolg van de extreem onwaarschijnlijke randvoorwaarden aan het begin van het heelal. We kunnen ons afvragen of we deze observatie zouden moeten omdraaien, en of we dus de richting van de tijd zouden moeten definiëren als de richting waarin de entropie toeneemt. Als onze hersenen in een “omgekeerd heelal” zoals hierboven inderdaad de tijd omgekeerd zouden ervaren, zou zo’n definitie zinvol zijn. Of dat het geval is, is helaas een vraag waarop het antwoord nog ver buiten het bereik van de moderne wetenschap ligt.

Dit is het zesde artikel uit het dossier Entropie. In het zevende artikel zien we aan de hand van het voorbeeld van een samentrekkende gaswolk dat entropie altijd toeneemt – ook in situaties waar dat in eerste instantie niet zo lijkt te zijn.