
Afbeelding 1. Robert Langlands.Foto: Jeff Mozzochi / Robert Langlands.
Wat noemen we binnen de wetenschap een “grootse ontdekking”? Sommige ideeën, zoals de relativiteitstheorie, zijn zo vernieuwend en baanbrekend dat ze een op zichzelf staand onderzoeksgebied creëren. Ook vandaag de dag, meer dan honderd jaar nadat Einstein zijn vergelijkingen opschreef, wordt er nog regelmatig gedebatteerd over fundamentele eigenschappen van zijn theorie. Met zijn beschrijving van de zwaartekracht is Einstein in zekere zin een heel nieuw pad ingeslagen, en we hebben nog steeds niet helemaal in kaart gebracht waar dat pad naartoe leidt.
Dit is echter niet het soort ontdekking waarvoor Robert Langlands vorige maand de Abelprijs kreeg. Niet elke grootse ontdekking hoeft nieuw land droog te leggen. Soms blijkt juist dat de taal die we tot nu toe gebruikt hebben om bepaalde problemen te formuleren niet de goede is, net alsof je in het Chinees de weg probeert te vragen op de Noordpool. Héél af en toe ontdekt men een woordenboek waarmee we zulke problemen kunnen vertalen. In sommige gevallen, zoals in de AdS/CFT-correspondentie, blijken moeilijke problemen in de ene taal eenvoudig te worden zodra ze in de andere taal vertaald zijn. En zelfs als dat niet het geval is, geeft alleen het bestaan van het woordenboek al een nieuw en onverwacht perspectief. Door een nieuwe kijk op bestaande problemen te benutten, kunnen wetenschappers nieuwe strategieën bedenken om die problemen aan te pakken.
Langlands heeft zijn prijs gewonnen vanwege een vermoeden wat hij ooit schoorvoetend in een zeventien kantjes tellende brief voorlegde aan een van de grootste wiskundigen van dat moment, André Weil. In deze brief opperde Langlands een verband tussen twee op het eerste gezicht ongerelateerde problemen. De precieze wiskundige formulering van zijn vermoeden is lastig te begrijpen, maar kort door de bocht gezegd ontdekte Langlands dat er verbanden lijken te bestaan tussen de symmetrieën van op het eerste gezicht totaal ongerelateerde problemen. Zulke symmetrieën worden wiskundig beschreven door structuren die we groepen noemen, en de groepen die in het idee van Langlands aan elkaar gerelateerd worden, noemt men ook wel Langlands-duaal.
Tot verbazing van velen bleek dat een zekere vorm van deze puur wiskundig gemotiveerde vermoedens te begrijpen was vanuit de natuurkunde. Deze ontdekking, die heel levendig beschreven wordt in het boek “Love and Math” van de Amerikaans-Russische wiskundige Ed Frenkel, kunnen we in hun simpelste vorm begrijpen aan de hand van het elektromagnetisme.
Aan het eind van de 19e eeuw ontdekte de Britse natuurkundige J.J. Thomson dat elektriciteit door fundamentele deeltjes wordt overgebracht – deeltjes die tegenwoordig bekend staan als elektronen. Deze bouwstenen van de elektriciteit hebben altijd exact dezelfde massa en exact dezelfde elektrische lading. De precieze grootte van die lading werd aan het begin van de 20e eeuw in Amerika door Robert Millikan gemeten. Elektrisch geladen deeltjes oefenen dankzij die lading een kracht op elkaar uit die beschreven kan worden met behulp van een veld dat zich tussen de deeltjes bevindt.
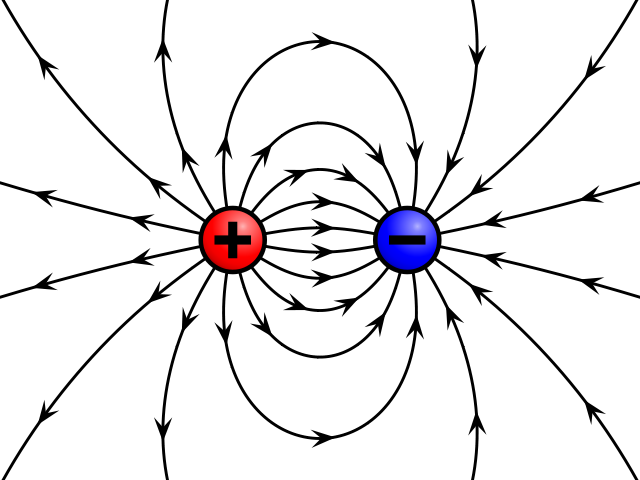
Afbeelding 2. Een elektrisch veld.Elektrische veldlijnen tussen een positieve en negatieve lading. Afbeelding: Wikipedia-gebruiker Geek3.
In veel van onze elektrische apparaten speelt magnetisme ook een belangrijke rol. De dynamo op je fiets wekt bijvoorbeeld elektriciteit op door een spoel om een magneet te bewegen, waardoor er een stroom door de spoel gaat lopen die uiteindelijk je licht laat branden. Magneten zoals die in je dynamo bestaan echter altijd uit twee polen waartussen de magnetische veldlijnen lopen.
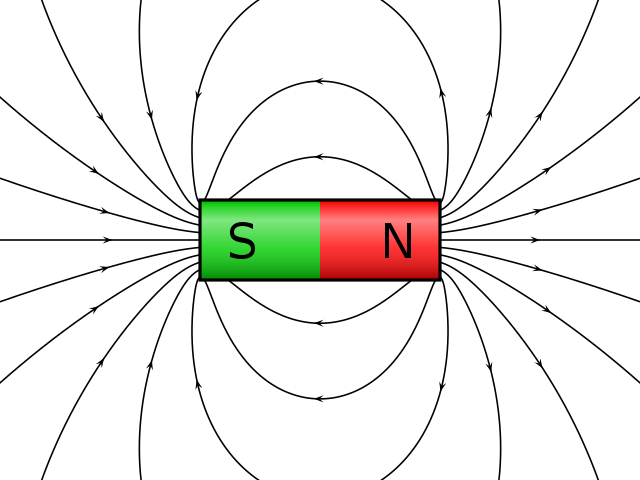
Afbeelding 3. Een magnetisch veld.Magnetische veldlijnen gaan altijd van een noord- naar een zuidpool. Afbeelding: Wikipedia-gebruiker Geek3.
Niemand heeft ooit een enkel magnetisch geladen deeltje, een zogenaamde magnetische monopool, gezien. Natuurkundig gezien is dat in principe geen probleem: zijn ze er niet, dan zijn ze er niet. Het is echter vrij makkelijk om de wiskundige vergelijkingen die elektriciteit en magnetisme beschrijven, zó aan te passen dat zulke magnetische monopolen wel kunnen bestaan.
Deze interessante truc werd voor het eerst uitgehaald door de Britse natuurkundige Paul Dirac, aan het begin van de 20e eeuw. Hij ontdekte dat áls er een magnetische monopool bestaat, het elektrisch veld zich daar als het ware omheen moet winden. Dit kan je je voorstellen als het winden van je hangslot om je zadel. Je wikkelt het slot er een bepaald aantal keer omheen en doet het dan dicht. Vanaf dat moment kan je het aantal windingen niet meer veranderen. Het aantal windingen wordt het windingsgetal genoemd. Dirac ontdekte dat dit windingsgetal overeenkomt met de hoeveelheid elektrische lading die “om de magnetische monopool gewikkeld is”. Een winding toevoegen zou dus neerkomen op het toevoegen van een precies bepaalde eenheid aan elektrische lading. Hiermee vond Dirac dus een theoretische verklaring voor het bestaan van een kleinste bouwsteen van elektrische lading!

Afbeelding 4. Een fietsslot met windingsgetal 4.Het windingsgetal kan alleen in hele eenheden toe- of afnemen.
Als er zowel elektrisch als magnetisch geladen deeltjes bestaan, blijkt er ook nog een grotere truc mogelijk te zijn. Je kan de elektrische en magnetische bouwstenen omwisselen, als je ook tegelijkertijd alle elektrische velden in magnetische velden verandert en vice versa. Het resultaat is dan nog altijd een fysisch mogelijke configuratie. Het verrassende is echter dat de vergelijkingen dit omwisselen alleen maar toestaan als de nieuwe magnetische lading de inverse is van de oude elektrische lading: één gedeeld door die lading, dus. Aangezien de lading van een elektron heel klein is, betekent dit dat de magnetische lading van de corresponderende magnetische monopool enorm groot moet zijn.
Deze “dualiteit” in het elektromagnetisme werd lang als een rariteit gezien. Het is immers veel makkelijker om met kleine en daadwerkelijk bestaande elektrische ladingen te rekenen dan met hypothetische en bovendien enorme magnetische monopolen. In de jaren zeventig ontdekten Claus Montonen en David Olive echter dat het mogelijk is om de elektromagnetische dualiteit uit te bereiden naar verfijndere theorieën die veel meer deeltjes beschrijven. Net als in het standaardmodel van de elementaire deeltjes, waarin alle deeltjes zijn beschreven waaruit het universum bestaat, worden deze deeltjes gelabeld door een symmetriegroep. Symmetriegroepen beschrijven wat je allemaal kunt doen met een object, zonder dat het verandert. Een vierkant kun je bijvoorbeeld spiegelen door verschillende assen, maar ook over bepaalde hoeken draaien, zonder dat het vierkant er anders uit komt te zien. De precieze informatie over hoe je kunt spiegelen en draaien, is beschreven in de symmetriegroep. Wiskundig gezien kun je deeltjes, net als een vierkant, ook ‘spiegelen’ en ‘draaien’, maar niet alle deeltjes op dezelfde manier – net zoals een vierkant en een vijfhoek niet dezelfde symmetrieën en dus niet dezelfde symmetriegroep hebben. Verschillende deeltjes hebben dus verschillende symmetriegroepen.
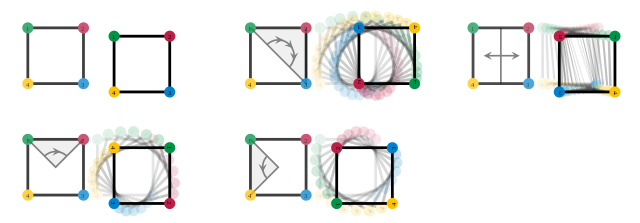
Afbeelding 5. Symmetrieën van een vierkant.Links zien we steeds het oorspronkelijke vierkant met een pijltje dat de symmetrie (rotatie, spiegeling, of “helemaal niets doen”) aangeeft; rechts het resultaat als de symmetrie is toegepast. Afbeelding: Timothy Rias en Jack Schmidt.
De Montonen-Olivedualiteit, ook wel bekend als S-dualiteit, wisselt wederom licht elektrisch geladen deeltjes om met sterk magnetisch geladen deeltjes. Daarmee blijkt echter ook de symmetriegroep te veranderen, en tot ieders verbazing wordt dit precies de duale groep die Langlands voorspelde!
De bovenstaande ontdekking is al gedaan in de jaren zeventig, maar lange tijd was de vorm waarin de duale groep van Langlands opdook in de Montonen-Olivedualiteit een groot mysterie. Aan het begin van de 21e eeuw werd echter langzaam duidelijk hoe dit verklaard kan worden. In een enorm boekwerk legden Edward Witten en Anton Kapustin uit dat de precieze vorm waarin de dualiteit naar voren komt, pas echt begrepen kan worden als we niet meer alleen naar deeltjes kijken, maar naar branen. Wat branen precies zijn, is beschreven in dit eerdere artikel, maar voor nu is alleen van belang dat het gaat om objecten die elektrisch of magnetisch geladen kunnen zijn. Als we deze branen weer omwisselen, net als de elektrisch en magnetisch geladen deeltjes, komen de voorspelde verbanden van Langlands in nog algemenere vorm naar boven.
Het moge duidelijk zijn dat het laatste woord over deze bijzondere observaties nog niet gezegd is. De elektromagnetische interpretatie van de wiskundige vermoedens van Langlands heeft slechts een tipje van de sluier opgelicht, want die fysische situatie beschrijft nog niet eens de volledige versie van zijn vermoedens. Misschien kunnen er met behulp van de rest van Langlands’ vermoedens nog wel andere dualiteiten in de natuurkunde worden gevonden, die ons een vernieuwende blik geven op bestaande theorieën. Hoe dan ook was zijn ontdekking van enorm grote waarde, in de natuurkunde en natuurlijk in de wiskunde zelf. Ruim vijftig jaar nadat hij zijn beroemde brief naar Weil stuurde, verdient Robert Langlands het daarom zonder meer om even in de spotlights te staan.