Heel veel deeltjes samen: thermodynamica
Op dit moment heeft de natuurkunde een heel scala aan theorieën beschikbaar om het gedrag van de natuur om ons heen te voorspellen. Voor voorwerpen in ons dagelijks leven gebruiken we klassieke mechanica om hun gedrag te beschrijven. Voor heel snel bewegende of heel zware voorwerpen hebben we Einsteins relativiteitstheorie, en voor heel kleine objecten hebben we de quantummechanica. Een belangrijke eis die we stellen aan onze theorieën van de natuur, is dat ze in de randgevallen in elkaar overlopen. Relativiteitstheorie benadert de normale klassieke mechanica voor lage snelheden en kleine massa’s, en de verwachtingswaardes die we krijgen uit de Schrödingervergelijking komen netjes overeen met de klassieke berekeningen.
Naast deze voorbeelden van theorieën in de natuurkunde bestaat er nog een andere belangrijke tak van de natuurkunde: thermodynamica. Zoals eerder beschreven op deze website zijn de klassieke mechanica en de thermodynamica prima verenigbaar met elkaar. Daar ligt vooralsnog geen probleem. Wat wij ons voor dit artikel afvragen, is of de quantummechanica wel te verenigen is met thermodynamica. Er lijken hier namelijk een paar kleine problemen te ontstaan.
Thermodynamica betreft de empirisch vastgestelde wetten die het gedrag van (bijvoorbeeld) gassen voorspellen. Zulke gassen bestaan uit atomen die rondvliegen in een bepaalde ruimte, bijvoorbeeld in een cilinder in een automotor. De voorspellingen die de thermodynamica doet zijn uitvoerig getest in laboratoria, en blijken bijzonder accuraat. Aan de andere kant voorspelt de quantummechanica óók het gedrag van deze deeltjes in een gas. We zouden dus verwachten dat beide theorieën hetzelfde voorspellen in bepaalde limietgevallen. We weten immers dat ook quantummechanica een geweldig goed werkende theorie is, wellicht de meest uitgebreid geteste theorie van allemaal.

Afbeelding 1. Een stirlingmotor.Een stirlingmotor werkt op basis van uitzettende gassen in cilinders, en is daarmee een typisch voorbeeld van een toepassing van de thermodynamica. Links: een voorbeeld van een draaiende stirlingmotor. Rechts: een volume-drukdiagram voor een stirlingmotor, berekend met behulp van de wetten van de thermodynamica. Aan de hand van dit diagram is het mogelijk om precies te voorspellen wat er gebeurt met het gas in de motor. Afbeelding links: Paul U. Ehmer. Afbeelding rechts: AkanoToE.
Van quantummechanica naar thermodynamica?
Laten we nu aan de hand van een voorbeeld eens bekijken of deze twee theorieën, quantummechanica en thermodynamica, verenigbaar zijn. We kijken daarvoor naar een systeem dat we kunnen beschrijven met thermodynamica: een gas. Als we een gas in een oven doen, dan zal in de loop van de tijd het gas opwarmen, totdat het dezelfde temperatuur heeft als de verwarmingselementen in de oven. We zeggen nu dat het gas in evenwicht is met de omgeving. Het proces dat het gas ondergaat om in evenwicht te komen heet thermalizeren. Nu is het mogelijk om, met behulp van de thermodynamica, deze toestand te beschrijven met slechts een paar getallen: de temperatuur van het gas, de temperatuur van de oven en bijvoorbeeld nog een getal dat ons vertelt hoe goed het gas warmte geleidt. Wellicht zijn er nog wat andere grootheden nodig, maar het idee is duidelijk: met enkele getallen kunnen we de toestand van ons gas beschrijven.
Aan de andere kant hebben we de quantummechanica. De Schrödingervergelijking vertelt ons dat de functie die de toestand van ons gas beschrijft, volledig afhangt van de oorspronkelijke toestand van het gas: elk atoom in het gas bevat informatie over de begintoestand. Een macroscopische hoeveelheid gas zal in de orde van 1 mol (een getal van 23 cijfers) aan atomen hebben, die onderling interacties hebben met elkaar. Om ook de interacties die voorkomen in een gas tussen de atomen onderling te beschrijven, blijken we nog eens de e-macht van het aantal atomen te moeten nemen. Zo krijgen we een getal dat zelf grofweg een mol aan cijfers heeft! Hoe kan dat? Aan de thermodynamicakant hebben we maar een beetje informatie nodig, en aan de quantumkant meer informatie dan je je kunt voorstellen. Het lijkt erop dat heel veel informatie van de initiële quantumtoestand verloren gaat gedurende het in evenwicht komen van ons thermodynamische systeem – het is dit proces van steeds minder informatie nodig hebben dat ‘thermalizeren’ wordt genoemd.
We kunnen nu dus stellen dat het proces van thermalizeren een quantumtoestand op de een of andere manier reduceert naar een toestand die we kunnen beschrijven met behulp van de wetten van thermodynamica, ‘een thermodynamische toestand’. Nu moeten we maar liefst vier vragen beantwoorden:
- Wat bedoelen we met een ‘thermodynamische toestand’?
- Wat betekent ‘thermalizeren’ precies?
- Hoe thermaliseert een klassieke toestand?
- Hoe thermaliseert een quantumtoestand?
Met name de laatste vraag blijkt lastig te beantwoorden, en dat is precies wat een idee dat recent veel aanhang heeft gevonden in de theoretische natuurkunde, de Eigenstate Thermalisation Hypothesis tracht te bereiken. Als deze hypothese klopt, dan weten we hoe een quantummechanische toestand in de thermodynamische limiet (wanneer een enkel systeem heel veel deeltjes bevat) reduceert naar een toestand die hetzelfde is als de thermodynamische toestand, en kunnen we weer rustig ademhalen. Alles werkt naar behoren.
Wat bedoelen we met een ‘thermodynamische toestand’?
Een thermodynamische toestand is een toestand waarin een systeem van deeltjes zich in een thermodynamisch evenwicht bevindt. We kunnen deze toestand beschrijven met behulp van de wetten van de thermodynamica. Om concreet te zijn moeten we nog wel precies maken wanneer we een systeem kunnen beschrijven met behulp van thermodynamische identiteiten. Hiervoor moeten we even kort teruggrijpen op onze kennis van de klassieke mechanica van Isaac Newton. In de klassieke mechanica kunnen we een systeem (bijvoorbeeld een gas gemaakt van harde balletjes die rondvliegen in de ruimte) volledig beschrijven als we de volgende twee eigenschappen van alle objecten in het systeem weten: waar is het, en waar gaat het heen? Met andere woorden: we moeten weten wat de plaats van een deeltje is en de snelheid (of iets preciezer: de impuls) van dat deeltje op die plaats. Deze coördinaten geven ons een punt in wat we de faseruimte van ons systeem noemen.
Elk punt in deze faseruimte komt overeen met wat we een ‘microscopische toestand’ noemen. Zo is er een punt in de faseruimte van een gas in een afgesloten container die overeenkomt met de microscopische toestand waarin alle deeltjes van het systeem exact egaal verdeeld zijn over alle beschikbare ruimte, en alle energie en impuls onderling precies eerlijk hebben verdeeld. Nu maken we een belangrijke aanname over het systeem dat we willen beschrijven. We stellen dat de kans dat we een toestand vinden die ligt in een bepaald stukje van onze faseruimte, evenredig is met het volume van dat stuk faseruimte. Kort gezegd: de grootte bepaalt de kans. Een systeem dat hieraan voldoet, noemen we ergodisch. Simpel gezegd betekend ergodiciteit, dat elke microscopische toestand even waarschijnlijk is. Dit is een zeer belangrijke aanname, en staat ten grondslag aan de wetten van thermodynamica. Opvallend genoeg is het vaak heel lastig om ook echt te bewijzen dat een systeem ergodisch is, maar uit metingen blijkt dat vrijwel alle grote systemen (grofweg: dingen die je met je handen kan vastpakken in het dagelijks leven) ergodisch zijn.
Een eigenschap gerelateerd is aan ergodiciteit, is chaos. In een vorig artikel op deze website wordt chaos geïntroduceerd. Kort gezegd is een systeem chaotisch als door een zeer kleine aanpassing aan de begincondities, het systeem uiteindelijk in een totaal andere toestand zal eindigen.Voor ons is het voldoende om te weten dat als een systeem chaotisch is, het ook ergodisch zal zijn in het klassieke regime waarbij we heel veel atomen tegelijk bekijken. Concluderend hebben we dus de volgende implicaties: een chaotisch systeem impliceert een ergodisch systeem, wat uiteindelijk thermodynamica impliceert:
Chaotisch → Ergodisch → Thermodynamica
De aanname van ergodiciteit betekent dus dat elke configuratie in ons systeem een gelijke kans heeft. Dit betekent weer dat we in principe de kansverdeling weten van onze microscopische toestanden. Deze kansverdeling heet ook wel het ‘microkanonieke ensemble’.
Wat betekent ‘thermalizeren’ precies?
Als we een systeem willen beschrijven, zeggen we vaak een paar dingen – bijvoorbeeld: het systeem heeft x deeltjes, een temperatuur van y graden Celsius, en dimensies van lengte a × breedte b × hoogte c. Wat we aan elkaar vertellen zijn ‘observabelen’: eigenschappen van het systeem die je kan meten.
Een systeem thermaliseert, als gedurende de tijdsevolutie van het systeem de observabele de waarde krijgt die voorspeld wordt door het microkanonieke ensemble. In simpele woorden: als we een systeem een tijdje laten begaan, dan is het gethermaliseerd wanneer de meetwaardes van dat systeem overeenkomen met de waardes die we voorspellen uit de thermodynamica.
Hoe thermaliseert een klassieke toestand?
Klassiek gezien kan je je eenvoudig voorstellen hoe een klassiek systeem thermaliseert. Neem ter illustratie een gas bestaande uit klassieke deeltjes, dat zich oorspronkelijk in een bepaalde microscopische toestand bevindt, bijvoorbeeld een heel speciale toestand waarin alle beschikbare energie gestopt is in de beweging van één enkel deeltje in het gas. Dit deeltje zal dan door de ruimte vliegen, en botsen met andere deeltjes. Bij deze botsingen raakt het deeltje energie en impuls kwijt, en zo worden die grootheden langzaamaan verdeeld over alle deeltjes in het gas. Dit proces gaat de hele tijd door. Op deze manier beweegt ons systeem zich door de faseruimte Als we nu een tijdje wachten, zal ons systeem naar verwachting naar een toestand gaan, waarin de kansverdeling overeenkomt met die van het microkanonieke ensemble.
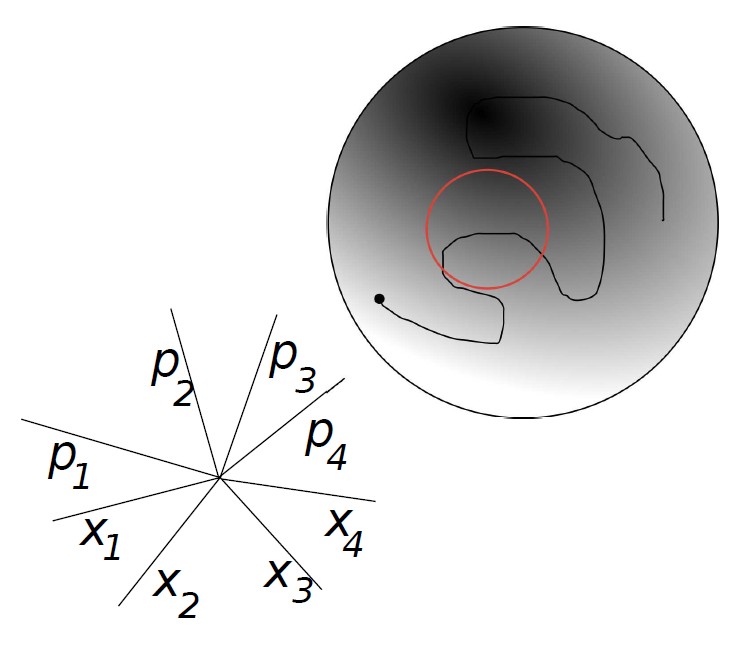
Afbeelding 2. Een voorbeeld van een faseruimte.De cirkel stelt een multidimensionale ruimte voor waarvan de coördinaten worden gegeven door vier plaats- en vier impulsrichtingen. (Acht coördinaatassen loodrecht op elkaar tekenen lukt natuurlijk niet op tweedimensionaal papier, maar het idee is linksonder geschetst.) De zwarte lijn laat zien hoe een systeem in de loop van de tijd door de faseruimte heen beweegt. De rode lijn is een voorbeeld van een systeem dat periodiek terugkomt bij zijn oorspronkelijke toestand. Dit is dus een voorbeeld van een systeem dat nooit zal thermaliseren! Afbeelding uit J. M. Deutsch, Eigenstate Thermalization Hypothesis.
Hoe thermaliseert een quantumtoestand?
Om de het thermaliseren van een quantumtoestand te beschrijven zou je kunnen denken dat we hetzelfde recept kunnen volgen. Helaas is er in elk geval één belangrijk verschil tussen klassieke en quantummechanica: in de quantummechanica kunnen we geen faseruimte beschrijven zoals in het klassieke geval. Volgens Heisenbergs onzekerheidsprincipe kunnen we niet tegelijkertijd exact weten waar we zijn én hoe hard we gaan. We moeten kiezen welke van die eigenschappen we willen weten, en moeten dan accepteren dat de ander niet eenduidig bepaald is. Los van dit probleem zijn er nog enkele andere verschillen tussen de quantummechanische beschrijving en de klassieke beschrijving van hierboven. Het antwoord op de vraag ‘Hoe thermaliseert een quantumtoestand?’ kunnen we gelukkig alsnog geven: dat gebeurt door interacties tussen de atomen onderling. De vraag is alleen waar dit ons naartoe brengt. Bij de klassieke beschrijving van hierboven ging ons systeem door een faseruimte bewegen waaruit de rest volgde; nu is het veel lastiger om precies aan te geven wat er gebeurt.
Gelukkig is het formalisme van de quantummechanica wel krachtig genoeg om ons een exacte formule te geven voor het tijds-gemiddelde van een observabele. Deze formule hangt van alle begincondities af en zegt op zichzelf nog niets over een mogelijkheid van thermaliseren. Het blijkt echter dat we, in de thermodynamische limiet van heel veel atomen, wel een paar observaties kunnen doen die hoop lijken te geven. Als we namelijk een systeem hebben met veel atomen, dan kunnen we zeggen dat we een complex systeem hebben. Normaal gesproken kunnen we zo’n complex systeem überhaupt heel moeilijk exact beschrijven, en daarom bedachten natuurkundigen in de 20e eeuw dat het wellicht slim is om dit ook niet te proberen, maar een extra aanname te maken: een complex systeem wordt beschreven met behulp van een ‘toevalsmatrix’. Hoe deze objecten precies werken is onlangs ook al beschreven op deze website. Voor ons verhaal is het voldoende om te weten hoe de statistiek van de verwachtingswaardes van operatoren van golffuncties die volgen uit een toevalsmatrix zich gedraagt. Dat is een hele mond vol, maar het wil zeggen: we willen weten wat de kansrekening voor dit geval is. En laat deze kansrekening nou precies die van het microkanonieke ensemble zijn!
Dit besef bracht de natuurkundegemeenschap uiteindelijk tot de Eigenstate Thermalization Hypothesis. De hypothese is kort samengevat als volgt: de verwachtingswaarde van een observabele van een complex systeem is gegeven door de gemiddelde waarde in de loop van de tijd plus kleine afwijkingen. Als de verwachte meetwaarde inderdaad de tijds-gemiddelde waarde is, dan is dat ook precies wat we krijgen als resultaat van het microkanonieke ensemble van de thermodynamica. Dit lijkt bijna een té makkelijke oplossing – het gemiddelde over de hele fase-ruimte hoeft alleen maar hetzelfde te zijn als het gemiddelde van een specifieke toestand in de loop van de tijd – maar dat is het zeker niet! Dat de verwachtingswaardes van een bepaald complex systeem zich op een dergelijke manier gedragen is helemaal niet vanzelfsprekend. Veel van de systemen die we kennen in de quantummechanica hebben juist een heel specifiek spectrum van verwachtingswaardes, die ook nog eens flink kunnen oscilleren in de tijd. Als deze oscillaties van de verwachtingswaarde heel heftig zouden zijn, dan zou ons systeem nooit naar een bepaald gemiddelde convergeren, en dus ook niet ‘thermaliseren’. Het lijkt er echter op dat, als een systeem erg complex wordt, bijvoorbeeld in het thermodynamisch limiet, met veel deeltjes, die allemaal interacties met elkaar aangaan, de verwachtingswaardes van een dergelijk quantummechanisch systeem zich precies gedragen zoals we zouden willen.
Kortom: als de Eigenstate Thermalization Hypothesis waar is, weten we zeker dat we thermodynamica niet alleen op de klassieke mechanica maar ook op de quantummechanica mogen toepassen. De volgende vraag is natuurlijk: hoe bewijs je zoiets? Dat is een vraag waar natuurkundigen zich nog steeds het hoofd over breken, en waarop het antwoord nog niet bekend is. Wordt dus ongetwijfeld vervolgd!
Voor wie zelf graag in de wetenschappelijke literatuur over dit onderwerp wil duiken: voor het schrijven van dit artikel is gebruikgemaakt van ‘Eigenstate Thermalization Hypothesis’ van Joshua. M. Deutsch en van ‘From Quantum Chaos and Eigenstate Thermalization to Statistical Mechanics and Thermodynamics’ van Luca D’Alessio, Yariv Kafri, Anatoli Polkovnikov en Marcos Rigol.