
Kristallen
Om te begrijpen waarom quasikristallen bijzonder zijn, moeten we eerst iets weten over normale kristallen. Kristallen zijn materialen die bestaan uit hetzelfde stukje dat steeds opnieuw wordt herhaald. Deze stukjes noemen we eenheidscellen. In elke eenheidscel in een materiaal zitten een of meerdere atomen in steeds hetzelfde patroon. We zullen het hier vooral hebben over kristallen in twee dimensies, omdat die het makkelijkst te tekenen en in te beelden zijn, maar zowel driedimensionale als eendimensionale kristallen zullen later ook terugkomen. Het ‘opbouwen’ van een tweedimensionaal kristal werkt hetzelfde als het betegelen van een muur. Je kan je badkamermuur betegelen met allemaal vierkante tegeltjes door naast en boven elk tegeltje een nieuw tegeltje te plaatsen. Alle vierkante tegeltjes zijn gelijk van vorm, en door ze mooi aansluitend neer te leggen krijg je een betegelde muur. Een vierkant rooster in een kristal is precies hetzelfde, alleen is elk tegeltje een eenheidscel met daarin een atoom.
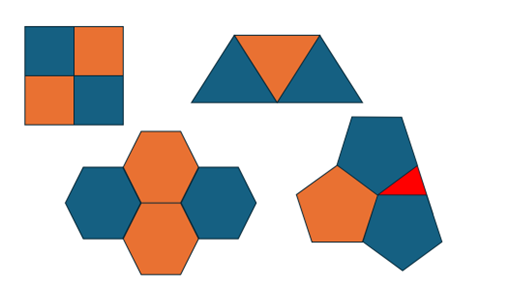
Om een kristal te kunnen maken moet een steeds herhaalde eenheidscel de hele ruimte kunnen vullen zonder dat er gaten vallen of cellen overlappen. Dit kan alleen als de eenheidscellen een bepaalde rotatiesymmetrie hebben. Iets heeft een rotatiesymmetrie als het na een aantal graden gedraaid te worden weer precies hetzelfde is als voorheen. Hierbij is het belangrijk onderscheid te maken tussen de symmetrie van de eenheidscel zelf en de symmetrie van de structuren of patronen binnen de eenheidscel: de eerste bepaalt of het hele vlak of volume probleemloos kan worden gevuld, terwijl de tweede invloed heeft op de interne eigenschappen van het kristal. Je kan je bijvoorbeeld een badkamertegel voorstellen met een uitstekend stukje aan de ene kant en een inkeping aan de andere, zodat ze steeds perfect in elkaar passen. Je kan dan nog steeds atomen op het midden van de tegeltjes plaatsen. Dit levert het zelfde vierkante rooster op met viervoudige rotatiesymmetrie, terwijl de tegels niet meer viervoudig rotatiesymmetrisch zijn.
Je kan je voorstellen dat je je badkamer ook kan betegelen met rechthoekige, driehoekige of zeshoekige tegeltjes, elk met hun eigen rotatiesymmetrie, maar het betegelen van je muur met een regelmatige vijfhoek lukt niet: dan vallen er gaten. Het feit dat je geen heel vlak kan bedekken met vormen met vijfvoudige (en zevenvoudige en achtvoudige, etc.) rotatiesymmetrie zonder dat er gaten vallen, leidde tot de voorspelling dat kristallen alleen zouden kunnen bestaan uit einheidscellen met twee-, drie-, vier- en zesvoudige rotatiesymmetrie.
Kijken in een kristal
Uit een dergelijke voorspelling volgt natuurlijk de vraag hoe je zulke symmetrieën op zulke extreem kleine schaal zou kunnen meten. Er werd hiervoor meer dan een eeuw geleden al gekeken naar de uitwendige vorm van het kristal. Hoewel die soms een indicatie kan geven voor de vorm van de eenheidscel, is die vorm er vaak niet aan af te lezen. Door gebruik te maken van röntgenstraling of elektronen met lage energie kan je ín het kristal kijken. Nu denk je misschien aan een röntgenfoto, maar we hebben het hier over een heel ander proces. Een kristal heeft door zijn regelmatige ordening doorsnedes met een hoge dichtheid aan atomen en vlakken waar helemaal geen atomen zitten. Hierdoor werkt elk kristal als een soort natuurlijke (transmissie-) tralie. Zo’n tralie bestaat uit spleten die meer licht doorlaten in een materiaal dat minder licht doorlaat. Als licht, of een andere golf, door meerdere spleten naast elkaar wordt gestuurd, dan tellen de verschillende delen van de golf die door de verschillende spleten gaan zo bij elkaar op dat er een patroon ontstaat met delen met veel licht en met weinig tot geen licht. Dit gebeurt met name als de golflengte van de golf ongeveer overeenkomt met de afstand tussen de spleten.

De vlakken van hogere en lagere dichtheid in een kristal geven een complex patroon van spleten in meerdere richtingen. Dit levert ook een complex diffractiepatroon bestaande uit veel punten als er licht of elektronen van vergelijkbare golflengte op worden ingezonden. Deze punten geven de symmetrie van het kristal weer, omdat de informatie daarover in feite zit in de plaatsing van de vlakken van atomen met hogere dichtheid. Met name rotatiesymmetrie is meteen zichtbaar omdat het diffractiepatroon dezelfde rotatiesymmetrie heeft als het kristal. Dit is bijvoorbeeld heel mooi te zien in het diffractiepatroon van kopersulfaat, een kristal met viervoudige rotatiesymmetrie.

Ontdekking van het quasikristal
Nu we scherp hebben wat kristallen zijn en hoe we ze onderzoeken komen we aan bij de beloofde quasikristallen. Scheikundige Daniel Schechtman was in 1982 tijdens een ‘sabbatical year’ aangesteld bij het huidige National Institute for Standards and Technology als elektronenmicroscoopexpert. Daar deed hij onderzoek naar snel afgekoelde metalen en legeringen. Toen hij een legering van aluminium en mangaan met een elektronenmicroscoop bestudeerde, zag hij een vijfvoudige symmetrie. Dit was opvallend omdat men zoals gezegd dacht dat alleen kristallen met twee-, drie-, vier- en zesvoudige symmetrie konden bestaan. Daarom besloot Schechtman om het materiaal te bestuderen met elektronendiffractie en daaruit kwam een schitterend diffractiepatroon mét vijfvoudige symmetrie. Het duurde echter nog twee jaar voor er iets met dit resultaat gedaan werd, want alle ervaren kristallografen aan wie hij het resultaat liet zien, zeiden simpelweg dat kristallen met vijfvoudige symmetrie niet kunnen bestaan en dat hij dus fout gemeten moest hebben. Dat vijfvoudige symmetrie onwaarschijnlijk was wist Shechtman ook wel, maar het lukte ook niet om een andere verklaring te vinden en hij mat steeds hetzelfde, hoe vaak hij het ook opnieuw deed.

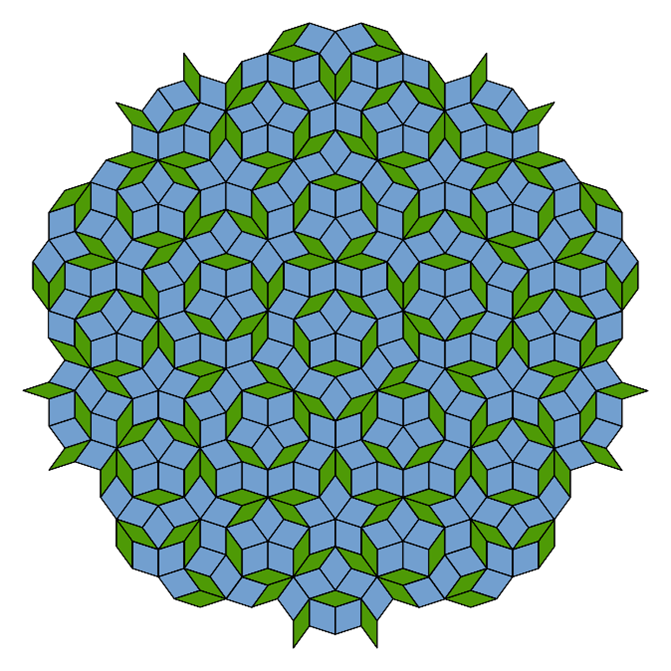
Wat Shechtman niet wist, was dat wiskundige Alan Mackay in 1981 een voorspelling had gedaan die cruciaal bleek voor het verklaren van zijn resultaten. Mackays voorspelling ging over de zogenaamde “Penrose-betegeling,” een patroon met een vijfvoudige rotatiesymmetrie. Deze betegeling maakt gebruik van twee verschillende ruitvormige tegels. Roger Penrose toonde aan dat je met deze tegels een vlak volledig kunt bedekken zonder dat het patroon zich herhaalt. Toch vertoont het patroon een bepaalde mate van ordening: het bestaat volledig uit dezelfde soort tegels en heeft een rotatiesymmetrie. De vraag is nu: komen wiskundige patronen zoals dat van Penrose ook in de natuur voor? Een kristal dat nooit exact herhaalt maar toch geordend is, wordt een quasikristal genoemd. Alan Mackay berekende dat, als je atomen zou plaatsen op de hoeken van de ruiten in de Penrose-betegeling en hiervan een diffractiepatroon zou meten door er van voren licht door te schijnen, dit diffractiepatroon scherpe pieken zou hebben, met vijfvoudige symmetrie. Dit was heel verrassend omdat je niet, zoals bij normale kristallen, steeds herhalende vlakken met een hogere dichtheid van atomen op precies dezelfde afstand hebt. Tóch zit de informatie van de vijfvoudige symmetrie en de minder harde vorm van ordening kennelijk in het diffractiepatroon. Theoretisch natuurkundige Paul Steinhardt legde uiteindelijk de puzzelstukjes bij elkaar. Hij realiseerde zich dat het kristal van Shechtman een soort driedimensionale Penrose-betegeling was. Hij bedacht het bijbehorende kristalrooster en berekende het diffractiepatroon dat daarbij hoorde. Dit kwam precies overeen met de metingen van Shechtman.. Eindelijk werd duidelijk dat Shechtman écht goed gemeten had.
Hoe nu verder?
Na de bevestiging dat quasikristallen te vinden1 en te maken waren, ontstond een levendig onderzoeksgebied. Onderzoekers wilden de eigenschappen van de quasikristallen berekenen om te zien wat er nog meer bijzonder aan ze was. Denk bij zulke eigenschappen bijvoorbeeld aan het diffractiepatroon, maar ook de elektrische weerstand van de kristallen. Hiervoor moesten nieuwe manieren bedacht worden om eigenschappen te berekenen die al heel lang voor kristallen berekend kunnen worden. Heel veel methoden voor het berekenen van eigenschappen van kristallen berusten er namelijk op dat een kristal uit een herhalend patroon bestaat. Hierdoor kan je eigenschappen voor het hele materiaal snel uitrekenen op basis van alleen de herhalende eenheid, maar het bijzondere aan quasikristallen is zoals we weten juist dat ze níét bestaan uit herhalende eenheden. Dit betekent dat je de eigenschappen van het materiaal als geheel zou moeten berekenen. Een echt materiaal bestaat echter al gauw uit 1023 atomen, dus berekeningen daaraan zijn te groot om te uit te voeren.
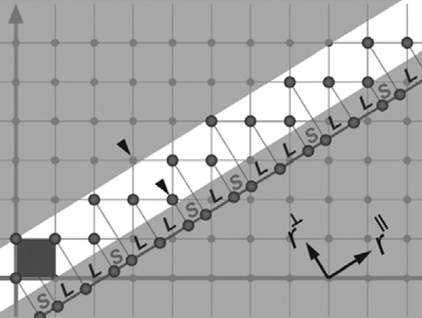
Een van de oplossingen die hierop is bedacht, is de zogenaamde “cut-and-project” methode. De beste manier om die methode te illustreren is door te kijken naar een vierkant rooster. In de afbeelding staat een vierkant rooster met daardoor een lijn getrokken onder een willekeurige hoek. Je kan loodrechte verbindingen tekenen tussen deze lijn en de naastliggende roosterpunten. Waar deze verbindingen de lijn raken worden nieuwe punten geplaatst. Deze punten vormen een eendimensionaal quasikristal, al is dat wellicht moeilijk om je voor te stellen. We noemen deze verzameling van punten op een lijn een eendimensionaal quasikristal, want er zijn steeds afwisselend korte en lange stukjes, maar de volgorde waarin korte en lange stukjes zich afwisselen herhaalt zich nooit. Oftewel: geen herhaling én toch ordening. Dit quasikristal heet de Fibonacciketen, omdat de verhouding tussen de korte en de lange stukjes gelijk blijkt te zijn aan de gulden snede die ook voor de Fibonaccigetallen een belangrijke rol speelt. Je maakt zo dus een eendimensionaal quasikristal door een tweedimensionaal (gewoon) kristal op een eendimensionale lijn te projecteren. Dit blijkt algemeen mogelijk te zijn. Je kan een N-dimensionaal quasikristal maken door een N+1-dimensionaal kristal op een N-dimensionaal ‘hypervlak’ te projecteren.
Dit is niet alleen nuttig voor het genereren van quasikristallen. Elk quasikristal is terug te plaatsen in een normaal kristal in een hogerdimensionale ruimte. Hoeveel dimensies hoger hangt af van het quasikristal. De eigenschappen van dit hogerdimensionale kristal kan je berekenen met de normale methoden die gebruik maken van de herhaling in het kristal. Als je vervolgens de resultaten weer een dimensie omlaag projecteert krijg je de eigenschappen van het quasikristal.
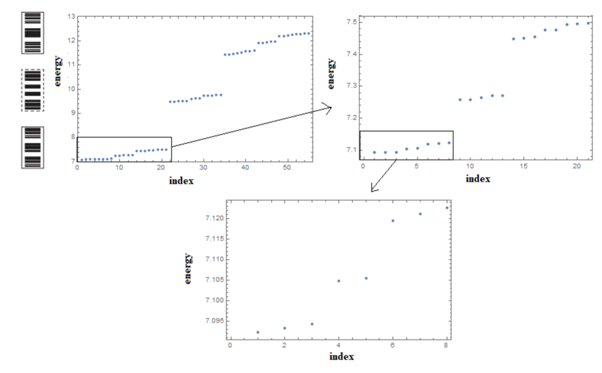
Op deze manier kan je bijvoorbeeld het diffractiepatroon berekenen van een quasikristal. Dit diffractiepatroon heeft veel meer punten dan dat van een normaal kristal, omdat er vanuit een hogere dimensie punten naar beneden geprojecteerd worden. Er kunnen ook veel andere eigenschappen uit berekend worden. Als afsluiter laat ik daarvan de mooiste zien: het spectrum. Het spectrum, ofwel de dispersierelatie, vertelt je hoe de energie van elektronen in een materiaal afhangt van de impuls van de elektronen. Voor quasikristallen is dit spectrum een fractal. Dat betekent dat het er hetzelfde uitziet ongeacht hoe ver je inzoomt. Hieronder zie je het energiespectrum van de Fibonacciketen. Je kan zien hoe het is opgedeeld in drie segmenten, en die drie segmenten zijn weer opgedeeld in drie subsegmenten, enzovoort. Het spectrum vormt een zogenaamde Cantorverzameling, het schoolvoorbeeld van een fractal.
Quasikristallen waren dus een leuke verassing toen onderzoekers eenmaal doorhadden wat ze voor zich hadden. Wat we besproken hebben is nog maar het topje van de ijsberg. Er zijn nog veel meer mooie quasikristallen met verrassende eigenschappen gemaakt (zowel op papier als in chemische labs) en knap bedachte methoden om die eigenschappen te kunnen berekenen. Paul Steinhardt heeft zelfs een heel boek geschreven over zijn zoektocht naar natuurlijk voorkomende quasikristallen, maar dat is een verhaal voor een andere keer.
[1] Er zijn tot nu toe maar twee quasikristallen in de natuur gevonden. De twee gevonden kristallen hebben overigens wel allebei een andere symmetrie.