Door Margot Brouwer en Manus Visser

Duistere krachten
Iets meer dan een maand geleden presenteerde theoretisch natuurkundige Erik Verlinde zijn nieuwe zwaartekrachttheorie. Met die theorie wil hij niet alleen de oorsprong van de zwaartekracht blootleggen, maar ook één van de grootste problemen binnen de kosmologie oplossen. Sterrenkundigen hebben namelijk al halverwege de vorige eeuw ontdekt dat 80% van de massa in het heelal zoek is. (Zie: Donkere materie – Een duistere ontdekking.) Kortweg komt het erop neer dat astronomen al decennia worstelen met het feit dat er meer massa in het universum lijkt te zijn dan ze met hun telescopen kunnen waarnemen.
De hoeveelheid licht die sterrenkundigen observeren van sterren, gas-/stofwolken en andere hemelobjecten, kan worden gebruikt om de massa ervan te bepalen. Door middel van de zwaartekrachtwetten van Newton en Einstein kan men deze massa direct omrekenen naar de hoeveelheid zwaartekracht die deze objecten moeten veroorzaken. Vreemd genoeg is de berekende hoeveelheid zwaartekracht veel te klein om te verklaren waarom de sterren in sterrenstelsels, en ook de sterrenstelsels in clusters, zo snel bewegen. Volgens de huidige gravitatiewetten zouden deze structuren uit elkaar moeten vliegen, omdat er niet genoeg zwaartekracht is om ze bij elkaar te houden.
Hierop hebben astronomen een oplossing bedacht: donkere materie. Als het heelal gevuld is met deze onzichtbare deeltjes, zou dat verklaren waarom er meer zwaartekracht is dan van de materie die we kunnen zien. Inmiddels wordt donkere materie gebruikt om een groot scala aan sterrenkundige waarnemingen te verklaren: niet alleen de bewegingen binnen sterrenstelsels en clusters, maar ook het ontstaan van de grootste structuren in het heelal en de patronen in de kosmische achtergrondstraling. (Zie: Licht in de duisternis.) Het enige probleem is dat, ondanks de decennialange zoektocht, het bijbehorende deeltje nog nooit direct is waargenomen. (Zie: Onzichtbaar en ongrijpbaar.)
Emergente zwaartekracht
Verlinde claimt echter dat zijn nieuwe theorie de missende zwaartekracht ook kan verklaren, zonder het gebruik van onzichtbare deeltjes. In zijn artikel beargumenteert hij dat de wetten van Newton en Einstein de zwaartekracht op grote schaal (denk aan sterrenstelsels en clusters van sterrenstelsels) niet volledig beschrijven. Door dieper na te denken over de oorsprong van zwaartekracht, probeert hij de missende zwaartekracht te verklaren. Volgens Verlinde is zwaartekracht namelijk geen fundamentele kracht, maar is de kracht ‘emergent’, in de zin dat die pas op grote schaal tevoorschijn komt. Het idee dat zwaartekracht emergent is, heeft volgens Verlinde waarneembare gevolgen op kosmologische schaal. (Zie: Emergente zwaartekracht en het donkere heelal.)
Een belangrijk aspect van Verlindes theorie is dat het alle componenten van de totale energie in het heelal met elkaar verbindt. Gewone materie, “donkere materie” en de energie van het vacuüm (ook wel donkere energie genoemd) kunnen niet los van elkaar worden gezien. Kort gezegd wordt het donkerematerie-effect volgens Verlinde veroorzaakt door een wisselwerking tussen gewone materie en de donkere energie. Zonder materie zou die energie homogeen verdeeld zijn over de ruimte. Door de aanwezigheid van materie wordt de donkere energie echter verplaatst, en dat geeft een reactiekracht: het vacuum ‘duwt’ als het ware terug op de materie. Deze reactiekracht zou precies overeen moeten komen met de waarnemingen van donkere materie.
Verlinde heeft dus geen extra donkere materie nodig om het probleem in sterrenstelsels op te lossen, maar de missende zwaartekracht kan wel effectief worden toegekend aan een hoeveelheid schijnbare donkere massa (die dus niet echt bestaat). Een van de belangrijkste resultaten in Verlindes artikel is de relatie tussen deze schijnbare donkere materie en de gewone materie. In formulevorm ziet dat er zo uit:
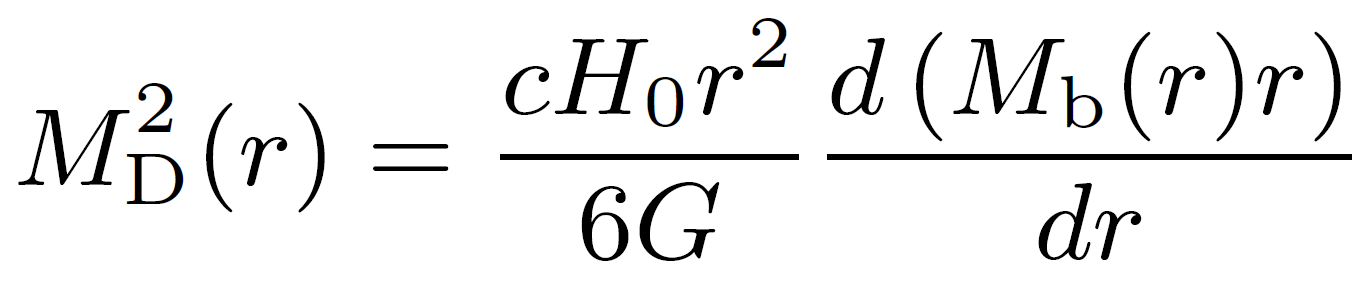
In deze formule is G de zwaartekrachtconstante, r is de afstand tot het centrum van de materieverdeling, MD is de hoeveelheid schijnbare donkere materie, Mb is de massa van de gewone materie, c is de lichtsnelheid, en H0, ten slotte, is de zogenaamde Hubble-constante die aangeeft hoe groot het heelal is. Gegeven een bepaalde hoeveelheid materie Mb, geeft deze formule aan hoeveel schijnbare donkere materie MD er is.
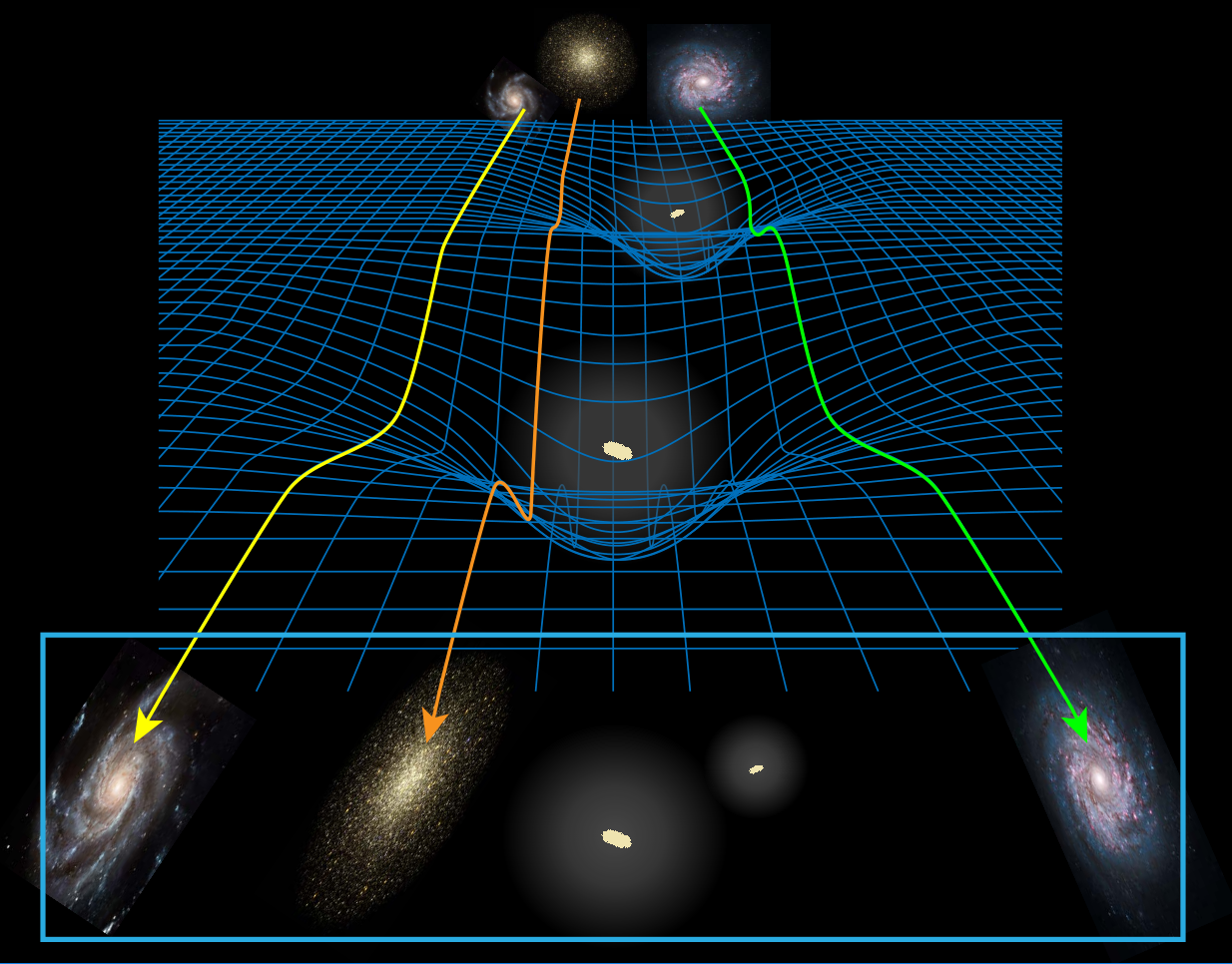
Afbeelding 1. Gravitationele lenswerking.De kromming van de ruimte door de zwaartekracht rondom voorgrondsterrenstelsels buigt het licht van achtergrondsterrenstelsels dat door deze ruimte reist. Door de vervorming van de achtergrondsterrenstelsels waar te nemen met een telescoop, kan de verdeling van zwaartekracht rondom de voorgrondsterrenstelsels worden gereconstrueerd. Afbeelding: APS/Alan Stonebraker; galaxy images from STScI/AURA, NASA, ESA, and the Hubble Heritage Team.
Een eerste test
Als donkere materie inderdaad niet bestaat en zwaartekracht anders werkt, dan zet dit ons hele beeld van het heelal op zijn kop. Maar om erachter te komen of Verlindes nieuwe theorie echt klopt, zal deze uitgebreid moeten worden getest door sterrenkundigen.
Margot Brouwer, een astronoom verbonden aan de Universiteit van Leiden, was al langer geïnteresseerd in Verlindes theorie. Een jaar geleden zag ze de formule hierboven voor het eerst tijdens een lezing van Verlinde, en besloot ze deze aan een test te onderwerpen. Samen met haar team doet ze namelijk onderzoek naar de verdeling van zwaartekracht rondom sterrenstelsels. Deze verdeling kan worden gemeten omdat, volgens Einsteins algemene relativiteitstheorie, zwaartekracht een effect is van de kromming van de ruimte.
Stel dat we met onze telescoop in de richting van twee sterrenstelsels kijken. In Figuur 1 zijn deze sterrenstelsels te zien als gele vlekjes, met daaromheen de gekromde blauwe lijnen, die de ruimte weergeven. Ver achter deze sterrenstelsels staan een paar achtergrondsterrenstelsels. Het licht van de achtergrondsterrenstelsels reist door de gekromde ruimte. Hierdoor zien we deze sterrenstelsels vervormd door onze telescoop. Dit effect heet de lenswerking van zwaartekracht, omdat de zwaartekracht het licht net als een lens afbuigt. De vervorming van de achtergrondsterrenstelsels geeft dus aan waar de zwaartekracht zich bevindt. Omdat de lenswerking van zwaartekracht erg zwak is, zijn er niet één of twee, maar duizenden voorgrondsterrenstelsels (met miljoenen achtergrond-sterrenstelsels) nodig om dit effect nauwkeurig te meten. Daarom hebben de astronomen de gemiddelde zwaartekrachtverdeling rondom 33.613 voorgrondsterrenstelsels gemeten.
De voorgrondsterrenstelsels zijn waargenomen met de GAMA survey (Galaxy And Mass Assembly), een samenwerkingsverband dat met de Anglo-Australian Telescope (AAT) zeer nauwkeurig de afstand en eigenschappen van tienduizenden sterrenstelsels heeft bepaald. De vervorming van de achtergrondsterrenstelsels is zeer nauwkeurig waargenomen met de Kilo-Degree Survey, die wordt uitgevoerd met de Very Large Survey Telescope (VST). Deze telescoop staat op de 2,6 kilometer hoge berg Cerro Paranal in Chili (te zien in afbeelding 2), en is speciaal ontworpen om de lenswerking van zwaartekracht waar te nemen.

Afbeelding 2. Very Large Survey Telescope.Het Paranal-observatorium in Chili. De Very Large Survey Telescope, waarmee de verdeling van zwaartekracht is waargenomen, staat op de grote berg vooraan, net achter de vier telescopen van de Very Large Telescope. Foto: J.L. Dauvergne & G. Hüdepohl (atacamaphoto.com)/ESO
De resultaten
Het eindresultaat van de test is te zien in afbeelding 3. De vier panelen geven het resultaat weer voor sterrenstelsels van verschillende ‘gewone’ massa, van de laagste naar de hoogste massa. Met gewone massa bedoelt men die van de normale lichtgevende materie in de sterrenstelsels, zoals de sterren en het gas. De zwarte punten (met foutenbalken) in elk van de vier grafieken laten de gemeten hoeveelheid zwaartekracht rondom het sterrenstelsel zien (op de y-as), als functie van de afstand tot het centrum van het sterrenstelsel (op de x-as). De punten gaan omlaag naarmate de afstand toeneemt, omdat de zwaartekracht dichter bij het sterrenstelsel sterker is dan verder weg.
De afstand tot het sterrenstelsel (de x-as) is te zien op logaritmische schaal, en wordt gemeten in kiloparsec, of kpc. Eén kpc is ongeveer 3000 lichtjaar. De meting begint bij een afstand van 30 kpc en loop door tot 3000 kpc van het sterrenstelsel. Het is belangrijk om op te merken dat een gemiddeld sterrenstelsel een straal heeft van ongeveer 30 kpc (zo’n honderdduizend lichtjaar). Dit betekent dat de meting pas begint bij de rand van het sterrenstelsel, en doorgaat tot een afstand die wel honderd keer zo groot is als het sterrenstelsel zelf. De zwaartekracht die hier gemeten wordt, bevindt zich dus ver buiten de plek waar de gewone lichtgevende materie, zoals de sterren en het gas, zich bevindt. Er moet daarom iets anders zijn dat deze zwaartekracht veroorzaakt: donkere materie óf een nieuwe kijk op zwaartekracht.
De gekleurde lijnen laten de voorspellingen zien van deze twee mogelijkheden. De rode lijn komt overeen met het meest gebruikte model voor de verdeling van donkere materie rondom sterrenstelsels: het Navarro-Frenk-White model, genoemd naar de drie bedenkers. Dit model kan de gemeten verdeling van zwaartekracht goed verklaren, maar er zit een addertje onder het gras. Donkere materie is namelijk onzichtbaar, waardoor je van tevoren niet kunt weten hoeveel donkere materie er rond een sterrenstelsel zit. De massa van de donkere materie moet daarom worden aangepast om het model te laten kloppen met de data: dit wordt in de natuurkunde een “vrije parameter” genoemd.
De blauwe lijnen komen overeen met de zwaartekrachtverdeling die gegeven wordt door Verlindes theorie van emergente zwaartekracht. Omdat in Verlindes theorie geen donkere materie bestaat, wordt alle zwaartekracht veroorzaakt door de normale materie: de sterren en het gas in de sterrenstelsels. Om de zwaartekrachtverdeling in Verlindes theorie te bepalen, moet er dus eerst een model gemaakt worden voor sterrenstelsels. Het eenvoudigste model is om aan te nemen dat het sterrenstelsel zo klein, dat het in vergelijking met de schaal van de meting een puntdeeltje is. Je doet dan alsof alle massa geconcentreerd zit in één punt. Dit eenvoudige model moet natuurlijk gecontroleerd worden. Daarom hebben Brouwer en haar collega’s ook een complex model gemaakt, dat de volledige massaverdeling beschrijft van de sterren, het koude en hete gas, en eventuele satelliet-sterrenstelsels die zich rondom het sterrenstelsel kunnen bevinden. De zwaartekrachtverdeling van de puntmassa en het complexe model zijn beide te zien in afbeelding 3, maar er is weinig verschil tussen de twee modellen. Het puntmassa-model is dus nauwkeurig genoeg.
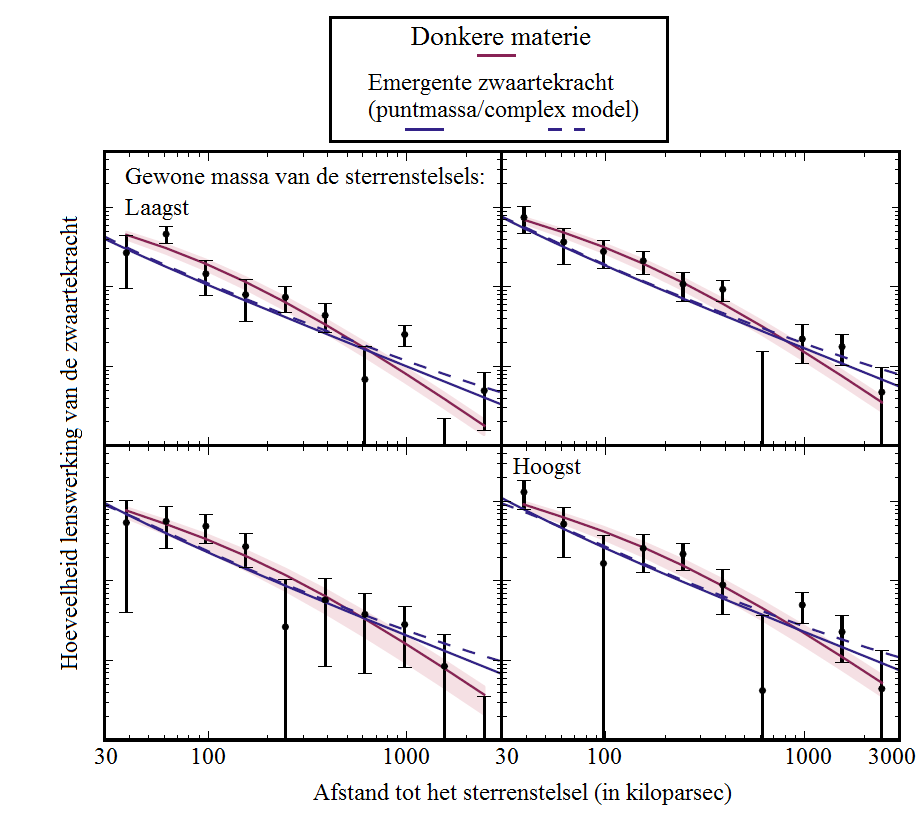
Figuur 3. Resultaten van de test.In deze grafiek worden het model van donkere materie én Verlindes theorie vergeleken met de gemeten verdeling van zwaartekracht rondom sterrenstelsels van vier verschillende massa’s. Beide modellen presteren goed, maar Verlindes theorie doet dit zonder vrije parameters. Afbeelding: Margot M. Brouwer et al. 2016 (arXiv:1612.03034)
Kosmisch gelijkspel
Hoe doorstaat Verlindes theorie de vergelijking met de data? Ook emergente zwaartekracht blijkt de data goed te beschrijven, maar net iets minder goed dan de donkere materie. Omdat de hoeveelheid zwaartekracht in Verlindes theorie echter direct voorspeld kan worden uit de zichtbare massa (die we kunnen meten) heeft dit model geen vrije parameters. De blauwe lijn geeft een directe voorspelling, waardoor Verlindes theorie weer een streepje voor heeft op het model van donkere materie. Hierdoor kun je zeggen dat Verlindes model weer beter presteert. Uiteindelijk is het voor deze meting gelijkspel.
Het feit dat emergente zwaartekracht deze specifieke meting zonder vrije parameters kan verklaren is interessant, maar natuurlijk nog geen reden om het hele idee van donkere materie van tafel te vegen. Er zijn verschillende waarnemingen die Verlindes theorie (nog) niet kan verklaren. Deze theorie is alleen nog doorgerekend voor bolvormige, statische, geïsoleerde massaverdelingen, maar in het heelal bevinden zich talloze objecten die niet aan die eisen voldoen. De beroemde “Bullet Cluster” bijvoorbeeld, waarin twee groepen van sterrenstelsels op elkaar botsen, is zeer dynamisch en kan dan ook nog niet worden aangepakt met Verlindes theorie. (Zie ook: Strijd tussen de sterren.) Ook het beschrijven van de meting van de eerste dichtheidsverdelingen in het vroege universum, en de daaropvolgende vorming van grote structuren in het heelal, worden nog een zware kluif voor Verlindes theorie. Al met al is er dus nog een lange weg te gaan, maar deze eerste meting geeft in elk geval stof tot nadenken.
Bibliografie
1. Emergent Gravity and the Dark Universe – Erik P. Verlinde 2016 (arXiv:1611.02269)
2. First test of Verlinde’s theory of Emergent Gravity using Weak Gravitational Lensing measurements – Margot M. Brouwer et al. 2016 (arXiv:1612.03034)
Geaccepteerd voor publicatie in het Britse vakblad Monthly Notices of the Royal Astronomical Society.