Biljarten: een wiskundig mysterie
Een geïdealiseerde versie van het biljartspel fascineert wiskundigen al decennialang. De onderliggende vraag is heel eenvoudig: als je een biljartbal wegstoot, waar gaat die dan naartoe en waar zal de bal eindigen? Neem daarbij aan dat het biljart perfect is: de banden weerkaatsen de bal perfect, er bevinden zich geen obstakels op de tafel, de beweging is wrijvingsloos, enzovoort. De bal zal dan nooit ergens ‘eindigen’: de beweging gaat altijd maar door. Maar komt de bal ooit terug waar hij begonnen is? Komt hij uiteindelijk langs elk deel van de tafel? En als we de richting van de bal of het startpunt een heel klein beetje veranderen, lijkt de nieuwe baan dan op de oude?
Vanuit een wiskundig oogpunt blijken al deze vragen enorm intrigerend. De antwoorden zijn vaak niet bekend – zeker als de vorm van het biljart niet zo eenvoudig is als een vierkant of rechthoek. Voor driehoekige biljarttafels met hoeken van minder dan 100 graden is bijvoorbeeld nog bekend dat er altijd periodieke banen zijn: trajecten die de bal aflegt en die zichzelf uiteindelijk herhalen. Je kunt dat wiskundig bewijzen. Maak nu echter een van de hoeken een klein beetje groter, en geen enkele wiskundige weet het antwoord meer.
Het geïdealiseerde biljartspel is niet alleen een favoriete vrijetijdsbesteding van wiskundigen. Het idee speelt ook een belangrijke rol in de natuurkunde en andere wetenschappen. Veel van de vragen over biljarten kunnen namelijk geformuleerd worden als vragen over chaos: leiden kleine verschillen in de begincondities van een systeem – of het nu een bal op een biljarttafel, een molecuul in een gas of een vogel in een zwerm is – ook tot kleine verschillen in de eindsituatie?
Een nieuwe regel
In hun onderzoek, uitgevoerd aan de Universiteit van Amstedam, ontdekten natuurkundigen dat een kleine aanpassing aan de regels van het geïdealiseerde biljartspel het aantal toepassingen in de wereld om ons heen nog vergroot. Mazi Jalaal, mede-auteur van de publicatie en groepsleider van de onderzoeksgroep waar het onderzoek werd uitgevoerd, licht toe: “In de natuur hebben veel levende organismen een externe vorm van geheugen. Ze laten bijvoorbeeld sporen achter om te onthouden waar ze geweest zijn. Met die informatie kunnen ze ofwel dezelfde route nog eens volgen, ofwel – als ze bijvoorbeeld op zoek zijn naar voedsel – datzelfde gebied juist niet nog eens bezoeken.”
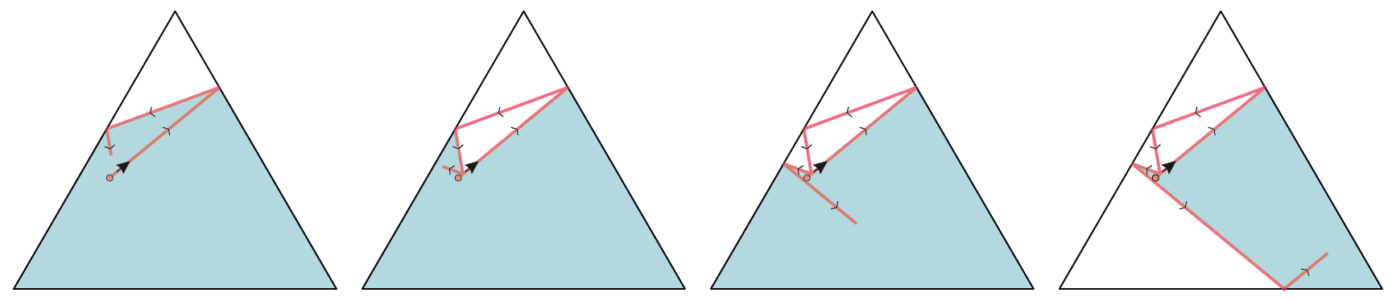
Die laatste mogelijkheid bracht de onderzoekers tot een interessant idee: wat als we nu eens een regel aan het biljartspel toevoegen, namelijk dat de bal nooit zijn eigen afgelegde weg mag kruisen? Het resultaat – zie de afbeelding hieronder – is dat het effectieve oppervlak van de biljarttafel steeds kleiner wordt. Het is zelfs zo dat de bal uiteindelijk door zijn eigen spoor op één punt ‘gevangen raakt’.
Intrigerende nieuwe vragen
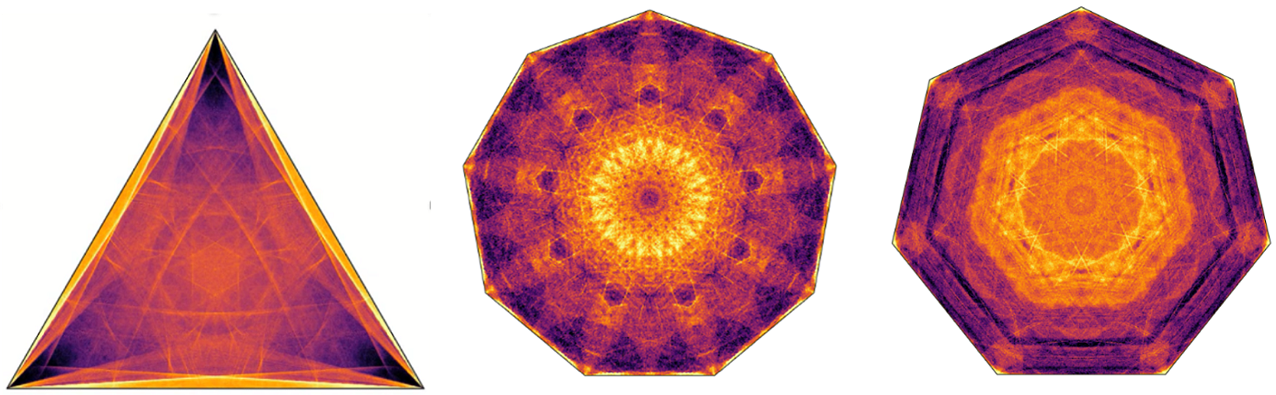
Dat de bal zo een eindpunt bereikt, maakt het systeem alleen maar intrigerender. Zelfs eenvoudige vragen worden nu fascinerende problemen. Welke afstand legt de bal bijvoorbeeld af voor hij gevangen wordt? Het antwoord hangt af de vorm van de tafel, maar vooral van het startpunt en de richting van de bal. Soms legt de bal een afstand af die maar een paar keer de lengte van de tafel is, soms kan de bal wel 100 keer die lengte afleggen voordat hij gevangen wordt. Wáár de bal eindigt is ook een ingewikkeld vraagstuk: als je het experiment met een computer miljoenen keren herhaalt, steeds met net iets andere beginpunten en -snelheden, vind je prachtige patronen in de eindtoestanden.
De afbeelding bovenaan deze tekst toont enkele voorbeelden van zulke patronen. Een interessant verschijnsel is dat deze dynamische systemen ook chaotisch zijn. Verander de beginpositie of -snelheid van de zichzelf mijdende bal een klein beetje, en je kunt een totaal ander eindpunt op het biljart vinden. Daarbovenop tonen de afbeeldingen dat niet elk eindpunt even waarschijnlijk is – en daarin verschilt de zichzelf mijdende bal van de gewone biljartbal. Sommige gebieden fungeren veel vaker als eindstation dan andere. Wiskundigen zullen er nog heel wat werk aan hebben om al die observaties te kunnen verklaren en bewijzen.
Eindeloos veel toepassingen
Interessant is dat de twee eerste auteurs van de publicatie allebei masterstudenten zijn. Mazi Jalaal zegt daarover: “Het idee van een ‘biljart met geheugen’ is eenvoudig genoeg én nieuw genoeg, zodat er geen jaren ervaring nodig zijn om het te bestuderen. Thijs en Stijn hebben geweldig werk verricht door zich het materiaal eigen te maken en slimme manieren te bedenken om al deze nieuwe open vragen te bestuderen. Ik ben heel blij dat ze nu al eerste auteurs van een publicatie kunnen zijn.”
De resultaten zijn slechts de eerste stappen op weg naar wat een geheel nieuw onderzoeksgebied zou kunnen worden. Er zijn niet alleen allerlei interessante wiskundige vragen die nu op een antwoord wachten; de toepassingen in de natuurkunde – waaronder de biofysica – zijn ook eindeloos. Jalaal: “Het idee van ‘gevangen raken’ smeekt om verder onderzoek, ook in echte systemen in de natuur. We weten bijvoorbeeld dat eencellige slijmzwammen zichzelf mijdende trajecten gebruiken. Raken die ook gevangen, en wat gebeurt er dan? Of hebben ze slimme mechanismes om dat te voorkomen? Gebruiken ze zulke mechanismes als een nog betere strategie in hun zoektocht naar voedsel? De resultaten van dit onderzoek kunnen ons helpen om zulke biologische systemen beter te begrijpen, en mogelijk kunnen we die lessen ook weer toepassen om deze vorm van ‘biljarten met geheugen’ te optimaliseren en bijvoorbeeld te gebruiken in robots.”
Publicatie
Billiards with Spatial Memory, Thijs Albers, Stijn Delnoij, Nico Schramma en Maziyar Jalaal, Physical Review Letters 132 (2024) 157101.