Een hologram is een tweedimensionale afbeelding die er driedimensionaal uitziet – zó driedimensionaal dat je door de afbeelding te draaien daadwerkelijk het gevoel krijgt dat je om een ruimtelijk object heen beweegt.
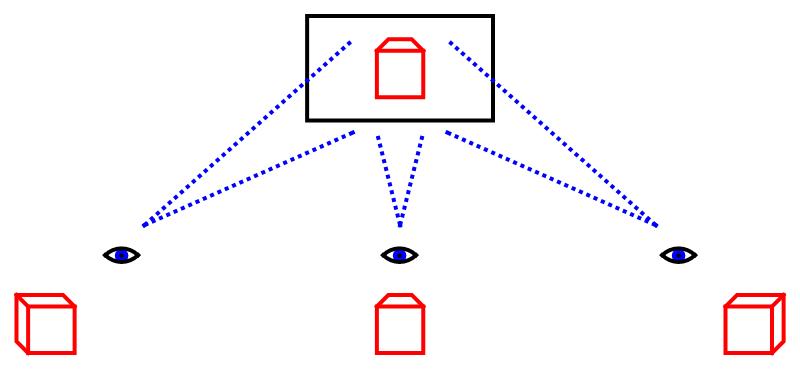
Afbeelding 1. Een hologramEen schets van een hologram. Het hologram is tweedimensionaal, maar bevat toch driedimensionale informatie. Als we onder verschillende hoeken naar de afbeelding kijken, zien we een verschillend beeld.
Een hologram is niet echt driedimensionaal: het is een tweedimensionale afbeelding die informatie bevat over een driedimensionaal object. Afhankelijk van de hoek waaronder we naar het hologram kijken, komt een ander deel van die informatie op ons netvlies terecht.
Holografie, het maken van zulke hologrammen, is een erg interessant vakgebied waarbij de nodige natuurkunde komt kijken – maar dat is niet het onderwerp van dit dossier. Dit dossier gaat over een verschijnsel in de theoretische natuurkunde waarin een bepaald systeem zich net als een hologram gedraagt. Hoewel zo’n systeem bijvoorbeeld driedimensionaal is, en dus met driedimensionale wiskunde beschreven kan worden, blijkt er ook een beschrijving van het systeem te zijn in termen van tweedimensionale wiskunde. Met andere woorden: we kunnen twee lijstjes natuurwetten opstellen, waarvan het op het eerste gezicht lijkt alsof het ene een driedimensionaal systeem beschrijft, en het andere een tweedimensionaal systeem. Als we beter kijken, blijkt echter dat we op twee totaal verschillende manieren precies hetzelfde systeem beschrijven. Op de ene manier bekeken is zo’n systeem tweedimensionaal, op de andere manier driedimensionaal.
Het aantal dimensies hoeft daarbij niet altijd twee en drie te zijn; in de theoretische natuurkunde kennen we ook allerlei systemen die vier- of hoger-dimensionaal zijn. In het algemeen kan het gebeuren dat een X-dimensionaal systeem uiteindelijk ook beschreven kan worden als een Y-dimensionaal systeem, waarbij Y groter of kleiner is dan X. We noemen zulke beschrijvingen duaal, en in al deze gevallen (ook als het verschil in dimensies groter is dan één) spreken we van “holografie”. Het is deze vorm van holografie waar we in dit dossier dieper op in zullen gaan.
Het idee van holografie is afkomstig uit de fysica van zwarte gaten. Als we de thermodynamische eigenschappen van een driedimensionaal zwart gat bestuderen, ontdekken we al snel dat die eigenschappen zich gedragen alsof het zwarte gat een tweedimensionaal systeem is. In zekere zin is het alsof alle fysica die zich in het zwarte gat afspeelt, ook beschreven kan worden met behulp van natuurwetten die alleen op het oppervlak van het zwarte gat gedefinieerd zijn.
Dat is op zich een opmerkelijk feit, maar lange tijd leek het erg lastig om het idee van holografie preciezer te maken. Niemand had enig idee hoe de duale natuurwetten er in een lager aantal dimensies precies uit zouden zien. Dat veranderde in 1997, toen de Argentijn Juan Maldacena een artikel publiceerde waarin hij expliciet twee duale beschrijvingen van hetzelfde systeem gaf. Dit systeem was in zekere zin nog niet erg fysisch: Maldacena beschreef een heel symmetrisch zwart gat in vier ruimtedimensies (dus één meer dan in onze werkelijke natuur), met behulp van duale natuurwetten in drie ruimtedimensies. Al snel bleek de beschrijving van Maldacena echter het topje van een ijsberg, en op den duur werden er ook allerlei duale beschrijvingen gevonden van systemen die de fysische werkelijkheid beter benaderen.

Afbeelding 2. Juan Maldacena
Een steeds terugkerend thema in al deze voorbeelden van holografie is de zwaartekracht. De algemene les lijkt te zijn dat vrijwel elk systeem waarin de zwaartekracht een rol speelt, zoals bijvoorbeeld een zwart gat, ook beschreven kan worden op een duale, lagerdimensionale manier waarin de zwaartekracht geen rol speelt. Dit leidt direct tot een bijzonder nuttige toepassing van de holografie, aangezien we van zwaartekrachtstheorieën – zeker wanneer die zich op quantummechanische schaal afspelen – lang niet altijd alles begrijpen. In zo’n geval kunnen we de duale theorie dus gebruiken om van alles te leren over het zwaartekrachtssysteem.
In de rest van dit dossier zullen we nauwkeuriger beschrijven hoe de fysica van zwarte gaten leidt tot het idee van holografie, en hoe dit idee tegenwoordig in de natuurkunde gebruikt wordt. Op dit moment (voorjaar 2015) zijn we bezig met het afronden van enkele andere dossiers; het eerste artikel uit het dossier “holografie” zal naar verwachting in de tweede helft van 2015 op deze website verschijnen.