Een vergeten genie
De fascinerende Michell, die werd geboren op kerstdag 1724 in een bescheiden gehucht in het Engelse Nottinghamshire, heeft ondanks zijn rijke carrière in de Anglicaanse Kerk en aan de universiteit van Cambridge nooit veel tijd besteed aan het promoten van zijn briljante ideeën. Nochtans heeft eerwaarde Michell op essentiële wijze de loop van de wetenschappelijke geschiedenis beïnvloed, en dat op gebieden gaande van geologie via magnetisme tot astronomie. Zijn seismologische modellen en technieken om kunstmatige magneten te maken zijn indrukwekkend, maar vooral zijn inbreng op het vlak van zwaartekracht was zijn tijd ver vooruit en spreekt zonder meer tot de verbeelding.

Afbeelding 1. Henry Cavendish.Schets en handtekening van Henry Cavendish (1731-1810). Afbeelding: George Wilson.
Henry Cavendish (afbeelding 1) is een naam die wetenschapsliefhebbers wél zullen beantwoorden met een knikje van herkenning. De chemicus en natuurkundige was een persoonlijke vriend en collega-wetenschapper van Michell, en heeft een belangrijk deel van zijn faam te danken aan het vergeten genie. Het voornaamste fysisch experiment dat Cavendish’ naam draagt, is de eerste precieze meting van de gemiddelde massadichtheid van de aarde. Om die waarde te achterhalen, moest hij eerst de notoir moeilijk te bepalen grootte – of beter ‘kleinte’ – van de universele gravitatieconstante G te weten komen. Het is voornamelijk dàt resultaat waarvoor het ‘Cavendishexperiment’ als mijlpaal in de experimentele natuurkunde beschouwd wordt. Zijn resultaat week slechts 1% af van het huidig aanvaard getal; indrukwekkend!
De meetopstelling is zo eenvoudig als ze briljant is: meet aan de hand van een uiterst gevoelige torsiebalans (afbeelding 2) simpelweg het effect van gravitationele aantrekking tussen (letterlijk) loodzware ballen op de uitwijking van die ballen. Zowel het idee als het volledig uitgewerkt ontwerp van dit experiment was van de hand van John Michell, die eind april 1793 overleed, nog voor hij het nauwkeurig uitgeschreven plan zelf kon verwerkelijken. Aan plagiaat heeft Cavendish zich gelukkig niet schuldig gemaakt: hij liet het niet na Michells wezenlijke bijdrage te erkennen.
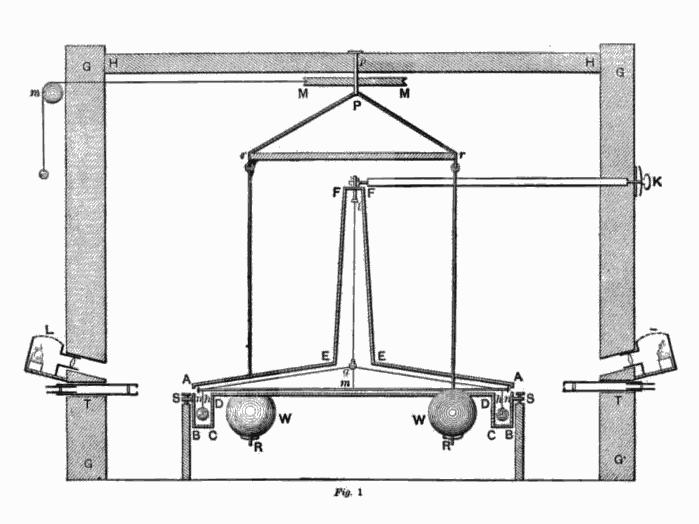
Afbeelding 3. Het Cavendishexperiment.Verticale doorsnede van de opstelling van het Cavendishexperiment. Een paar grote en een paar kleine loden ballen zijn vrij van elkaar opgehangen. De afbeelding is gemaakt door Cavendish zelf.
Naast de cruciale voorzet te geven voor deze experimentele doorbraak, blijkt uit Michells correspondentie met Cavendish eveneens een bijzondere aanleg van de eerwaarde voor theoretisch begrip van zwaartekrachttheorie. In een brief die Michell hem gisteren, op 27 november, precies 234 jaar geleden verstuurde, vermeldt hij voor het eerst een berekening waarin hij het bestaan van zwarte gaten voorspelt. Dat, uiteraard, zonder enige kennis van Einsteins algemene relativiteitstheorie (1915), maar volstrekt in de taal van de newtoniaanse mechanica. Erg opvallend! Wat moeten we ons daarbij voorstellen?
Donkere sterren
Met zijn zelfgebouwde telescoop tuurde Michell geregeld naar de nachtelijke hemel boven het vreedzame Cambridge, waar hij nauwgezet de catalogus van bekende sterren aanvulde. Door middel van een sterk staaltje statistiek, toen nog een erg nieuw domein, kon hij uit die catalogus afleiden dat veel sterren in rond elkaar dansende paren moeten voorkomen. Deze waarneming van een kosmische overvloed aan zogenaamde dubbelsterren is op zich al noemenswaardig, al is het maar om de universaliteit van de onderlinge aantrekkingskracht van massieve objecten te bevestigen, maar Michell ging nog een stap verder. Zouden we niet, zo redeneerde hij, bewegingen van bepaalde sterren kunnen interpreteren als de dynamiek van een dubbelster, waarbij een van de twee sterren geen licht kan uitstralen – een onzichtbare, donkere ster, dus? Zo’n ‘gekke beweging’ van een enkele ster rond een onzichtbaar punt was een te klein effect om met 18de-eeuwse telescopen waar te nemen, maar is tegenwoordig een belangrijke experimentele methode om dergelijke donkere objecten te identificeren. Een sterk gedachte-experiment dus, dat leidde tot een intrigerend betoog voor de theoretische mogelijkheid dat zo’n donkere begeleiderster zou bestaan. De redenering gaat als volgt.
Ten eerste: zwaartekrachttheorie zoals uiteengezet door Newton kende voor Michell geen geheimen, en in het bijzonder begreep hij van het concept ‘ontsnappingssnelheid’ de consequenties erg goed. Deze term duidt de snelheid aan die een massief voorwerp moet hebben om te kunnen ontsnappen aan de greep van een zwaartekrachtveld. De formule luidt als volgt:
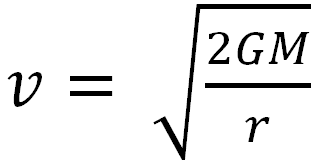
waarbij G de universele gravitatieconstante is, M de massa van het object dat het zwaartekrachtveld opwekt, en r de straal daarvan. Een concreet voorbeeld brengt hier meer inzicht: als een tennisbal zich voor eeuwig wil bevrijden van de gravitationele invloed van de aarde, heeft die vanaf het aardse oppervlak een snelheid nodig van ruim 40 000 km/u! (Vul om dit antwoord zelf te vinden als waarden in de formule hierboven maar de aardse straal en massa en de waarde van G in.)
Laat ons nu eens ten tweede, bedacht Michell zich, in plaats van de aarde een hemellichaam voorstellen waarvan de straal en de massa zulke waarden hebben dat de ontsnappingssnelheid groter wordt dan de lichtsnelheid. Het leek hem redelijk aan te nemen dat licht uit deeltjes bestaat die op dezelfde manier door zwaartekracht worden beïnvloed als eender welk object. Een ‘massaloos deeltje’ heeft binnen de newtoniaanse mechanica immers geen betekenis, en van lichtgolven was nog geen sprake tot Young in 1801 zijn bekende tweespletenexperiment deed. Mocht er met andere woorden een ster bestaan waarbij de ontsnappingssnelheid groter is dan de snelheid c waarmee de lichtdeeltjes het oppervlak van de ster verlaten, dan kunnen die lichtdeeltjes nooit voldoende energie hebben om de aarde te bereiken, en dus gezien te worden. Al het sterlicht zit gevangen. Michell rekende het uit voor Cavendish, maar ga het vooral zelf na: een object met minstens vijfhonderd keer de straal van de zon, maar met dezelfde massadichtheid, zou aanspraak maken op de titel donkere ster, schrijf hij. In essentie voorspelde hij hier de voornaamste eigenschap van wat we nu een zwart gat noemen.
Een merkwaardige overeenkomst
De wetenschap is in de eeuwen na Michell niet blijven stilstaan. Met name door Einsteins grensverleggend werk weten we nu veel beter wat de manier is waarop zwaartekracht zich manifesteert, hoe die zich verhoudt tot de geometrie van de ruimtetijd en hoe die kracht zelfs massaloze deeltjes stuurt. Karl Schwarzschild (afbeelding 3), de Duitser wiens naam aan het begin van het artikel ook reeds gevallen is, ging meteen met Einsteins berekeningen aan de slag om in essentie dezelfde vraag als Michell te stellen, maar dan met een geüpdatet wiskundig wereldbeeld. Om de vraag of er in de kosmos ook werkelijk objecten bestaan waaraan zelfs licht niet kan ontsnappen, maakte Schwarzschild zich niet druk. Wel rekende hij met Einsteins formalisme uit dat indien iets dergelijks zou bestaan, de straal van zo’n hemellichaam maximaal de zogenaamde Schwarzschildstraal kan zijn, gedefinieerd als
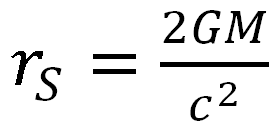
Dit is de straal van de pikzwarte bol die we ons voorstellen als we aan een zwart gat denken, en is bovendien exact de straal die je krijgt wanneer je in de eerste formule hierboven eist dat de ontsnappingssnelheid precies de lichtsnelheid is: v = c. Opmerkelijk is dat: de newtoniaanse theorie, een benadering die allang tegen zijn beperkingen aangelopen zou moeten zijn voor de beschrijving van een zwart gat, geeft toch hetzelfde resultaat voor de straal als de rigoureuze en dieper gemotiveerde berekening binnen de algemene relativiteitstheorie. Niet bijna hetzelfde, maar exact. Onderzoeken waarom dat zo is, zou ons te ver voeren, maar dat het eigenaardig is, staat buiten kijf.

Afbeelding 3. Karl Schwarzschild.Karl Schwarzschild (1873-1916).
Natuurlijk zijn er ook belangrijke verschillen tussen Schwarzschilds zwarte gaten en Michells donkere sterren. Ten eerste is rs werkelijk een point of no return binnen de algemene relativiteitstheorie: een deeltje dat deze denkbeeldige grens gepasseerd is, heeft volstrekt geen kans er ooit nog uit te ontsnappen. Anderzijds kan in Michells benadering (bijvoorbeeld) een lichtdeeltje wel even de donkere ster verlaten; het moet eenvoudigweg binnen een eindige tijd terugkeren richting de ster, zoals wanneer je een tennisbal vanaf de grond omhoog gooit en terug opvangt.
Ten tweede is er binnen het newtoniaans paradigma geen reden om aan te nemen dat deeltjes niet tot voorbij de lichtsnelheid versneld kunnen worden. Die superluminaire deeltjes zouden dan natuurlijk wel aan de klauwen van het zwaartekrachtveld kunnen ontkomen. De speciale relativiteitstheorie leert ons evenwel dat dit scenario niet fysisch kan zijn.
Ten slotte kunnen we nog vermelden dat voor andere fenomenen de effecten van algemene relativiteitstheorie zich wél manifesteren. De mate waarin een lichtstraal die een zwart gat passeert, wordt afgebogen, bijvoorbeeld, is in werkelijkheid tweemaal sterker dan Michell voorspeld zou hebben.
Onthoud de naam
De theoretische mogelijkheid voor een donkere ster was geen eenmalig voorstel in de geschiedenis van de newtoniaanse natuurkunde. In 1796, dertien jaar na Michells briefwisseling met Cavendish, besprak Pierre-Simon Laplace dezelfde probleemstelling op onafhankelijke wijze. Het heeft tot in de jaren zeventig van de vorige eeuw geduurd totdat boven water kwam dat, indien we eerlijk willen zijn, we de pluim van Laplace’ hoed naar die van onze Engelse geestelijke moeten verplaatsen. Op meer en meer vlakken binnen de natuurkunde wordt eerwaarde John Michell uit de plooien van de geschiedenis gevist om hem op een ereplaats tussen de wetenschappelijke grootmachten te plaatsen, en dat vinden wij zeker terecht.
Afbeelding blokkenschema: een computerberekening toont hoe Michells “donkere sterren” er volgens de algemene relativiteitstheorie uit zien. Afbeelding: Ute Kraus en Axel Mellinger (CC BY-SA 2.5).