Donkere materie (1): Een duistere ontdekking

Met bovenstaand citaat beschrijft het wereldberoemde wetenschappelijke tijdschrift Nature in weinig woorden een van de grootste problemen in de moderne kosmologie. In de loop van de afgelopen honderd jaar hebben astronomen steeds meer bewijzen gevonden voor een heelal waarin alle materie die we kennen – sterren, planeten, gas, stof, en zelfs exotische objecten zoals zwarte gaten en neutrino’s – slechts 20% van alle massa verklaart. De overige 80% bestaat volgens de meeste astronomen uit een onbekend en onzichtbaar soort deeltje dat “donkere materie” genoemd wordt.

Deze mysterieuze substantie straalt geen licht uit en absorbeert het ook niet; het heeft er eigenlijk geen enkele invloed op. Kortom, de op licht gebaseerde waarnemingen waar de astronomie van alle tijden van afhankelijk is (van de oude Babyloniërs tot de modernste ruimte-telescopen) zullen ons bij dit probleem niet helpen. Sterker nog, voor zover de huidige waarnemingen hebben kunnen vaststellen, heeft donkere materie op bijna geen enkele manier wisselwerking met onze normale, zichtbare materie. Dit maakt het ongelofelijk moeilijk om donkere materie te onderzoeken. Maar, als donkere materie zo onzichtbaar is, hoe weten we dan dat ze bestaat? En als die materie bijna niets doet, hoe wordt er dan onderzoek naar gedaan? Dat is, onder andere, waar dit dossier over donkere materie in de komende artikels antwoord op wil geven. In dit eerste artikel bespreken we hoe het kan dat donkere materie, ondanks haar onzichtbare aard, is ontdekt.

Zware kost

Donkere materie is eigenlijk niet één keer, maar meerdere keren op verschillende manieren ontdekt, wat astrofysici steeds sterker van dit probleem heeft overtuigd. Al deze ontdekkingen hangen echter met één concept samen: de zwaartekracht. De zwaartekracht is, voor zover we weten, de enige manier waarop donkere materie met zichtbare materie wisselwerkt, en dit is ook de manier waarop astronomen zulke materie hebben ontdekt. De wetten van de zwaartekracht zijn namelijk al in 1687 beschreven door Isaac Newton, en in 1915 verbeterd door Albert Einstein. Door middel van deze zwaartekrachtwetten kunnen fysici precies uitrekenen hoeveel kracht twee massa’s op elkaar uitoefenen, en welke bewegingen daarop moet volgen.

Zo hebben astrofysici door het bestuderen van de beweging van zichtbare materie, zoals sterren en gas, kunnen ontdekken dat er meer massa moet zijn dan we kunnen zien. Een groot verschil tussen de verscheidene ontdekkingen is echter de schaal: de effecten van donkere materie zijn op veel verschillende lengteschalen waargenomen, van zeer nabije sterren tot en met de structuur van het gehele heelal. In dit artikel beginnen we bij de kleinste schaal, waar donkere materie ook historisch het eerst ontdekt is.

Afbeelding 1. Vera Rubin.Vera Rubin observeerde de rotatiekrommen van tientallen sterrenstelsels, en bevestigde daarmee onomstotelijk dat de zichtbare massa in sterrenstelsels niet groot genoeg is om hun rotatiesnelheden te verklaren. Bron: Dr. Rubin (1970)

Sterren, sterrenstelsels en clusters

Eén van de eersten die het bestaan van onzichtbare massa opmerkte was de Nederlandse astronoom Jan Hendrik Oort. In 1932 bestudeerde hij de bewegingen van naburige sterren, en concludeerde dat de massa in ons deel van de Melkweg groter moet zijn dan die van waargenomen sterren en gas. Zijn berekeningen bleken echter onvoldoende bewijs. 

De eerste die overweldigend bewijs voor de realiteit van het probleem van donkere materie verzamelde, was de Amerikaanse astronome Vera Rubin. Tussen 1960 en 1970 observeerde ze met haar collega Kent Ford de rotatiekrommen van tientallen sterrenstelsels. In een rotatiekromme wordt de rotatiesnelheid (v) van de sterren rond het centrum van het sterrenstelsel uitgezet tegen hun afstand (R) tot het centrum, zoals te zien is in afbeelding 2. Als je weet wat de massa van de sterren en het gas in het sterrenstelsel is, kun je de vorm van deze rotatiekromme voorspellen door middel van Newtons zwaartekrachtwetten.

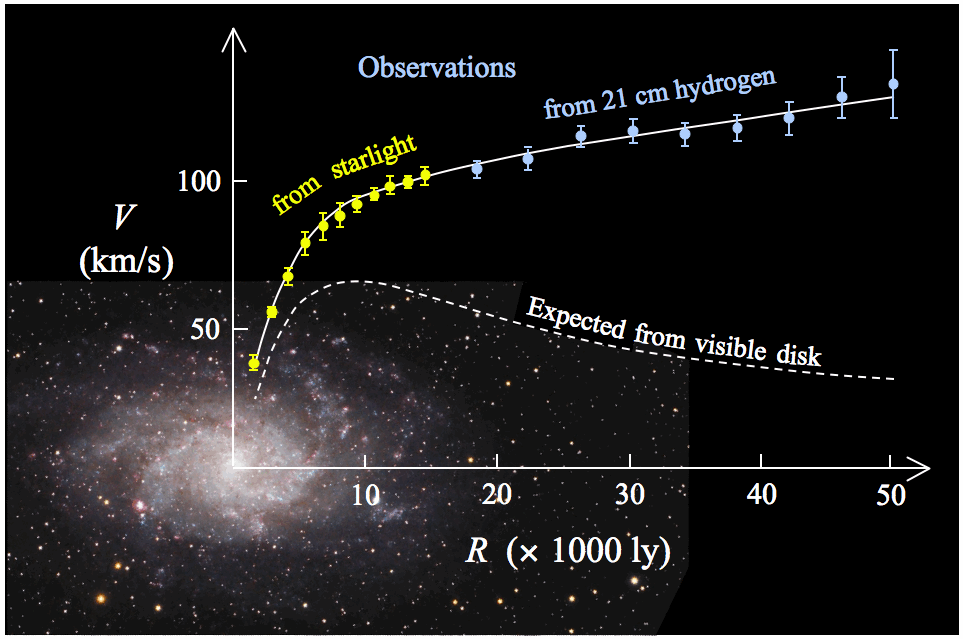
Afbeelding 2. Rotatiekromme.De rotatiekromme van een sterrenstelsel. De datapunten zijn de gemeten snelheden van sterren (geel) en gas (lichtblauw) rond het centrum van het sterrenstelsel. De onderste stippellijn is de rotatie die wordt verwacht naar aanleiding van de zichtbare materie in het sterrenstelsel. Deze komt echter totaal niet met de gemeten rotatiesnelheid overeen! (Bron: Stefania de Luca)

De centripetaalkracht (F_c) die nodig is om een roterende ster met massa (m) in zijn baan te houden,

\(F_c = \frac{m v^2}{R}\)

is namelijk gelijk aan de zwaartekracht die op massa (m) wordt uitgeoefend:

\(F_g = \frac{G M(<R) m}{R^2}\)

In deze formule is G de zwaartekrachtconstante, en M(<R) betekent alle massa die zich binnen de baan van massa (m) bevindt. Door de formule F_c = F_g op te lossen, vinden we dat de rotatiesnelheid (v) als functie van de straal (R) tot het centrum gelijk is aan:

\(v = \sqrt{\frac{G M(<R)}{R}}\)

We zien hier dat de rotatiesnelheid onafhankelijk is van de massa (m) van de ster, maar enkel afhangt van de totale massa M(<R) binnen de baan van het object, en van de straal (R) van deze baan. Zoals te zien is in afbeelding 2 hoopt de meeste zichtbare massa van een sterrenstelsel zich op in het centrum. Als we de massa binnen een bepaalde straal R beschouwen, komt er buiten het centrum dus bijna geen massa meer bij, en kunnen we M(<R) beschouwen als een constante. Buiten het lichtgevende centrum van het sterrenstelsel zou de rotatiesnelheid dus evenredig moeten zijn met √(1 / R). Deze rotatiekromme is te zien als de onderste witte stippellijn in afbeelding 2. Tot haar verbazing observeerde Vera Rubin echter dat de rotatiesnelheid (v) niet daalde met afstand (R), maar gelijk bleef of zelfs bleef stijgen! Deze waarnemingen worden in afbeelding 2 getoond als de bovenste punten, die zijn gemeten door middel van het licht van roterende sterren (geel) of gas (lichtblauw).

Het is niet verwonderlijk dat Vera’s ontdekking in eerste instantie sceptisch werd ontvangen. Haar waarnemingen bevestigden echter wel een vermoeden dat twee grootheden uit de astronomie al eerder had uitgesproken. In 1933, een jaar na het onderzoek van Oort, merkte ook de Zwitser Fritz Zwicky, tijdens zijn onderzoek naar clusters van melkwegstelsels, dat de stelsels aan de rand van het Coma-cluster te snel bewogen om door de zwaartekracht van de zichtbare materie bij elkaar gehouden te worden. Het cluster moest hiervoor zo’n 400 keer zwaarder zijn dan op grond van het zichtbare gas en de sterrenstelsels werd berekend. Frits Zwicky noemde deze missende massa zelfs ‘donkere materie’. Vera Rubin stond dus al snel niet alleen: van alle kanten bleek dat er iets niet in de haak was.

Afbeelding 3. Het Coma-clusterToen Fritz Zwicky het Coma-cluster onderzocht, ontdekte hij dat er iets vreemds aan de hand was. Volgens zijn berekeningen op basis van de snelheden van de sterrenstelsels, moest de massa van dit cluster zo’n 400 keer groter zijn dan hij uit het licht van sterrenstelsels en gas kon afleiden. (Bron: NASA / JPL-Caltech / L. Jenkins (GSFC))

Twee kosmische kampen

Voor zover we nu weten, kunnen al deze waarnemingen kortweg twee dingen betekenen:

1.  Als de totale massa van objecten veel groter is dan kan worden afgeleid uit zichtbare materie, moet er een onzichtbare massa-component zijn die ervoor zorgt dat zowel afzonderlijke sterrenstelsels als clusters zo snel kunnen roteren zonder uit elkaar te vliegen. Deze massa wordt donkere materie genoemd.
2.  De zwaartekrachtwetten van Newton en Einstein werken op de kosmische schaal niet hetzelfde als op kleine schaal, zoals op aarde en binnen ons zonnestelsel. Er moet een aanpassing op de huidige zwaartekrachttheorie komen, ook wel “geModificeerde Newtoniaanse Dynamica” (MoND) genoemd.

In beide kampen werken grote groepen astrofysici al jaren aan een definitieve verklaring van het probleem van donkere materie, maar tot de dag van vandaag is de strijd nog altijd niet beslecht. Hoe kom je er nu achter welke van deze twee opties donkere materie het beste verklaart? En als donkere materie echt materie is, waar kan het dan uit bestaan? Of zo niet, welke aanpassing moeten we aan onze zwaartekrachtwetten maken om deze met de natuur te laten kloppen? Al deze en meer vragen komen aan bod in komende artikelen van dit dossier over donkere materie. Voor nu moeten we ons maar gelukkig prijzen, dat de donkere materie er in ieder geval voor zorgt dat ons sterrenstelsel niet uit elkaar vliegt!

Bibliografie:

•  Introduction to Cosmology; Barbara Ryden; Pearson Education Inc. 2003
•  Particle Dark Matter: Evidence, Candidates and Constraints; Gianfranco Bertone, Dan Hooper, Joseph Silk
  

Het volgende artikel in dit dossier verschijnt op vrijdag 19 februari.