Afbeelding 1. Diffusie.Hoe snel verspreidt inkt zich in water? Foto: Zvonimir Loncaric.
Het probleem vereenvoudigd
De tijdstippen waarop het intktmolecuul van richting verandert, zijn eveneens grillig. We vereenvoudigen het probleem door die grilligheid eruit te halen. We nemen aan dat het molecuul alleen op tijdstippen t = 1, 2, 3, … van richting verandert. Dat is weliswaar onrealistisch, maar zo kunnen we misschien enige intuïtie ontwikkelen voor het probleem.
Om dezelfde reden vereenvoudigen we nog verder: we nemen aan dat het molecuul langs een lijn beweegt en dat het molecuul tussen opeenvolgende tijdstippen steeds dezelfde afstand aflegt. Kortom, we hebben een deeltje dat beweegt langs de getallenlijn – zie afbeelding 2 hieronder. Het start op tijdstip t = 0 in x = 0 en iedere tijdstap gaat het 1 eenheid naar rechts of naar links. Ten slotte nemen we aan dat het molecuul steeds een (zuiver) ‘muntje werpt’ om te bepalen welke kant het op gaat: kop = links en munt = rechts.
Een wiskundige oplossing
De positie x van het deeltje op tijdstip t = n (met n = 1, 2, 3, …) is een toevalsvariabele: die positie ligt niet met zekerheid vast. Op t = 2 zijn bijvoorbeeld de posities x = -2, x = 0 en x = 2 mogelijk. De kansen hierop (ga zelf na!) zijn respectievelijk 1/4, 1/2 en 1/4. De verwachtingswaarde (de gemiddelde positie) is dus
1/4 × (-2) + 1/2 × 0 + 1/4 × 2 = 0.
Op t = 3 vind je op dezelfde manier voor de gemiddelde positie
1/8 × (-3) + 3/8 × (-1) + 3/8 × 1 + 1/8 × 3 = 0.
Een opmerking tussendoor: de gemiddelde positie is dus niet de meest waarschijnlijke positie! Voor t = 3 is de kans dat het deeltje zich op x = 0 bevindt zelfs gelijk aan 0. Niets bijzonders: de verwachtingswaarde van een worp met een dobbelsteen is 7/2, maar de kans op dat exacte resultaat is ook 0.
Door de symmetrie van het probleem – er is geen voorkeur voor links of rechts – is x = 0 de gemiddelde positie voor iedere t = n. Om iets te zeggen over de afstand op t = n moeten we dus bijvoorbeeld kijken naar de absolute waarde |x| van x te kijken. Het is echter gebruikelijker om naar de gemiddelde waarde van x2 te kijken, omdat de wiskunde dan gemakkelijker is dan wanneer we |x| nemen. Laten we die gemiddelde waarde van x2 noteren als ‹x2›. Voor t = 2 vinden we
‹x2› = 1/4 × (-2)2 + 1/2 × 02 + 1/4 × 22 = 2
en voor t = 3 vinden we
‹x2› = 1/8 × (-3)2 + 3/8 × (-1)2 + 3/8 × 12 + 1/8 × 32 = 3.
Het is wiskundig niet heel lastig te bewijzen dat dit patroon zo verder gaat: voor t = n geldt ‹x2› = n.

Afbeelding 2. Een wiskundig model voor diffusie.Een animatie van het eenvoudige model voor diffusie dat hierboven is beschreven: de rode stip stelt één inktmolecuul voor.
Na n stappen verwachten we dus dat de toevalsvariabele x2 de orde van grootte n heeft. We verwachten dan ook dat x zelf orde van grootte √n heeft. Dit is de bekende wortel-n-wet uit de statistiek. Als je 1.000.000 keer met een zuivere munt gooit, dan verwacht je dat de afwijking van het gemiddelde aantal keren kop (500.000) de orde van grootte van 1000 heeft. Natuurkundig: om de straal van de inktvlek te laten verdubbelen moet je vier keer zo lang wachten.
Natuurkundige oplossingen
We kunnen het bovenstaande probleem ook met dimensie-analyse oplossen. Als voorbeeld voor deze techniek bekijken we eerst een ander probleem waarvan we de oplossing al kennen: de slinger.
De slinger
We hebben een slinger van lengte L en massa m. Die slinger beweegt onder invloed van de zwaartekracht. Wrijving negeren we. De gebruikelijke (gecompliceerde!) aanpak gaat als volgt: we ontbinden Newtonds wet F = m a in een horizontale en een verticale component, wat leidt tot een differentiaalvergelijking voor de hoek θ die de slinger maakt met de verticale richting. Die vergelijking luidt
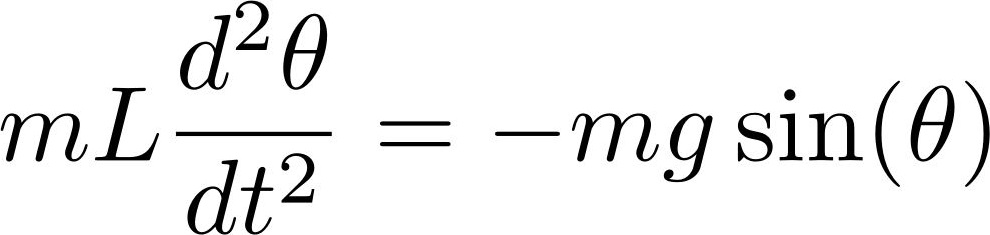
De massa valt weg:
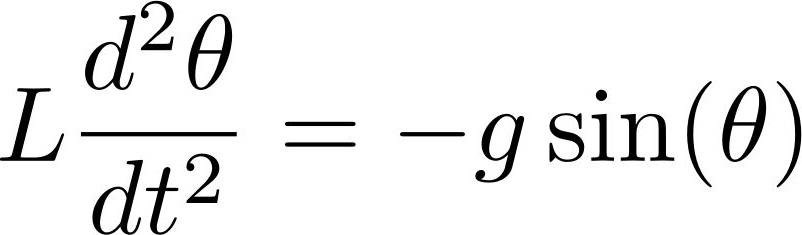
Nu nemen we aan dat de hoek θ klein is, zodat we de benadering sin(θ) ~ θ kunnen gebruiken. Oplossen van de differentiaalvergelijking leidt tot bijvoorbeeld θ(t) ~ cos(ωt) met ω = √(g / L). De periode van de trilling is dan T = 2π / ω = 2π √(L / g).
Dimensie-analyse: de slinger
We gaan nu het probleem van de trillingstijd van de slinger veel eenvoudiger oplossen: met dimensie-analyse. Het voordeel van dimensie-analyse is dat deze methode razendsnel en gemakkelijk is. Het nadeel is dat je niet altijd exacte resultaten krijgt. De redenering is als volgt. De formule voor de tijd T = … heeft aan de rechterkant als mogelijke natuurkundige ingrediënten: de massa m, de lengte L en de versnelling g van de zwaartekracht. Hun eenheden zijn respectievelijk kg, m en m/s2. Hoe kan ik daaruit een tijd bakken, die de eenheid s heeft?
In de formule voor T moet wel de constante g voorkomen, want dat is de enige parameter waarvan de eenheid secondes bevat. Sterker nog: we kunnen aan de hand van de precieze eenheid van g, m/s2, raden dat T ~ √(1/g). We zien ook dat de massa niet kan voorkomen, want we hebben geen ander ingrediënt om diens eenheid kg weer te laten wegvallen. (Vergelijk dit met de wiskundige oplossing, waar de massa ook uit het probleem wegviel.) Helaas brengt g ook de eenheid m met zich mee, dus die moeten we laten verdwijnen door een geschikte macht van L te nemen. We vinden dat L / g de eenheid s2 heeft, dus √(L / g) heeft de goede eenheid, s.
Met dimensieanalyse raden we dus dat T ~ √(L / g)! Op de wiskundige factor 2π na hebben we de goede formule geraden, zonder ingewikkelde dingen met F = m a te doen! De prijs die we moeten betalen voor onze gemakszucht is dat we de factor 2π zo niet kunnen vinden, omdat deze geen eenheid heeft.

Afbeelding 3. De slinger van Fouceault.Eén van de beroemdste typen slingers. Hoe lang de slingertijd is kun je, zonder ingewikkelde wiskunde, grotendeels bepalen met dimensie-analyse!
Dimensie-analyse: diffusie
Terug naar de uitbreidende inktvlek. Net als in het geval van de slinger kunnen we de diffusie (dat wil zeggen: het langzaam uitspreiden) van de inktvlek beschrijven met een differentiaalvergelijking. Die luidt:
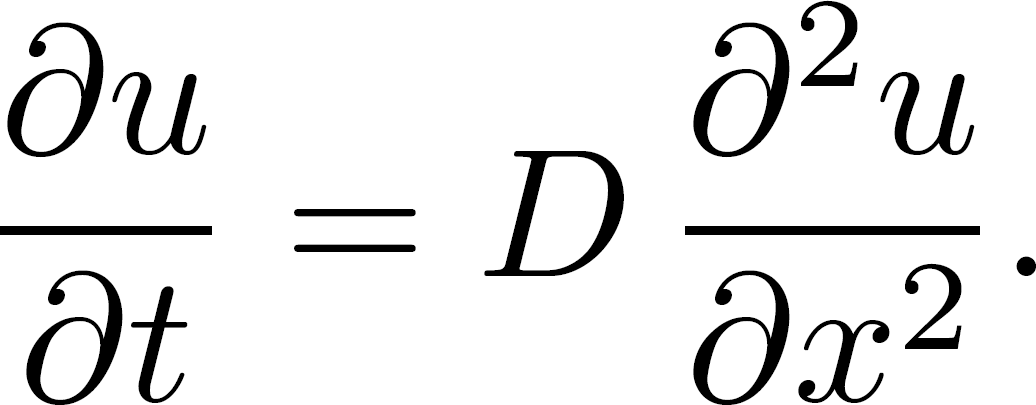
Hierbij is u = u(x,t) de concentratie van inktmoleculen op tijdstip t en plaats x. Deze functie kunnen we diff erentiëren naar t. Dit wordt genoteerd als ∂u / ∂t. De kromme ∂ geeft aan dat we ook nog naar andere variabelen kunnen differentiëren. (Preciezer: ∂u / ∂t geeft aan dat we bij het differentiëren naar t de andere variabele, x, als constante beschouwen.) Je begrijpt wat ∂2u / ∂x2 betekent: de tweede afgeleide van de concentratie u naar de variabele x, waarbij we nu juist de andere variabele t als constante beschouwen.
We gaan nu niet de differentiaalvergelijking oplossen, maar “quick and dirty” dimensie-analyse toepassen. De eenheid aan de linkerkant is c/s, waarbij ik c schrijf voor een eenheid van de concentratie u. Wat die eenheid precies is als we die uitdrukken in meer bekende eenheden hoef ik niet verder uit te werken, want deze eenheid zal snel wegvallen. De eenheid aan de rechterkant van de vergelijking is de eenheid van D maal c/m2. Om de vergelijking te laten kloppen moet de eenheid van D dus wel m2/s zijn. Uit D, de enige natuurkundige parameter die we tot onze beschikking hebben in het inktvlekverhaal, kunnen we nooit van ons leven een snelheid bakken! De inktvlek verspreidt zich dus niet met een constante snelheid: het enige wat we kunnen concluderen is dat blijkbaar de tijd evenredig is met het kwadraat van de afstand, oftewel
‹x2› ~ D × t
We hebben het wortel-n-gedrag van de inktvlek weer teruggevonden! En dat ditmaal zonder differentiaalvergelijkingen op te lossen of statistiek te bedrijven.
Dimensie-analyse: de golfvergelijking
Als contrast met de di usievergelijking bekijken we nog een andere differentiaalvergelijking: de golfvergelijking
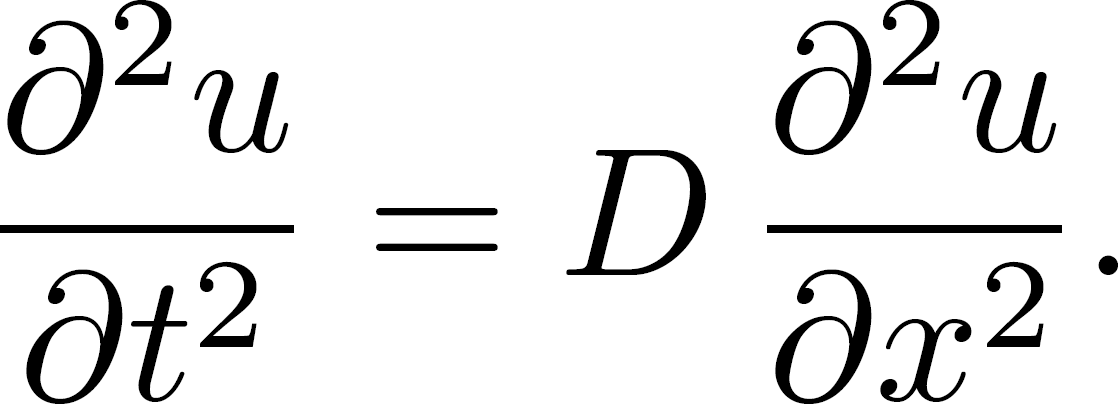
Deze vergelijking beschrijft allerlei golfverschijnselen: watergolven, geluidsgolven, lichtgolven, enzovoort. u(x,t) is nu de uitwijking van de golf op plaats x en tijdstip t. Met dimensie-analyse, net als hierboven, vinden we dat de eenheid van D nu m2/s2 is. Nu vinden we dus
‹x2› ~ D × t2
De afstand – preciezer: de root mean square distance, dus de wortel van ‹x2› – is nu dus evenredig met de tijd. Kortom, in tegenstelling tot een inktvlek beweegt een golf wél met een constante snelheid en die snelheid is evenredig met √D. Een belangrijk voorbeeld van zo’n golfverschijnsel is de Maxwell-vergelijking, die elektromagnetische straling (dus: licht) beschrijft. Het zal je nu niet meer verbazen dat √D in deze vergelijking precies de lichtsnelheid blijkt te zijn!
