
Afbeelding 1. De kilogram.Een kopie van “Le Grand K”, waarmee de waarde van een kilogram wordt bepaald. Afbeelding: Wikipedia.
Eenheden
Veel natuurkundig onderzoek draait om het bepalen van hoeveelheden en groottes. Hiervoor is het belangrijk dat we een goed gedefinieerde eenheid hebben om een hoeveelheid in uit te drukken. Het meest gebruikte systeem hiervoor is het zogeheten SI-stelsel, bestaand uit zeven basiseenheden: meter (m), kilogram (kg), seconde (s), Ampère (A), Kelvin (K), mol, en candela (Cd). (Zie hierover ons dossier over grootheden en eenheden.)
Het is noodzakelijk dat deze eenheden gedefinieerd worden op zo’n manier dat ze altijd dezelfde waarde hebben. De meter is bijvoorbeeld gedefinieerd als precies één 299.792.458e van de afstand die licht voortbeweegt in vacuüm in één seconde. In andere woorden: de definitie van een meter is afhankelijk van de snelheid van licht – een natuurconstante is die overal in het universum hetzelfde is. Een andere specifiek gedefinieerde eenheid is de seconde, gedefinieerd als precies 9.192.631.770 periodes van trilling van de elektronschil van een cesium-133 atoom.
De kilogram
Naast deze definities valt de kilogram nogal op, omdat die zo ouderwets is bepaald: in tegenstelling tot de andere eenheden in het SI-stelsel, wordt de kilogram niet bepaald door een fundamentele fysische eigenschap. Al sinds 1889 wordt de massa van een kilogram bepaald door de massa van “Le Grand K”, oftewel de internationale prototype kilogram (IPK), bewaard in het Internationaal Bureau voor Maten en Gewichten in Parijs.
Deze model-kilogram is een metalen cilinder van 39 mm hoog en 39 mm breed, een legering van 90% platina en 10% iridium. Platina is een metaal met merkwaardige weerstand tot oxideren, extreem hoge dichtheid, goede elektrische en warmte-geleidingsvermogen, en lage magnetische gevoeligheid. De toevoeging van iridium maakt het materiaal harder, wat handig is voor een object waarvan we willen dat het altijd dezelfde massa behoudt. Als extra maatregel om ervoor te zorgen dat de massa van de cilinder hetzelfde blijft, wordt de kilogram – evenals de zes kopieën ervan – bewaard in een omgevingsgecontroleerde kluis in een kelder. Landen kunnen voor hun nationale standaard een officiële kopie van de IPK krijgen, die ongeveer iedere 40 jaar met de originele in Parijs wordt vergeleken voor ijking.
Nadelen
Het probleem met zo’n fysiek object als maatstaf is dat een macroscopisch object veranderingen kan (en zal) ondergaan als gevolg van bijvoorbeeld kleine veranderingen van de omgeving waarin het wordt bewaard, waardoor de maat niet echt nauwkeurig genoeg is voor natuurkundige schalen van grootte. Neem als voorbeeld de massa van een elektron, ongeveer 9,1 × 10-31 kg; dat is dus 0,000…91 kg, met 30 nullen voor de negen! Hoewel de echte waarde van de massa van het elektron natuurlijk niet verandert, wordt de officiële numerieke waarde iedere vier jaar aangepast zodat die overeenkomt met de waarden die (steeds nauwkeuriger) gemeten worden op verschillende plekken op de wereld – elk op basis van nationale kilogram-standaarden die allemaal met een minuscule hoeveelheid verschillen. Dit is natuurlijk enorm onhandig. Hier bovenop zijn andere eenheden zoals de mol en de ampère afhankelijk van de kilogram.
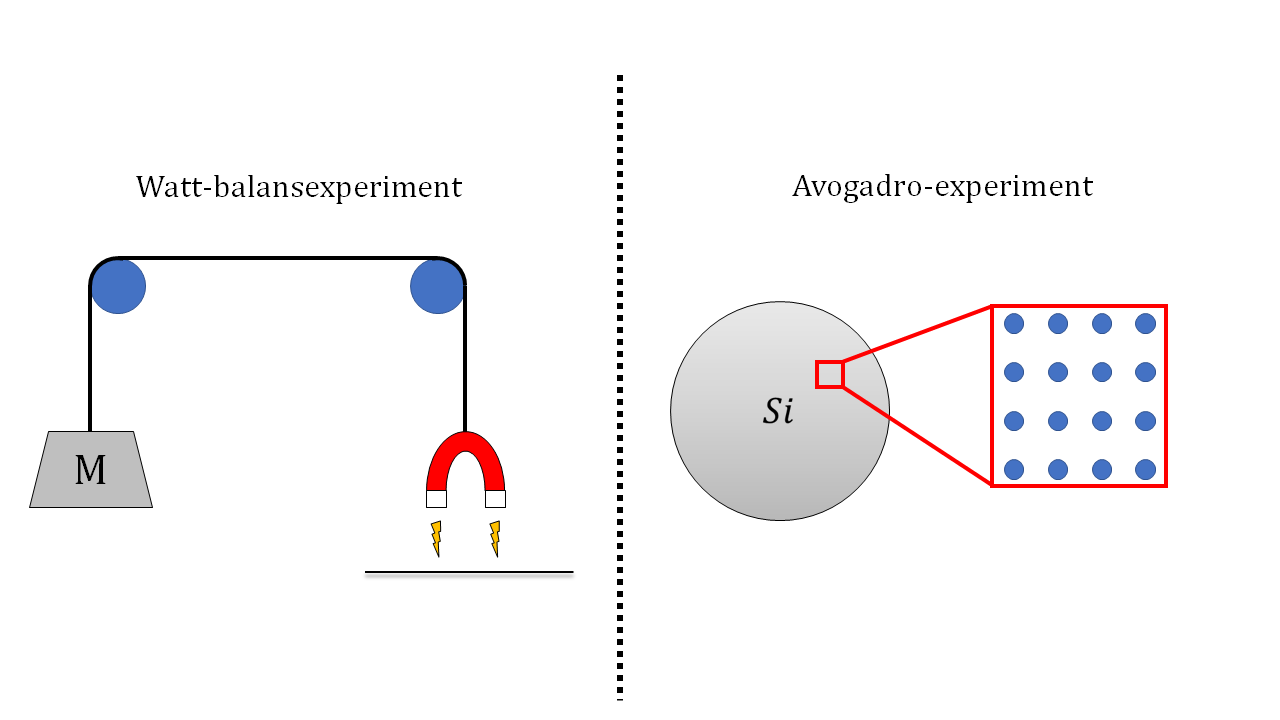
Afbeelding 2. Meten van de kilogam.Een schematische weergave van de principes achter de twee experimenten waarmee de massa van een kilogram op basis van universele natuurconstanten gedefinieerd kan worden.
Dit alles was genoeg aanleiding voor metrologen om een nieuwe standaard te bedenken die stabieler zou zijn. Hiervoor is het belangrijk dat de waarde van een kilogram bepaald wordt met behulp van een natuurconstante, net zoals de snelheid van licht gebruikt wordt om de lengte van een meter te definiëren. Er zijn twee experimenten bedacht om dit probleem op te lossen: het “Watt-balansexperiment”, en het “Avogadroexperiment” (afbeelding 2). Het eerste hiervan compenseert de zwaartekracht die een gewicht naar beneden trekt met een elektromagnetische kracht. Hierbij komen meerdere quantummechanische effecten bij kijken, die we goed kunnen beschrijven. Zo kunnen we de massa direct relateren aan de constante van Planck.
In het tweede experiment wordt een macroscopische massa gerelateerd aan de massa van een enkel atoom, en daardoor ook aan de constante van Avogadro. Om de exacte hoeveelheid atomen in een blok van materiaal te kunnen bepalen, moet het een perfect geordend (mono-)kristal zijn. Dat wil zeggen: om de hoeveelheid atomen direct te kunnen koppelen aan de totale massa, moet er maar één soort atoom in het kristal zitten, en maar één isotoop hiervan, zodat ieder atoom dezelfde massa heeft. Voor dit experiment wordt een bol van een perfect kristal van (isotopisch puur) silicium gebruikt, die geconcentreerd is in tienduizenden centrifuges! De resultaten van deze twee experimenten zijn nu nog enigszins afwijkend van elkaar, en zullen eerst met elkaar overeen moeten komen voor ze een nieuwe definitie van de kilogram kunnen bepalen.
Nieuwe kilogram?
Iedere vier jaar wordt er een bijeenkomst gehouden waarin vertegenwoordigers van alle lidstaten en geassocieerde staten van de zogeheten Meter-Conventie beslissen wat de toekomst van de standaardeenheden zal zijn, en hoe dit zal worden geïmplementeerd op een wetenschappelijk en politiek niveau. De volgende bijeenkomst is in november 2018, en dat zou als de definitie van de kilogram inderdaad wordt aangepast een van de meest belangrijke bijeenkomsten tot nu toe kunnen worden.
De voorgestelde verandering aan de definitie van de kilogram is een gevolg van een decennialang plan om alle eenheden te relateren aan natuurconstanten, zodat ze niet alleen op aarde, maar ook op Mars of zelfs in andere sterrenstelsels hun betekenis behouden. Het voorlopige plan is om het vernieuwde SI-stelsel in te voeren op 20 mei 2019, symbolisch op Wereld Metrologie Dag. Houd tegen die tijd dus het nieuws in de gaten om te zien of we inderaad een “nieuwe kilogram” krijgen!