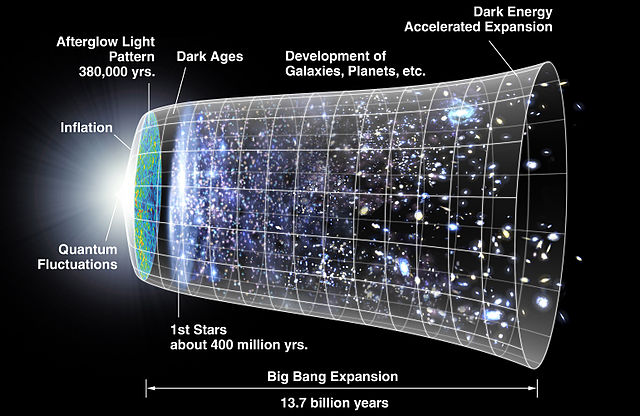
Afbeelding 1. De groei van het heelal.Vandaag de dag dijt het heelal versneld uit; een gevolg van de kosmologische constante. Maar hoe groot is de energiedichtheid die deze uitdijing veroorzaakt? Afbeelding: NASA/WMAP Science Team.
Dimensies en groottes
Een redelijk willekeurige vraag uit de theoretische natuurkunde: hoe groot is een zwart gat met dezelfde massa als de zon? Het bepalen van het antwoord op een dergelijke vraag vergt veel ingewikkeld rekenwerk, maar het schatten van het antwoord is verrassend eenvoudig. We weten namelijk dat in de fysica van zwarte gaten twee belangrijke natuurverschijnselen een rol spelen: de zwaartekracht en de snelheid van het licht. In allebei die natuurverschijnselen is een specifieke natuurconstante van belang in de zwaartekrachtswetten de zwaartekrachtsconstante van Newton,
G = 6,67 × 10-11 m3 kg-1 s-2
en voor het bewegen van het licht natuurlijk de lichtsnelheid zelf,
c = 3,00 × 108 m s-1.
In het hierboven genoemde vraagstuk komt natuurlijk ook de massa van de zon voor:
M = 1,99 × 1030 kg.
Aangezien het vraagstuk ging over de grootte van een zwart gat, zouden we nu kunnen proberen om van deze drie grootheden een combinatie, L, te maken die de eenheid “meter” heeft, en dus een grootte weergeeft. Wat spelen met de eenheden levert al snel een oplossing:
L = M G / c2 ≈ 1500 m
Dit geschatte antwoord blijkt goed in de buurt te komen van het échte antwoord: de straal van een zwart gat zo zwaar als de zon is zo’n 3 kilometer, twee keer zo veel als het eenvoudige antwoord hierboven.
Dit rekensommetje heeft een belangrijke moraal. Door alleen maar de dimensies (de eenheden) van de relevante grootheden te bekijken, kunnen we vaak in de natuurkunde al een heel goede schatting maken van de uitkomst van een probleem. Zie bijvoorbeeld dit artikel voor een aantal andere voorbeelden.
De slechtste voorspelling in de natuurkunde
De methode van dimensie-analyse die we hierboven hebben beschreven, werkt vaak heel goed. Soms leidt dit recept echter ook tot volledig onjuiste antwoorden! Het beroemdste voorbeeld daarvan is waarschijnlijk de kosmologische constante, de energiedichtheid van lege ruimte.
Dat lege ruimte überhaupt een energie heeft, is niet direct duidelijk. Het wordt misschien aannemelijker als we bedenken dat in de quantummechanica “lege ruimte” eigenlijk helemaal niet leeg is – er ontstaan en verdwijnen continu paren van deeltjes – en dat in de relativiteitstheorie ruimte ook een buigzaam “materiaal” is, wat dus best eens een energie zou kunnen hebben.
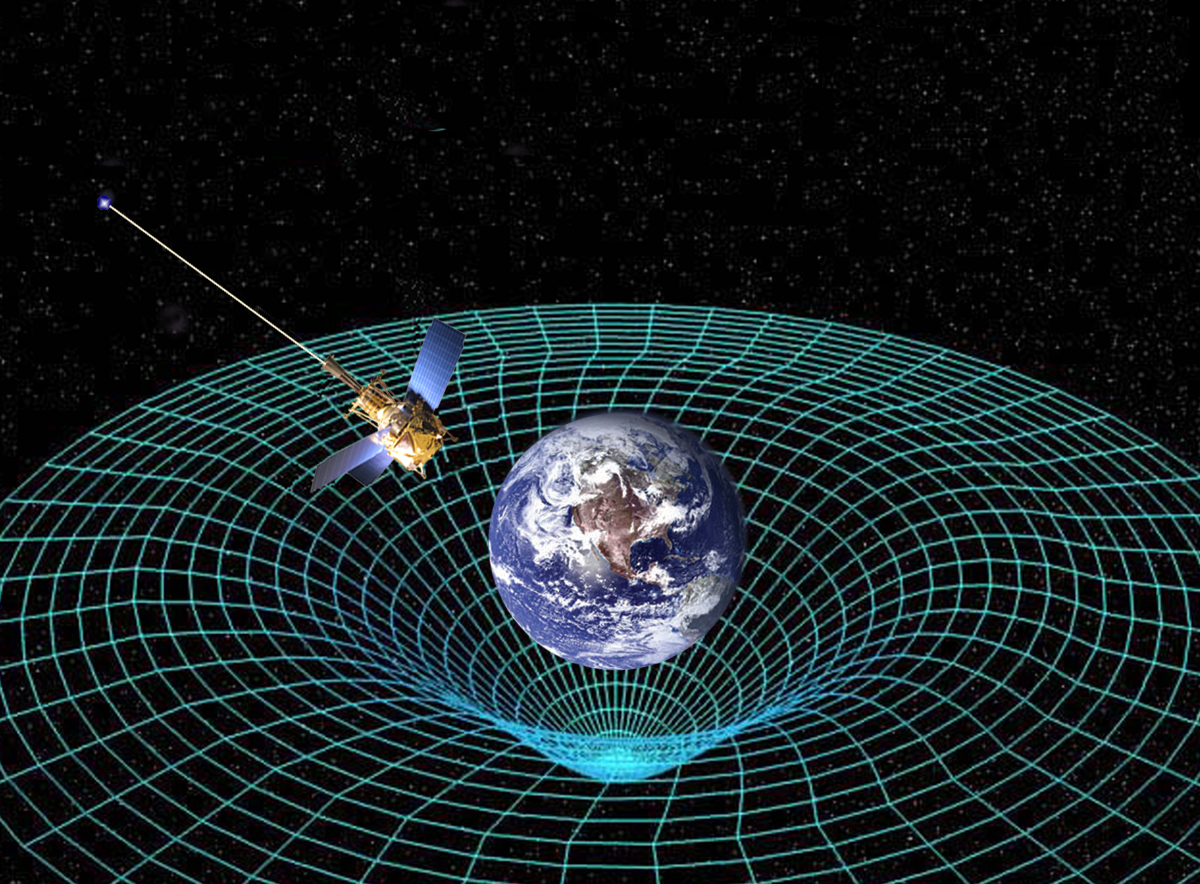
Afbeelding 2. Ruimtetijdrubber.Volgens de relativiteitstheorie is ruimte (en tijd) een “materiaal” dat vervormd kan zijn. Heeft dit materiaal net als andere materialen ook een energiedichtheid? Afbeelding: NASA.
Dat lege ruimte inderdáád een energie heeft, weten we sinds het einde van de jaren 90. Toen werd ontdekt dat alle sterrenstelsels in het heelal versneld van ons vandaag bewegen. Die versnelling wordt precies veroorzaakt door de energie van de ruimte tussen die sterrenstelsels in. Sinds de jaren 90 weten we dezelfde metingen ook hoe groot de kosmologische constante is. Maar voor we het antwoord geven: zouden we die uitkomst ook kunnen raden?
De energiedichtheid van lege ruimte kunnen we bijvoorbeeld meten in Joule per kubieke meter. De eenheid Joule kan geschreven worden als kg m2 s-2, dus om een aantal Joule per kubieke meter te bepalen moeten we een grootheid construeren die als eenheid kg m-1 s-2 heeft. Uit welke natuurconstantes moeten we deze energiedichtheid opbouwen? In het bepalen van de energie van het vacuüm spelen de relativiteitstheorie en de quantummechanica een rol, dus we zullen de natuurconstantes moeten gebruiken die in die theorieën voorkomen. Naast de al eerder genoemde zwaartekrachtsconstante G en de lichtsnelheid c is er nog één zo’n constante: de quantummechanische constante van Planck, ħ, die een waarde heeft van
ħ = 1.055 10-34 kg m2 s-1
Uit G, c en ħ, moeten we dus een dimensie-combinatie zien te maken, laten we die ρdim noemen, die onze gewenste eenheid J/m3 oftewel kg m-1 s-2 heeft. Probeer de puzzel vooral zelf op te lossen; de juiste combinatie blijkt na wat puzzelen
ρdim = c7 / ħ G2 = 4,65 × 10113 kg m-1 s-2
te zijn. Mooi, daarmee hebben we dus, net als in het voorbeeld van het zwarte gat, een voorspelling voor de gemeten waarde. Bij het zwarte gat zaten we een betrekkelijk kleine factor 2 fout. Hoe pakt dat uit bij de kosmologische constante? Zoals gezegd is de waarde daarvan in de jaren 90 gemeten; de gevonden waarde, ρvac, bleek gelijk te zijn aan
ρvac = 5,31 10-10 kg m-1 s-2.
Onze voorspelling blijkt er maar liefst 123 factoren 10 naast te zitten! De reden voor de kreet “de slechtste voorspelling uit de natuurkunde” moge duidelijk zijn.
Een verrassend argument
Om te begrijpen waarom dimensie-analyse zo’n extreem slecht resultaat geeft, zouden we natuurlijk graag een preciezere berekening doen op basis van de quantummechanica en de relativiteitstheorie waaruit wél het juiste antwoord komt, zodat we kunnen zien waar de schatting de mist in gaat. Helaas is er tot op de dag van vandaag niemand in geslaagd om zo’n berekening te doen. Dat is misschien niet heel verrassend: we weten immers niet goed hoe we quantummechanica en relativiteit tot één theorie moeten samensmelten; zelfs het juiste raamwerk voor de berekening bestaat dus nog niet! Vooralsnog blijft de extreem kleine waarde van de kosmologische constante dus een groot raadsel voor fysici – misschien wel het grootste raadsel uit de hele kosmologie.

Afbeelding 3. Steven Weinberg.Foto: Larry D. Moore (CC BY-SA 3.0).
Hoewel een precieze berekening dus niet gedaan kan worden, bestaat er wel een verrassend argument van de bekende Amerikaanse natuurkundige Steven Weinberg wat mogelijk wat licht werpt op ons raadsel. Weinbergs argument is een variant op het antropisch principe, dat zegt dat het feit dat wij de natuur kunnen waarnemen, automatisch betekent dat de natuurwetten dus zó moeten zijn dat het bestaan van intelligente waarnemers mogelijk is.
In eerste instantie klinkt dat principe nogal vreemd. Waarom zou de natuur “ervoor gekozen” hebben om intelligente waarnemers mogelijk te maken? Maar stel je bijvoorbeeld eens voor dat in allerlei verschillende heelallen, of op allerlei verschillende plekken in ons heelal, allerlei nét iets andere natuurwetten zouden gelden. In welk van al die verschillende heelallen zouden wij ons dan bevinden? Natuurlijk in elk geval in een heelal waar de natuurwetten zó zijn dat er intelligent leven mogelijk is. Bestaan al die verschillende mogelijkheden ook? Dat is allesbehalve duidelijk, maar er zijn allerlei natuurkundige modellen, zoals de snaartheorie, waarin het bestaan van een “landschap” heel veel verschillende heelalvormen in elk geval een serieuze mogelijkheid lijkt.
Goed, laten we dus eens aannemen dat er iets zit in het antropische principe. Kunnen we dan begrijpen waarom juist onze extreem kleine kosmologische constante intelligent leven mogelijk zou maken? Weinbergs antwoord: jazeker! Zoals aan het begin van dit artikel gezegd, is het namelijk de kosmologische constante die de uitdijing van het heelal drijft. Zou de kosmologische constante groter zijn, dan zou het heelal nog veel sterker versneld uitdijen. Dat effect blijkt zo extreem te zijn dat een iets grotere kosmologische constante er al toe leidt dat alle materie in het vroege heelal met zo’n grote snelheid uit elkaar zou zijn gedreven dat er nooit sterren en planeten gevormd hadden kunnen worden. Het heelal zou vooral lege ruimte geworden zijn, met hier eens een deeltje en daar eens een deeltje. Het lijkt daarmee vrijwel onmogelijk dat in een dergelijk heelal complexe, intelligente levende wezens kunnen ontstaan. Omgekeerd: zou de kosmologische constante er voor zorgen dat het heelal niet versneld maar juist vertraagd uitdijt, dan kan de waarde óók niet te groot zijn, omdat dat het heelal binnen een mum van tijd zou stoppen met uitdijen en weer in elkaar zou storten.
Weinberg kon uitrekenen hoe klein de kosmologische constante moest zijn om de vorming van sterren en planeten wél mogelijk te maken en het instorten van het heelal níet, en het antwoord bleek grofweg een factor 100 groter te zijn dan de gemeten waarde. Twee factoren tien ten opzichte van 123 factoren tien – beslist een flinke vooruitgang!

Afbeelding 4. Een goed gevuld heelal.Hoewel ons heelal natuurlijk voor een groot deel uit lege ruimte bestaat, zit de materie toch nog dicht genoeg op elkaar om sterren en sterrenstelsels te vormen. Zou het heelal té snel uitdijen, dan zouden deze processen niet meer kunnen plaatsvinden. Foto: Hubble Team.
Hoe serieus we Weinbergs argument moeten nemen is in zekere zin een kwestie van smaak; is het antropisch principe “echte natuurkunde”, of eerder een filosofische redenering? Het moge duidelijk zijn dat elke natuurkundige liever een mooie, wiskundige berekening op basis van de quantummechanica en de relativiteitstheorie zou zien, maar zolang zo’n berekening niet bestaat is het antropische argument van Weinberg misschien helemaal zo gek nog niet.