
Afbeelding 1. Een zwart gat.Afbeelding: NASA/CXC/A.Hobart.
In het eerste deel van dit tweeluik, twee weken geleden, besprak ik de informatieparadox – in het kort: zwarte gaten lijken informatie te vernietigen, in strijd met de ‘tijdsomkeerbaarheid’ van quantummechanica. In het bijzonder zagen we hoe we die paradox kunnen formuleren in termen van het begrip entropie. We zagen dat het ‘oplossen’ van de informatieparadox neerkomt op het reproduceren van de Pagekromme. In de lente van 2019 lukte het twee onafhankelijke onderzoeksgroepen om dit te doen: enerzijds de promovendus Geoffrey Penington van Stanford University, en anderzijds een groep onderzoekers uit Princeton en Santa Barbara: Ahmed Almheiri, Netta Engelhardt, Donald Marolf en Henry Maxfield. Vandaag bespreek ik hóe ze dat reproduceren van de Pagekromme hebben gedaan.
Verstrengelingsentropie en oppervlakken
Zoals we in het eerste artikel in deze serie zagen, zijn we geïnteresseerd in de situatie waarin een zwart gat ontstaat (doordat heel veel materie samengeperst wordt) en vervolgens verdampt door Hawkingstraling uit te zenden. Die straling vangen we op in een ‘bad’, en we willen weten hoe de entropie van die opgevangen straling, Srad, in de loop van de tijd verandert. Volgens de natuurkundige Don Page moet dit de naar hem vernoemde Pagekromme opleveren: Srad neemt tijdens het verdampen van het zwarte gat eerst toe, tot de Pagetijd is bereikt, een omslagpunt waarna de entropie weer afneemt tot nul. Om Srad te kunnen uitrekenen – en te zien of die grootheid inderdaad de Pagekromme volgt – moeten we ons eerst realiseren dat de entropie waar het om gaat een verstrengelingsentropie is: een entropie die hoort bij een systeem dat niet op zichzelf staat maar ‘verstrengeld’ is met een ander systeem. In ons geval is de opgevangen Hawkingstraling verstrengeld met het binnenste van het zwarte gat dat nog niet verdampt is – weet je meer over het ene systeem, dan weet je automatisch ook meer over het andere. Om het vervolg van dit artikel te begrijpen is de precieze betekenis van die verstrengeling niet zo van belang; het belangrijkste is dat we ons realiseren dat de Hawkingstraling geen op zichzelf staand systeem is, maar nauw verbonden is met de bron ervan: het verdampende zwarte gat. De verstrengelingsentropie is een maat voor de informatie in het deelsysteem van het bad met straling, ook al is dat deelsysteem verstrengeld met de rest van het systeem.
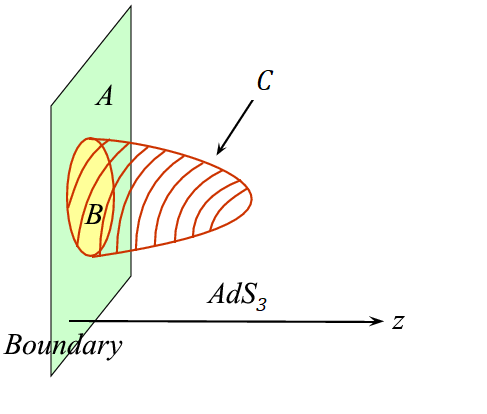
Afbeelding 2. De constructie van Ryu en Takayanagi.Het roodgearceerde oppervlak C in de driedimensionale ruimte heeft dezelfde rand als het gele gebied B in de tweedimensionale ruimte en de oppervlakte ervan is een maat voor de verstrengelingsentropie van het gebiedje B met het grotere groene gebied. (Afbeelding (bewerkt) uit ‘Holographic Entanglement Entropy: an Overview’ van Ryu, Takayanagi en Tatsuma Nishioka.)
Het uitrekenen van verstrengelingsentropie is iets waar theoretisch natuurkundigen vandaag de dag erg goed in zijn. Dat komt met name door de AdS/CFT-correspondentie, een dualiteit tussen een theorie van quantummechanica en zwaartekracht enerzijds en een theorie zonder zwaartekracht anderzijds, in één dimensie minder. In het vorige artikel zagen we al dat zwarte gaten bij uitstek objecten zijn die beschreven worden door quantumzwaartekracht – en dat blijkt met name uit de uitdrukking voor hun entropie, waarin zowel de fundamentele constante uit de zwaartekracht (G, de Newtonconstante) als die uit de quantummechanica (h, de Planckconstante) voorkomt. Die entropie is bovendien evenredig met de oppervlakte van het zwarte gat – een grootheid die inderdaad één (ruimtelijke) dimensie minder heeft! Om precies te zijn: het oppervlak van een zwart gat in een vierdimensionale ruimtetijd, dus met drie ruimtedimensies, is tweedimensionaal.
Deze regel blijkt veel breder te gelden binnen de AdS/CFT-correspondentie. Het recept is als volgt: we kunnen de tweedimensionale theorie vaak zien als een beschrijving van de “rand” van de ruimte waarin de driedimensionale theorie is gedefinieerd. Als we nu de entropie willen weten van een gebiedje B in de tweedimensionale ruimte, dan moeten we in de bijbehorende driedimensionale ruimte zoeken naar andere oppervlakken C die dezelfde rand hebben als B, maar zó dat de oppervlakte van C zo klein mogelijk is. Zie afbeelding 2 voor een schets – het rood gearceerde oppervlak stelt daar het minimale oppervlak C voor. (In de afbeelding zijn er natuurlijk kleinere oppervlakken met dezelfde rand als C, maar dat is een mankement van het tekenen in een “vlakke” ruimte; in de daadwerkelijke gekromde anti-de Sitterruimte zal het minimale oppervlak wel degelijk “naar binnen hangen”, net als in deze afbeelding.) De grootte van het minimale oppervlak, gemeten in de juiste eenheden, blijkt nu exact gelijk te zijn aan de verstrengelingsentropie in ons oorspronkelijke gebiedje B! Dit resultaat, dat in 2006 werd ontdekt door de Japanse natuurkundigen Shinsei Ryu en Tadashi Takayanagi, was een belangrijke doorbraak en wordt in de moderne theoretische natuurkunde veel gebruikt bij het bestuderen van de AdS/CFT-correspondentie in het algemeen en zwarte gaten in het bijzonder.
Gegeneraliseerde entropie en quantum-extremale oppervlakken
Hoe kunnen we het idee van Ryu en Takayanagi nu gebruiken om de verstrengelingsentropie van ons bad van straling uit te rekenen? Penington, en ook Almheiri, Engelhardt, Marolf en Maxfield, bedachten dat het handig was om te kijken naar een zwart gat in een anti-de Sitterruimtetijd. In tegenstelling tot de ruimte waarin we zelf leven (die een andere kromming heeft en ook wel “de Sitterruimtetijd” wordt genoemd) heeft zo’n anti-de Sitterruimte een rand, die dus één dimensie minder heeft: precies het soort setting waar het recept van Ryu en Takayanagi voor bedoeld is. De truc die de onderzoekers gebruikten is om ons nu voor te stellen dat die rand alle Hawkingstraling absorbeert: de rand is het bad!
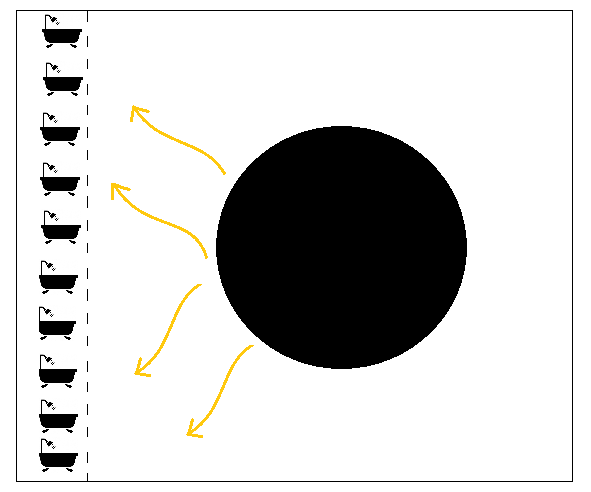
Afbeelding 3. Zwart gat, ruimte en bad.Een schematische voorstelling van de situatie: een zwart gat in een ruimtetijd met een rand, die alle straling absorbeert en daarmee fungeert als een ‘bad’.
Voor we het recept voor verstrengelingsentropie direct kunnen toepassen, hebben we nog twee ingrediënten nodig. Ten eerste moeten we ons realiseren dat we nu niet geïnteresseerd zijn in de verstrengelingsentropie van een stukje van de rand (zoals het oppervlak B in afbeelding 2), maar naar de verstrengelingsentropie van de hele rand: dat is immers het bad van straling. Dit betekent dat we ook voor het oppervlak C op zoek zijn naar een oppervlak dat zelf geen rand heeft! Oppervlakken die hieraan voldoen zijn bijvoorbeeld bollen. Ten tweede zagen we in het vorige artikel al dat we, als we een situatie bestuderen waarbij zwarte gaten betrokken zijn, naar de gegeneraliseerde entropie Sgen moeten kijken: de som van de entropie van het aanwezige zwarte gat én de overige entropie in het systeem. In dit geval moeten we iets soortgelijks doen als we de verstrengelingsentropie van ons bad van straling willen vinden. In plaats van een zo klein mogelijk oppervlak te zoeken dat dezelfde rand heeft als ons bad (zelf de hele rand van de ruimte), zoeken we naar een oppervlak O dat weliswaar dezelfde “lege” rand heeft, maar waarop de gegeneraliseerde entropie zo laag mogelijk is.
Die gegeneraliseerde entropie is in dit geval de som van de entropie die bepaald wordt door het oppervlak en de entropie van alle materie die aanwezig is tussen dat oppervlak en de rand. Voor die eerste entropie kwamen we in het vorige artikel de formule al tegen; de formule voor de totale entropie wordt dan dus:
![]()
Hierin is A(C) de oppervlakte (area) van het oppervlak C. Het recept is dus om deze twee bijdragen bij elkaar op te tellen, en vervolgens te zoeken naar een oppervlak waarvoor deze som minimaal is. Dit geeft ons het zogeheten quantum-extremale oppervlak (QES, met ‘S’ voor surface), en de daarmee uitgerekende entropie Sgen is de gezochte verstrengelingsentropie van onze straling. Het quantum-extremale oppervlak is zoals gezegd niet noodzakelijkerwijs het kleinst mogelijke oppervlak, omdat het misschien wel meer materie bevat dan een iets groter oppervlak: als de eerste term klein is, hoeft de tweede dat niet te zijn, en andersom.
Een ‘sprong’ van het QES: de Pagekromme
Wat de twee onderzoeksgroepen lieten zien, is dat er twee oppervlakken zijn die de rol van C kunnen spelen en die aan de eisen voldoen, maar die het op verschillende tijdstippen ‘winnen’ in de bepaling van de entropie. Aangezien we het over gekromde ruimtes hebben zijn deze oppervlakken moeilijk te tekenen; daarom zal ik ze alleen beschrijven. Eén van de twee oppervlakken (dit oppervlak noemen we a) heeft een heel erg kleine oppervlakte (het is een heel klein bolletje), maar tussen het oppervlak a en de rand van de ruimtetijd bevindt zich wel alle opgevangen straling. In de formule voor Sgen is de eerste term daarom verwaarloosbaar klein:
![]()
Aangezien steeds meer straling wordt opgevangen door het bad, begint deze term heel klein en groeit die in de loop van de tijd t. Het andere oppervlak (b) bevindt zich vlak binnen de horizon van het zwarte gat en omvat het grootste deel van het binnenste van het zwarte gat (omdat het zwarte gat bolvormig is, is dit wederom een oppervlak zonder rand, net als het bad). Dit oppervlak heeft dus een oppervlakte die op elk tijdstip t vergelijkbaar is met de oppervlakte van het zwarte gat, Ahor(t). Tussen dit oppervlak b en de rand van de ruimtetijd bevindt zich bijna geen materie, zodat nu juist Smaterie verwaarloosbaar klein is:
![]()
Het oppervlak van het zwarte gat krimpt naarmate het verdampt, zodat dit keer Ahor(t) een afnemende functie is van de tijd. Het mooie is nu dat Sgen(a) eerst het kleinste is (er is immers in het begin nog weinig straling opgevangen), en dus is a aan het begin van het verdampingsproces het quantum-extremale oppervlak. Dit blijft zo totdat het zwarte gat voor de helft verdampt is: dan is de oppervlakte Ahor(t) kleiner geworden, en Smaterie(t) juist groter, zodat nu Sgen(b) kleiner is dan Sgen(a): nu is b het quantum-extremale oppervlak. Wat de onderzoekers lieten zien, is dat het tijdstip waarop het QES verspringt van a naar b, precies de Pagetijd is. Daarmee reproduceerden ze de Pagekromme: de verstrengelingsentropie van de straling neemt eerst toe, en na de Pagetijd juist af. Dit is de eerste keer dat het natuurkundigen gelukt is een dergelijke berekening te doen, en het is een zeer intrigerend resultaat.
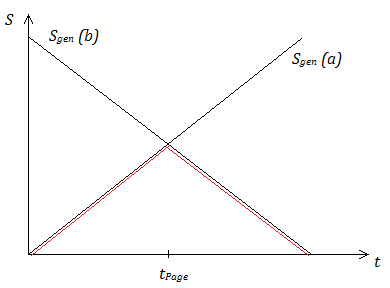
Afbeelding 4. De gevonden Pagekromme.Sgen(a) neemt toe, terwijl Sgen(b) afneemt. Het punt waarop de twee lijnen elkaar kruisen is de Pagetijd: hier verspringt het QES van oppervlak a naar oppervlak b. De Pagekromme is het rode deel van de grafiek.
Sinds de oorspronkelijke artikelen van Penington en Almheiri et al. is de discussie rondom de informatieparadox dan ook weer flink opgelaaid: er verschijnen vrijwel elke week nieuwe artikelen van gerenommeerde natuurkundigen op de preprintwebsite arxiv.org die het voorstel aanvullen, verbeteren of tegenspreken. Hoewel de berekening die ik hierboven heb uitgelegd correct lijkt, is het namelijk helaas nog niet zeker of we die ook inderdaad kunnen interpreteren als een bevredigende oplossing van de informatieparadox. Kunnen we nu ook echt begrijpen waar de informatie uit het zwarte gat blijft? En hebben we wel toegang tot die informatie? Werkt ditzelfde recept ook in ons eigen heelal, dus niet alleen in een anti-de Sitterruimte? De hele discussie hier weergeven voert te ver – en die is bovendien ook nog lang niet afgelopen. Opgelost is de informatieparadox dus nog niet, maar er zijn wel belangrijke stappen gezet. We zullen zien wat de komende maanden voor ons in petto hebben, en komen ongetwijfeld nog eens op dit onderwerp terug!