
Afbeelding 1. Een zwart gat.Een zwart gat slokt alles in zijn omgeving op. Maar wat gebeurt er met de informatie over die verdwenen materie? Afbeelding: NASA/CXC/A.Hobart.
Stel dat je een dagboek vol geheimen wil vernietigen. De meest voor de hand liggende methode is wellicht om je dagboek te verbranden – maar wat nu als je tegenstander zeer machtig, intelligent en ijverig is? In principe kan jouw vijand alle as verzamelen, samenvoegen en het dagboek reconstrueren: verbranding is een omkeerbaar proces waarbij de informatie in jouw dagboek niet verloren gaat. In theorie zou dit proces zelfs spontaan kunnen gebeuren: dat is weliswaar zeer onwaarschijnlijk, maar niet onmogelijk (zie daarvoor ons eerdere artikel over ‘de pijl van de tijd’). Deze ‘tijdsomkeerbaarheid’ geldt voor alle tot nu toe bekende natuurwetten, van relativiteitstheorie tot quantummechanica.
Je wil echter zeker weten dat je geheimen vernietigd zullen worden, en besluit daarom je dagboek in een zwart gat te gooien. Van zwarte gaten weet je namelijk het volgende: alles wordt erin opgeslokt, en hoewel ze wel verdampen (via zogeheten Hawkingstraling), valt daaruit niet af te leiden wát je precies in het zwarte gat hebt gegooid. Om preciezer te zijn: zwarte gaten zijn zogeheten zwarte stralers, objecten waarvan de uitgezonden straling alleen afhangt van hun temperatuur. In het geval van zwarte gaten is die temperatuur alleen afhankelijk van de massa ervan. Zoals we in ons dossier over zwarte gaten ook al uitlegden maakt het dus niet uit of je een dagboek van 500 gram in het zwarte gat gooit of een halve kilo kaas: als we het hele zwarte gat laten verdampen en de straling opvangen is die precies hetzelfde.
Misschien ben je nu prima tevreden: jouw geheimen zijn immers veilig. Theoretisch natuurkundigen breken zich hier echter al jarenlang het hoofd over. De theorie over straling van zwarte gaten is namelijk gebaseerd op de relativiteitstheorie en de quantummechanica, die, zoals we eerder zagen, beiden voldoen aan ‘tijdsomkeerbaarheid’ (met een mooi woord: unitariteit). Er zou dus eigenlijk helemaal geen informatie verloren mogen gaan bij dit proces! Deze schijnbare tegenspraak wordt de ‘informatieparadox’ genoemd.
Holografie als ‘oplossing’?
De paradox was zo verwarrend dat drie beroemde theoretisch natuurkundigen er in 1997 een weddenschap over afsloten: Stephen Hawking, Kip Thorne en John Preskill. Hawking en Thorne dachten dat een volledige theorie van quantumzwaartekracht uiteindelijk zou aantonen dat een zwart gat informatie kan vernietigen, terwijl Preskill van mening was dat onze bestaande theorieën kloppen, en dat Hawkingstraling tóch informatie moet bevatten. In 2004 werd de weddenschap deels beslecht: naar aanleiding van de door Juan Maldacena ontdekte AdS/CFT-correspondentie raakte Hawking ervan overtuigd dat Preskill gelijk heeft, en dat zwarte gaten geen informatie vernietigen. Hoe dat precies in z’n werk gaat, beschreven we eerder al in dit artikel.
Hoewel de meeste natuurkundigen inmiddels inderdaad denken dat zwarte gaten informatie niet vernietigen, is het nog onduidelijk hoe dat dan in z’n werk gaat. Er zijn in de loop der jaren verschillende voorstellen gedaan, waarvan we bijvoorbeeld het idee van complementariteit bespraken, en de kritiek daarop, die vaak onder de noemer van de firewall-paradox gebracht wordt. Een bevredigende oplossing kwam er niet, en de informatieparadox bleef de gemoederen van de natuurkundigen bezighouden. In de lente van 2019 werd een nieuw, veelbelovend voorstel geïntroduceerd, door twee onafhankelijke onderzoeksgroepen: enerzijds de promovendus Geoffrey Penington van Stanford University, en anderzijds een groep van onderzoekers uit Princeton en Santa Barbara: Ahmed Almheiri, Netta Engelhardt, Donald Marolf en Henry Maxfield. (Almheiri en Marolf waren overigens ook betrokken bij het formuleren van de firewall-paradox.)

Afbeelding 2. Preskill, Thorne en Hawking.John Preskill, Kip Thorne en Stephen Hawking (van links naar rechts) sloten een wereldberoemde weddenschap af over de informatieparadox. De inzet was een encyclopedie naar keuze. Foto: Caltech / Heidi Aspaturian.
Informatie en de entropie van zwarte gaten
Om de nieuwe oplossing te begrijpen, moeten we eerst een aantal andere begrippen introduceren. Allereerst moeten we begrijpen hoe we de informatieparadox kunnen formuleren in termen van de entropie van zwarte gaten. Entropie wordt over het algemeen geïnterpreteerd als een maat voor de willekeur in een natuurkundig systeem. De tweede wet van de thermodynamica stelt dat entropie (S) altijd toeneemt. Het verschil in entropie tussen een begin- en eindsituatie (ΔS) is dus altijd groter dan of gelijk aan nul:
![]()
We kunnen natuurlijk een systeem, bijvoorbeeld een ballenbak, ordenen en zo de entropie van de ballenbak laten afnemen. De tweede wet van de thermodynamica is daarmee niet geschonden: die gaat over de totale entropie van het hele universum, en terwijl jij de ballenbak ordent neemt de entropie in jou en jouw omgeving toe. Stel je nu echter eens voor dat we een object met een bepaalde (misschien zelfs heel grote) entropie in een zwart gat laten vallen – bijvoorbeeld een kop hete thee. Zodra de kop thee achter de horizon van het zwarte gat is verdwenen, kunnen we die niet meer waarnemen; het lijkt erop dat er nu echt entropie uit ons waarneembare universum verdwenen is! Deze schending van de thermodynamica-wetten kunnen we verhelpen door aan te nemen dat zwarte gaten zelf ook een entropie hebben, die toeneemt zodra het zwarte gat iets opslokt en groeit. In de context van zwarte gaten spreken we daarom over de gegeneraliseerde tweede wet van de thermodynamica:
![]()
Hierin is SBH de entropie van het zwarte gat: de zogeheten Bekenstein-Hawkingentropie. Die entropie blijkt evenredig te zijn met de oppervlakte van het zwarte gat: die oppervlakte neemt inderdaad toe als we massa toevoegen aan het zwarte gat – het zwarte gat groeit dan immers. De formule voor SBH is een van de mooiste in de theoretische natuurkunde, omdat alle fundamentele natuurkunde-constanten erin voorkomen:
![]()
Hierin is A de oppervlakte (area) van (de horizon van) het zwarte gat, k de Boltzmannconstante, c de lichtsnelheid, h de constante van Planck, en G de constante van Newton. In deze formule komen dus de thermodynamica, speciale relativiteitstheorie, de quantummechanica én de algemene relativiteitstheorie samen: een van de redenen waarom het begrijpen van zwarte gaten cruciaal is bij het ontwikkelen van een theorie van de quantumzwaartekracht.
Na dit korte uitstapje kunnen we terug naar de informatieparadox. Het begrip entropie kunnen we namelijk niet alleen thermodynamisch interpreteren; een andere veelgebruikte interpretatie is die van een entropie van onwetendheid. Als we weinig over een systeem weten, dan is de entropie hoog (het systeem is zeer ongeordend); als we juist veel kennis hebben over de toestand, dan is de entropie laag. De entropie van een systeem is dus ook een maat voor de hoeveelheid informatie die er over het systeem bekend is. Bij zwarte gaten is deze interpretatie voor de hand liggend: hoe groter het zwarte gat is, hoe groter onze onwetendheid over wat zich achter de horizon bevindt, en dus hoe hoger de entropie. We herkennen wederom de evenredigheid met het oppervlak van de horizon.
Stel nu dat we een heleboel massa verzamelen (dagboeken, hompen kaas, sterren) en samenpersen tot er een zwart gat ontstaat. Vervolgens laten we dat zwarte gat verdampen, en we vangen alle Hawkingstraling op in een ‘bad’. We kunnen nu onderscheid maken tussen de entropie van het zwarte gat (SBH) en de entropie van de straling (Srad; ‘rad’ staat voor radiation). Laten we die laatste entropie eens onder de loep nemen. Vlak voor de verdamping begint hebben we nog geen straling opgevangen, dus Srad = 0: we weten precies wat er in ons bad van straling zit (niets). Naarmate we meer straling verzamelen, groeit de entropie Srad: onze onwetendheid van wat er precies in het bad zit neemt toe – we weten niet of de opgevangen straling komt van een ster, een stukje kaas, of allebei.
Tegen de tijd dat we álle straling verzameld hebben, weten we in principe echter precies wat we in ons bad hebben zitten: alle massa die we in eerste instantie verzameld hadden! Onze onwetendheid is weer afgenomen naar nul. Ergens moet er dus een punt geweest zijn waar de entropie van de straling niet meer groeide, maar afnam. De grafiek die dit toenemen en afnemen weergeeft staat bekend als de Page-kromme, naar de theoretische natuurkundige Don Page die dit idee in 1993 introduceerde. Hij rekende uit dat het omslagpunt, dat de Page-tijd genoemd wordt, moet liggen op het moment dat de helft van het zwarte gat is verdampt. Overigens lijkt het misschien alsof het uiteindelijk weer afnemen van de entropie de (gegeneraliseerde) tweede wet schendt, maar dat is gelukkig niet het geval: we kijken hier alleen naar de entropie van de straling, niet de totale entropie.
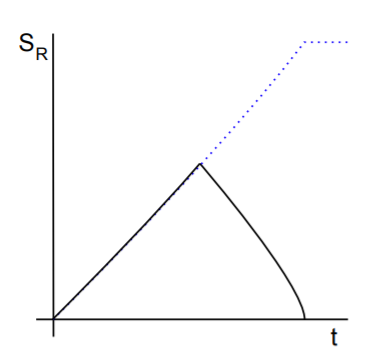
Afbeelding 3. De Page-kromme.De stippellijn is de situatie waarin informatie wél verloren gaat. Bron: Jerusalem Lectures on Black Holes and Quantum Information, Daniel Harlow – https://arxiv.org/pdf/1409.1231.pdf.
De Page-kromme is in feite een herformulering van het idee dat informatie niet verloren kan gaan. Na verdamping hebben we immers alle informatie over wat er in het zwarte gat gegooid is in ons bad van straling zitten. (Hoe we die informatie precies kunnen aflezen, is een heel andere vraag – gemakkelijk zal dat zeker niet zijn!) Als informatie wél verloren zou gaan, zou de entropie van de straling, in tegenstelling tot wat in de Page-kromme gebeurt, voor altijd toenemen. Het ‘oplossen’ van de informatieparadox komt daarmee neer op het meten van de entropie van de opgevangen Hawkingstraling en het kunnen reproduceren van de Page-kromme – en dat is precies wat de twee onderzoeksgroepen afgelopen lente gedaan hebben. Hoe ze dat precies deden is een verhaal op zich – dat verhaal lees je over een week in deel 2 van dit artikel.