
De wet van Hubble
Over de wet van Hubble is op de QU-website al eens eerder het een en ander verschenen, maar wat is die wet ook alweer? Edwin Hubble mat in 1929 de afstand tot verschillende sterrenstelsels en de snelheid waarmee ze naar ons toe of van ons af bewegen. Hij ontdekte dat vrijwel al die sterrenstelsels van ons af bewogen, en wel met een snelheid die rechtevenredig is met de afstand tot dat sterrenstelsel:
\( v = H_0 d \).
In deze formule, die tegenwoordig bekendstaat als de wet van Hubble, is \(v\) de snelheid waarmee het sterrenstelsel van ons af beweegt, \(d\) de afstand tot dat sterrenstelsel en de verhouding tussen die twee, \(H_0\), wordt de Hubbleconstante genoemd. Hoewel de data waarop Hubble zijn oorspronkelijke conclusie baseerde nog ruimte voor interpretatie openlieten, is de juistheid van zijn wet in de loop van de decennia overtuigend aangetoond.
Hoewel de wet van Hubble misschien anders doet vermoeden, betekent het feit dat alles van ons af beweegt niet dat de aarde, of de zon, of de Melkweg, het middelpunt van het universum is. Volgens de algemene relativiteitstheorie van Albert Einstein kan het zo zijn dat de ruimte uitdijt. Dit proces wordt vaak vergeleken met een rijzend krentenbrood. Terwijl het brood rijst, lijkt het vanuit elke krent gezien alsof alle andere krenten ervanaf bewegen. Dit betekent niet dat die ene krent waarvanuit we dit verschijnsel bekijken het middelpunt van het brood is, maar dat overal het brood tussen de krenten uitzet – en net zoiets gebeurt in ons heelal.
De mogelijke uitdijing van het heelal is ontdekt door Alexander Friedman en Georges Lemaître. Door aan te nemen dat het heelal homogeen en isotroop is, wat respectievelijk betekent dat het heelal er overal en in elke richting hetzelfde uitziet, kun je concluderen dat het universum óf moet uitdijen, óf samentrekken. De snelheid waarmee dat gebeurt hangt af van de dichtheid van materie, van straling en van donkere energie. In een uitdijend universum neemt de dichtheid van materie af met een andere snelheid dan de energiedichtheid van straling. Donkere energie daarentegen is een constante en de dichtheid ervan verandert niet als de ruimte uitdijt. Dit alles betekent dat de snelheid waarmee de uitdijing (of samentrekking) plaatsvindt, verandert naarmate de tijd vordert en afhankelijk is van de precieze samenstelling van de energiedichtheid. De Hubbleconstante is dus eigenlijk geen constante, maar een tijdsafhankelijke waarde. Toch wordt de parameter vaak nog steeds de Hubbleconstante genoemd, want in onze levenstijd verandert de waarde van de Hubbleparameter heel weinig.
Er zijn grofweg twee manieren om de Hubbleconstante te bepalen. De eerste methode is de ‘theoriemanier’. Vanuit de kosmische achtergrondstraling, een soort babyfoto van ons heelal, kan met het huidige kosmologische model worden doorberekend wat de Hubbleconstante nu zou moeten zijn. Volgens die berekening zou de Hubbleconstante nu 67,3 kilometer per seconde per megaparsec zijn, met een foutmarge van 1,1 kilometer per seconde per megaparsec. Dit betekent dat voor elke 3,26 miljoen lichtjaar (een megaparsec) dat een sterrenstelsel verder van ons af staat, het met 67,3 kilometer per seconde meer van ons afbeweegt.
De kosmische afstandsladder
De tweede manier om de Hubbleconstante te bepalen is de manier van Hubble zelf: door de snelheid van de sterrenstelsels die wij zien te meten en te vergelijken met de afstand tot ons. De metingen van de afstanden tot verschillende sterrenstelsels worden gedaan met behulp van de kosmische afstandsladder. Verschillende methodes werken daarbij voor sterrenstelsels op verschillende afstanden. Samen zorgen deze methodes voor de verschillende sporten van de afstandsladder, waarbij hogere sporten berusten op de lagere treden voor kalibratie.
Zo wordt voor objecten die dichtbij staan vaak een methode gebruikt die parallax wordt genoemd. Als een verre planeet – waarvan we voor het gemak even aannemen dat die stilstaat ten opzichte van de zon – in de zomer en in de winter wordt geobserveerd, zal de planeet, omdat de aarde in dat halve jaar wél beweegt, zijn verschoven ten opzichte van sterren die heel veel verder weg staan. Aan de hand van deze verschuiving kan de afstand tot de planeet worden berekend. Voor objecten die zelf ook heel ver weg staan wordt dit effect te klein en zijn dus andere methoden nodig.
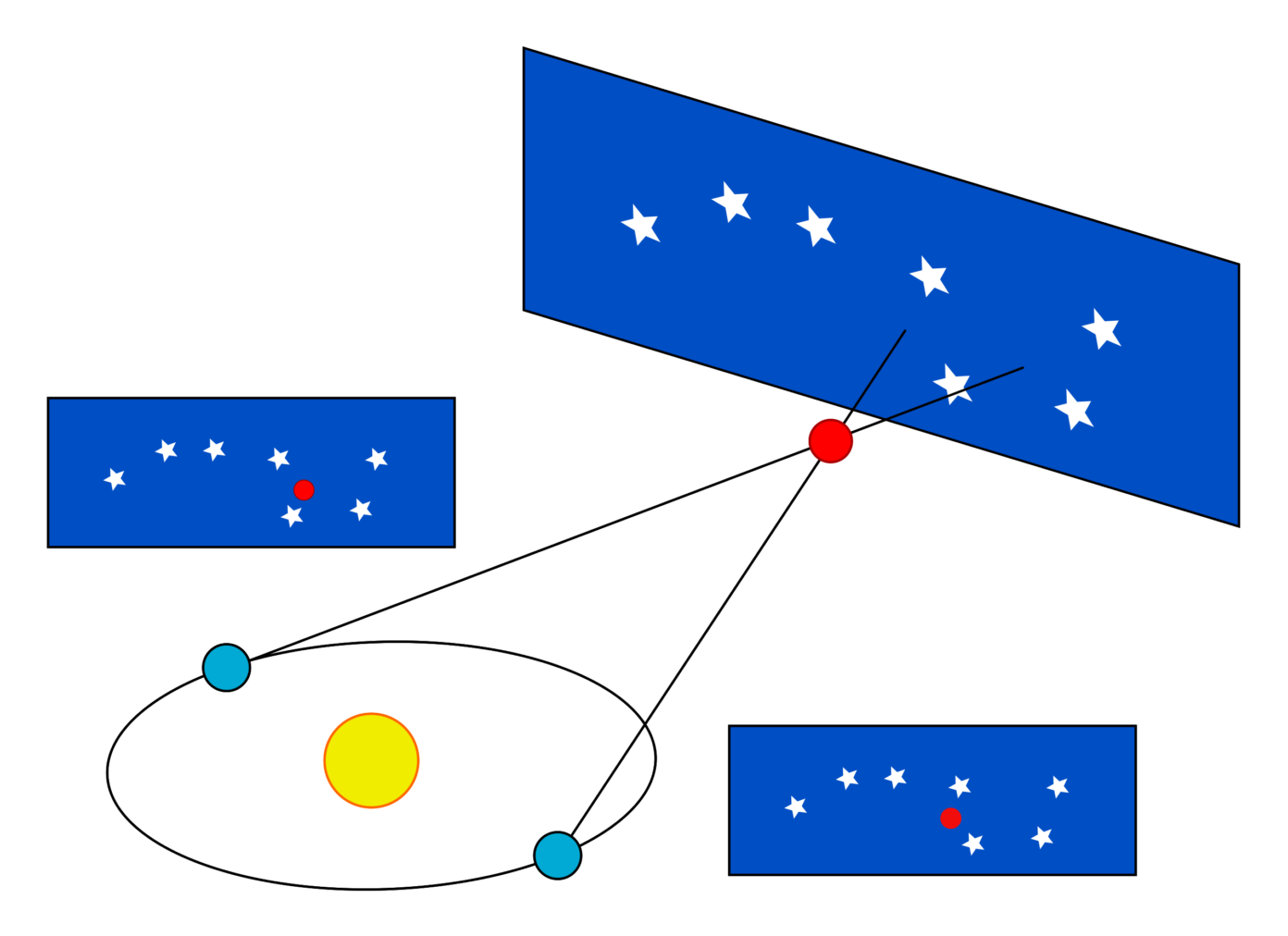
Eén zo’n andere methode is die van standaardkaarsen. Dit zijn objecten waarvan de absolute helderheid bekend is, zoals van supernovae van het type Ia of bepaalde sterren die Cepheïden worden genoemd. Doordat hun absolute helderheid bekend is, kan door de waargenomen helderheid de afstand tot die objecten worden bepaald. De helderheid van deze sterren moet natuurlijk ook zelf berekend worden: dat kan bijvoorbeeld dan weer door van Cepheïden die dichtbij staan de parallax te observeren.
Er wordt op deze manier al duidelijk hoe bepaalde sporten van de afstandsladder op elkaar bouwen. Het nieuwe onderzoek werd uitgevoerd onder leiding van Dan Scolnic, een professor aan de Duke-Universiteit in Durham. Het team van Scolnic gebruikte een ladder ontwikkeld door een ander team aan de hand van data van DESI (Dark Energy Spectroscopic Instrument). Het team ontdekte dat de onderste sport van die ladder nauwkeuriger kon worden gemaakt door een precieze afstand tot de zogeheten Coma-cluster – een betrekkelijk dichtbije groep van sterrenstelsels – toe te voegen. De afstand tot deze cluster was al wel vaker gemeten, maar de nieuwe meting was een stuk nauwkeuriger en daardoor beter te gebruiken in de afstandsladder.
Met deze methode kwam het team uit op een Hubbleconstante van zo’n 76,5 kilometer per seconde per megaparsec. Ook andere onderzoeken naar de Hubbleconstante komen significant hoger uit dan de eerdergenoemde 67,3 km/s/Mpc: vaak liggen de metingen van de Hubbleconstante door middel van de afstandsladder uit rond de 73 km/s/Mpc. Deze discrepantie tussen metingen met een afstandsladder en berekeningen uit de achtergrondstraling wordt de Hubblespanning genoemd.
De Hubblespanning
De vraag is nu dus waar deze spanning vandaan komt. Onze kosmologische theorie, die ΛCDM wordt genoemd – een versie van de algemene relativiteitstheorie met een kosmologische constante Λ, koude donkere materie (CDM, cold dark matter) en normale materie zoals de atomen die we kennen – lijkt goed te werken voor de meeste kosmologische verschijnselen. Maar deze theorie geeft een Hubbleconstante die op spanning staat met de experimentele waarde via de afstandsladder. Zitten er dan toch fouten in de afstandsladder? Naarmate de afstandsladder wordt verbeterd door nauwkeurigere metingen, komt de waarde van de Hubbleconstante niet of nauwelijks dichter in de buurt van de theoretisch voorspelde waarde. De consistentie waarmee astronomen een hogere waarde krijgen dan voorspeld door het ΛCDM-model, hint ernaar dat de oplossing dus niet eenvoudigweg is dat er iets mis is met de afstandsladder.
Een andere optie is dat wij ons bevinden in een superholte, een deel van het universum waar de energie- en materiedichtheid lager is dan het gemiddelde. Het gevolg van zo’n superholte is dat een vanuit daar gemeten Hubbleconstante lager uitvalt dan gemiddeld over het universum. De theoretische voorspelling van ΛCDM-model gaat juist over de gemiddelde Hubbleconstante. Dit zou een verklaring zijn voor de discrepantie, maar volgens het ΛCDM-model zouden zulke grote superholtes niet kunnen bestaan.
Astronomen en kosmologen zijn er dus nog niet over uit waarom de waardes zo ver uit elkaar liggen. Is ons ΛCDM-model toch niet de juiste beschrijving van ons universum? Zijn er toch meetfouten gemaakt bij de experimentele vaststelling van de Hubbleconstante? Tot de Hubbleconstanten zoals bepaald vanuit beide methodes binnen elkaars foutmarge liggen, blijft het een interessante open vraag welke oplossing de juiste is.