Vlak voordat Richard Hamming op een vrijdag in 1947 naar huis ging, zette hij een computer aan om gedurende het weekend een lange reeks berekeningen te doen. Maar toen hij maandag weer op zijn werkplek in Bell Laboratories terugkwam, bleek de berekening door een fout in de computer vroeg in het rekenproces in het honderd te zijn gelopen. Gefrustreerd ging Hamming aan de slag om te bedenken hoe de computer dergelijke fouten zelf kon corrigeren. Hij slaagde erin een oplossing te vinden en publiceerde in 1950 een artikel waarin hij de code presenteerde die tegenwoordig bekend staat als de “Hamming(7,4)-code”.
Fouten
Hoe werkt de Hamming(7,4)-code? Om dat te begrijpen, moet natuurlijk eerst duidelijk zijn wat een fout in een computer precies inhoudt. Stel je voor dat ik in Indonesië zit en een boodschap naar jou in Nederland wil versturen via een heel lange draad die wij tussen ons hebben gespannen. Mijn boodschap verstuur ik naar jou door ofwel hard met de draad te zwaaien, zodat er een grote golf ontstaat, ofwel zachtjes, met een kleine golf tot gevolg. Iedere keer dat de draad heftig heen en weer beweegt, noteer jij een 1, en iedere keer dat er maar een klein beetje beweging is, schrijf je een 0 op. Zo ontstaat er een code die jou – bijvoorbeeld in morsecode – vertelt wat mijn boodschap is. Als ik bijvoorbeeld vier keer zacht aan de draad heb getrokken is de code 0000 – vier keer “kort”.
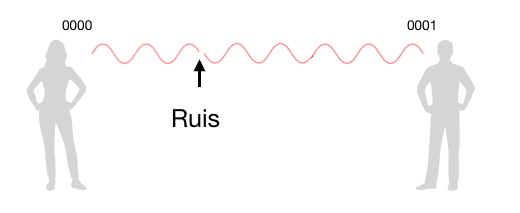
Afbeelding 1. Ruis op de lijn.Vanuit Indonesië verstuur ik de code 0000 naar jou. Ruis zorgt er echter voor dat het laatste getal van de code in een 1 verandert, waardoor jij denkt dat de boodschap 0001 is. Er zit een fout in de door jou genoteerde code!
Er ligt echter een probleem op de loer: de wind kan ervoor zorgen dat de draad veel heftiger heen en weer beweegt dan ik aanvankelijk veroorzaakte door er (zachtjes) aan te plukken. Hierdoor schrijf jij een 1 op terwijl ik een 0 bedoelde. Als de wind pas bij mijn laatste signaal aanwakkert, is de code die jij opschrijft bijvoorbeeld 0001. Dat is een andere code dan ik naar jou verstuurde! De wind, de ruis, dus, heeft voor een fout in de code gezorgd. En dit is precies wat er ook in de computer van Hamming gebeurde.
Van signalen versturen naar computeropslag
In het voorbeeld wordt een signaal verstuurd door het plukken aan een draad waarbij er twee opties zijn: hard plukken (1) en zacht plukken (0). Dat doet denken aan bits, waarbij er ook twee mogelijke waarden zijn: 1 of 0. Data-opslag in computers is volledig gebaseerd op zulke bits. Een bepaalde serie bits representeert bijvoorbeeld een bepaalde letter of een bepaald cijfer. Alles wat je op je computer opslaat – een tekst, een afbeelding, een audiobestand – wordt weergegeven door specifieke series van nullen en enen. In het voorbeeld geeft ieder getal uit de code die ik naar jou verstuur een bit weer. Je zou over het voorbeeld na kunnen denken alsof ik in Indonesië de gebruiker van de computer ben die bepaalde informatie op wil slaan. Die informatie wordt in het proces van het opslaan door ruis veranderd en jij, die de code ontvangt, bent de opslaglocatie van de computer. Door ruis is een van de bits van een 0 in een 1 veranderd: er heeft een bitflip plaatsgevonden, waardoor verkeerde informatie wordt opgeslagen.
Ruis in een computer
Maar wat is ruis in een computer precies? Bij een computer gaat het natuurlijk niet om wind die roet in het eten gooit. Ruis wordt gekarakteriseerd als “ieder proces dat een fout in een serie bits kan veroorzaken”. De ouderwetse computer die Hamming gebruikte, en het proces dat zijn berekening in de war schopte, geven een goed beeld van wat ruis in een computer kan zijn.

Afbeelding 2. Het maken van een ponskaart.Ponskaarten hebben gaten (1) en dichte plekken (0), de bits van de vroege computer.
De computers in de jaren 40 waren al gebaseerd op bits. De informatie werd destijds namelijk opgeslagen op ponskaarten, kartonnen kaarten waarop een 1 of een 0 werd gerepresenteerd door respectievelijk een gat of juist de afwezigheid van een gat op een bepaalde plaats. Fouten konden gemakkelijk ontstaan als bijvoorbeeld een van de hamertjes die de gaten maakten slecht gesmeerd was, waardoor het geen gat maakte terwijl het dat wel had moeten doen. Het omgekeerde was uiteraard ook mogelijk: dat er een gat werd gemaakt op een plek waar dat niet had gehoeven. De ruis die Hammings berekening in de war stuurde was het falen van een van de hamertjes. Door de gebrekkige werking van zulke hamertjes en de fouten die dat veroorzaakte, kon destijds het gehele systeem stil komen te liggen en moest er net zo lang gezocht worden tot de fout gevonden was, om die vervolgens handmatig te veranderen. De zelfcorrigerende code die Hamming bedacht was daarom een welkome vooruitgang in het computergebruik!
Pariteitsbits
De zelfcorrigerende code die Hamming bedacht is gebaseerd op het gebruik van de pariteitsbit. Pariteit geeft in deze context aan of een getal even of oneven is. De pariteitsbit laat zien of het aantal enen in de code even is – de pariteitsbit heeft dan een waarde van 0 – of oneven – de pariteitsbit heeft dan een waarde van 1. De code 0000 heeft geen enen: een even aantal (want nul is even), en dus is de waarde van de pariteitsbit 0. De code 0111 heeft drie enen, een oneven aantal enen, en daarom heeft de pariteitsbit de waarde 1.
Als ik aan iedere code die ik verstuur nu aan het einde een pariteitsbit toevoeg, kan jij gemakkelijk achterhalen of er ruis is geweest die een fout in de code heeft veroorzaakt. Stel dat ik de code 00000 verstuur, waarbij de vetgedrukte nul de pariteitsbit weergeeft. Neem aan dat er door ruis in het proces een enkele bitflip plaatsvindt op de derde bit waardoor de code die jij ontvangt 00100 is. De pariteitsbit geeft aan dat er een even aantal enen in de code had moeten zitten, maar zelf tel je een oneven aantal. Dat betekent dat er een fout in de code zit!
Het toevoegen van een pariteitsbit aan het einde van de code geeft wel aan dát er een fout in de code zit, maar niet wáár de fout zich bevindt[1]. Om de locatie van de fout te bepalen, zo bedacht Hamming, zijn er meerdere pariteitsbits nodig: voor iedere vier databits – de bits die de code vormen die ik jou vanuit Indonesië wil versturen – zijn drie pariteitsbits nodig. Dat geeft in totaal zeven bits, waarvan vier databits: (7,4).
Locatie-identifcatie
Hoe op deze manier de locatie van de fout gevonden kan worden, wordt duidelijk als we iedere pariteitsbit als een cirkel weergeven, cirkels die we p1, p2 en p3 noemen. Als we die cirkels laten overlappen, ontstaan er vier gebieden: d1, d2, d3 en d4, die we zien als de vier verschillende databits. Afbeelding 3a laat zien hoe dit eruit ziet. Als we de waarden van onze databits nu in de gebieden d1, d2, d3 en d4 plaatsen, zoals te zien in afbeelding 3b, wordt de waarde van elke pariteitsbit berekend door de drie databits die zich in deze cirkel bevinden als nieuwe code te beschouwen en daar de pariteit van te bepalen. In ons voorbeeld zien we bijvoorbeeld dat d1 = 0, d2 = 0 en d4 = 0, dus moet p1 = 0 zijn. Op dezelfde manier kunnen p2 en p3 bepaald worden.
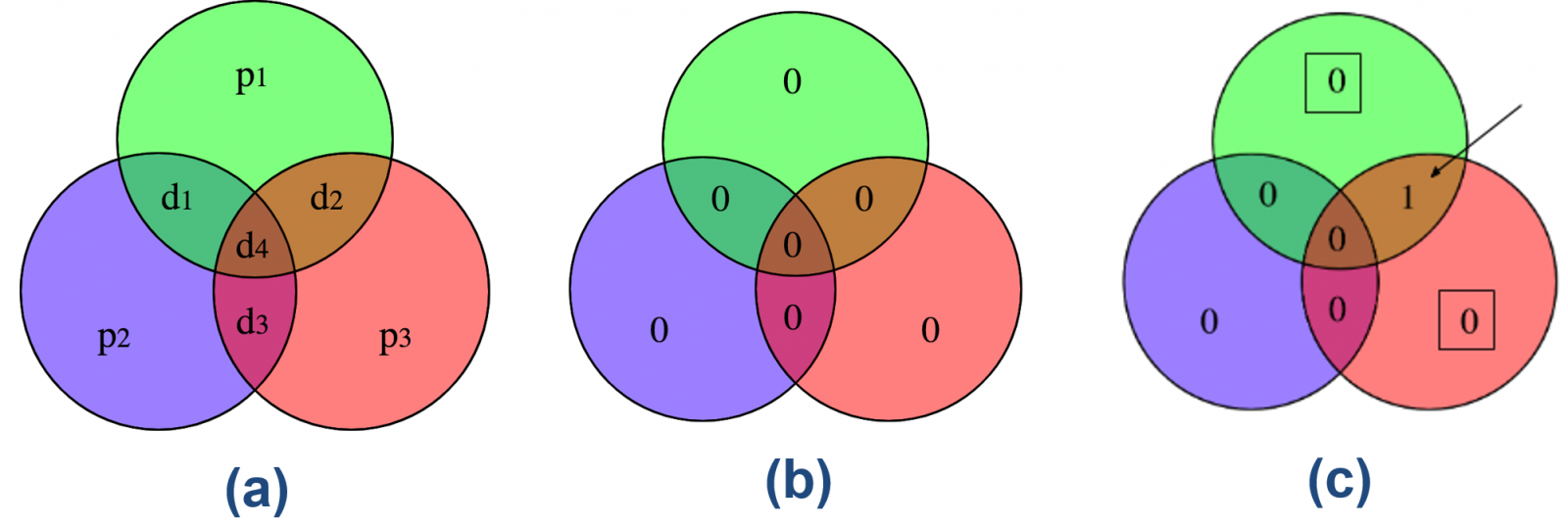
Afbeelding 3. De Hamming-code.(a) De drie pariteitsbits p1, p2 en p3, weergegeven als cirkels, en de vier databits d1, d2, d3 en d4 als de overlap van de deze cirkels. (b) Als de databits allemaal de waarde 0 hebben, dus als de code 0000 is, dan zijn de waarden voor de pariteitsbits ook allemaal 0. (c) Als er door ruis een bitflip bij databit d2 heeft plaatsgevonden, geven de pariteitsbits p1 en p3 niet de juiste waarde aan. Het gebied waar de cirkels p1 en p3 overlappen, geeft aan waar de fout is opgetreden. De computer kan deze fout nu zelf corrigeren door nogmaals een bitflip toe te passen op databit d2 zodat er op die locatie weer een nul komt te staan.
Stel nu dat er op locatie d2 een bitflip plaatsvindt, waardoor daar in plaats van een 0 een 1 te staan komt – zie afbeelding 3c. Dan zien we dat de pariteitsbits en niet de juiste waarde hebben, want d1 = 0, d2 = 1, d4 = 0, zou p1 = 1 moeten geven, en hetzelfde geldt voor p3. Het feit de pariteiten p1 en p3 niet kloppen, betekent dat de fout zit in het gebied waar deze cirkels elkaar overlappen, databit d2 dus! (De fout kan niet in d4 zitten, omdat dan ook de derde pariteitsbit een onjuiste waarde zou hebben.) Omdat iedere bit maar twee waarden kan aannemen, kan de computer databit d2 nu zelf van een 1 in een 0 veranderen.
Je ziet aan dit voorbeeld nog iets bijzonders: als er een fout in de code zit, zijn er minstens twee pariteitsbits die een onjuiste waarde krijgen. Het gevaar is daardoor erg klein dat er door fouten in de pariteitsbits zelf een correcte code juist “fout verbeterd” wordt: dat gebeurt pas als er in de drie controlebits maar liefst twee fouten sluipen.
Verrassend genoeg worden zelfcorrigerende codes vandaag de dag niet alleen in de informatica gebruikt: ook in de natuurkunde kom je ze op allerlei plaatsen tegen. Zelfs een mogelijke beschrijving van quantumzwaartekracht blijkt veel met zelfcorrigerende codes te maken te hebben! Maar goed, het zou nu te ver voeren om dat in detail uit te leggen – meer daarover schrijven we later nog eens op deze site.
Vanaf het moment dat Hamming zijn foutcorrigerende code had bedacht, werden aan iedere vier databits in een code drie extra pariteitsbits toegevoegd. Zo konden computers vanaf 1950 fouten dus zelf detecteren, opsporen en corrigeren – en kon Hamming op vrijdagen met een gerust hart naar huis gaan nadat hij een ingewikkelde berekening aan had gezet.
Meer weten over dit onderwerp? Dit artikel is gebaseerd op deze YouTube-video van Art of the Problem. Op Wikipedia kun je nog veel meer lezen over Hammingcodes.
[1] Er vanuit gaande dat de ruis maar één enkele bitflip veroorzaakt kan hebben, had de originele code een van de volgende kunnen zijn: 1010, 0110, 0011 of 0000.