Afbeelding 1. Het universum.Een klein stukje van het hele universum. Kunnen we een quantummechanische golffunctie vinden die het hele heelal beschrijft? Foto: NASA.
Golffuncties
Voordat we de diepte in gaan en ik het gehele artikel van Hartle en Hawking uitleg, wil ik eerst het concept golffunctie nader toelichten. De golffunctie is een quantummechanisch begrip dat al sinds de jaren 20 van de vorige eeuw bestaat. Het begrip vormt de kern van de quantummechanica. Een golffunctie vertelt je met welke kans je een deeltje, bijvoorbeeld een elektron, kunt aantreffen op een gegeven punt in de ruimte en in de tijd.
Je kunt met behulp van de golffunctie allerlei interessante dingen uitrekenen, zoals bijvoorbeeld de gemiddelde afstand tussen een elektron en een proton in het waterstofatoom. De golffunctie voldoet ook aan een vergelijking, een zogeheten differentiaalvergelijking, die we de Schrödingervergelijking noemen. Door de Schrödingervergelijking op te lossen, kun je de golffunctie vinden voor bijvoorbeeld het elektron in een waterstofatoom.
Hoewel de Schrödingervergelijking er vrij eenvoudig uitziet, is deze vergelijking vaak niet exact op te lossen en moeten er benaderingen gemaakt worden. Toch is er één exact bekende oplossing die erg bepalend is voor de natuurkunde, namelijk de golffunctie van de “quantum-harmonische oscillator”. Dit is de quantummechanische versie van een massa die aan een veer heen-en-weerbeweegt. De quantum-harmonische oscillator kent vele toepassingen in de natuurkunde en staat centraal in de quantumveldentheorie.
Een belangrijke eigenschap van de harmonische oscillator is dat de golffunctie voor de toestand van het systeem met de laagste energie, de vorm van een normaal- of gaussische verdeling aanneemt met een bepaalde variantie en een gemiddle van nul, zoals hieronder weergegeven in afbeelding 2. De positie van het massieve deeltje aan de “quantumveer” zal dus met grote kans ongeveer x = 0 zijn (uitwijking nul), maar er is ook een kleine kans dat het deeltje zich verder weg van de evenwichtstoestand bevindt.
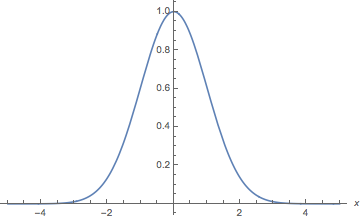
Afbeelding 2. Normaalverdeling. De golffunctie van de laagste-energietoestand in de quantummechanische verise van de slinger ziet eruit als de normaal- of gaussische verdeling die hierboven geschetst is. In de buurt van de evenwichtsstand (x=0) is de kans groot om het deeltje aan te treffen; verder weg is die kans kleiner.
Voor de opvolger van de quantummechanica, de quantumveldentheorie, is de golffunctie van de toestand met de laagste energie ook vaak een normaalverdeling. Als je dus geïnteresseerd bent in de grondtoestand van een systeem, dan is de beste gok om naar een golffunctie zoals die hierboven te zoeken. Dit is precies wat Hartle en Hawking deden, maar dan voor een theorie waarvan we helemaal niet zeker weten of die als quantumveldentheorie beschreven kan worden: de theorie van de zwaartekracht!
De golffunctie van het universum
De missie die Hartle en Hawking voor zichzelf uitstippelden, was niet het vinden van de golffunctie voor een enkel deeltje aan een quantumveer, maar voor het hele universum! Die golffunctie beschrijft dus niet de kans op een bepaalde positie van een elektron, maar de kans op een bepaald heelal. Maar de kans als functie van wat dan – van iets als positie? Nee: ook al lijkt het vaak zo dat het universum in bijvoorbeeld Amsterdam Oost en West totaal anders zijn, natuurkundig gezien zijn die plaatsen onderdeel van een en hetzelfde heelal.
Hartle en Hawking kamen op het idee om de golffunctie van het heelal niet van positie, maar van randvoorwaarden aan het begin van de tijd te laten afhangen. Ze noemden de begintijd van ons universum t = 0 en bekeken de situatie waarin op die tijd het universum een bepaalde vorm aannam en een specifieke kromming had. Aan de hand van een gedetaileerde analyse van die keuzes en de gevolgen ervan in de quantummechanica konden Hartle en Hawking de kans op elke specifieke begintoestand uitrekenen, en zo een mogelijke golffunctie van het universum bepalen.

Afbeelding 3. James Hartle en Stephen Hawking.Foto’s: Luboš Motl / Philip Waterson, LBIPP, LRPS.
Deze functie had wederom de vorm van een normaalverdeling en kon dus gezien worden als een golffunctie voor een laagste-energietoestand. Daarmee bleek het mogelijk om allerlei kosmologische aspecten van het heelal te beschrijven. Bovendien had deze golffunctie een erg belangrijke eigenschap; het was namelijk een oplossing van de zogeheten Wheeler-DeWittvergelijking voor zwaartekracht. Die vergelijking is het analagon van de Schrödingervergelijking in de zwaartekrachtstheorie van Einstein, en vormt de basis voor een quantummechanische studie van zwaartekracht. Kortom: de golffunctie die Hartle en Hawking vonden voldeed aan diverse belangrijke eisen.
Het universum zonder begin
Naast het produceren van een mogelijke golffunctie van het universum, hebben Hartle en Hawking met hun randvoorwaarden in zekere zin ook het begin van het universum hergedefinieerd. Door de technieken die Hartle en Hawking gebruikten tijdens hun berekening goed te bestuderen, zie je namelijk dat het universum in hun beschrijving op een zeer bijzondere manier begon; het begon zonder enig begin! Dit klinkt natuurlijk absurd, maar zo gek is het nog niet.
Je kunt zo’n “begin zonder begin” als volgt voorstellen. Stel je voor dat het universum de vorm heeft van een cilinder, waarbij de rechte tijdrichting langs de cilinder loopt, en de cirkel om de cilinder heen de ruimte op één bepaald tijdstip voorstelt. Op het ene uiteinde van de cilinder is het de dag van vandaag en op het ander het het tijdstip dat we t = 0 hebben genoemd. Hartle en Hawking wilden echter het universum niet precies op dat moment t = 0 laten beginnen: ze rekenden als het ware “verder terug” door aan dat uiteinde van de cylinder nog eens een halve bol te plakken. Daarmee “begint” de tijd dus niet echt ergens meer – net zomin als je op aarde kunt zeggen dat de aarde “begint” op de zuidpool – dat is een gewone plek op aarde, net als elk ander punt. Op die manier begint het universum dus ook “uit het niets” en zonder enig begin!
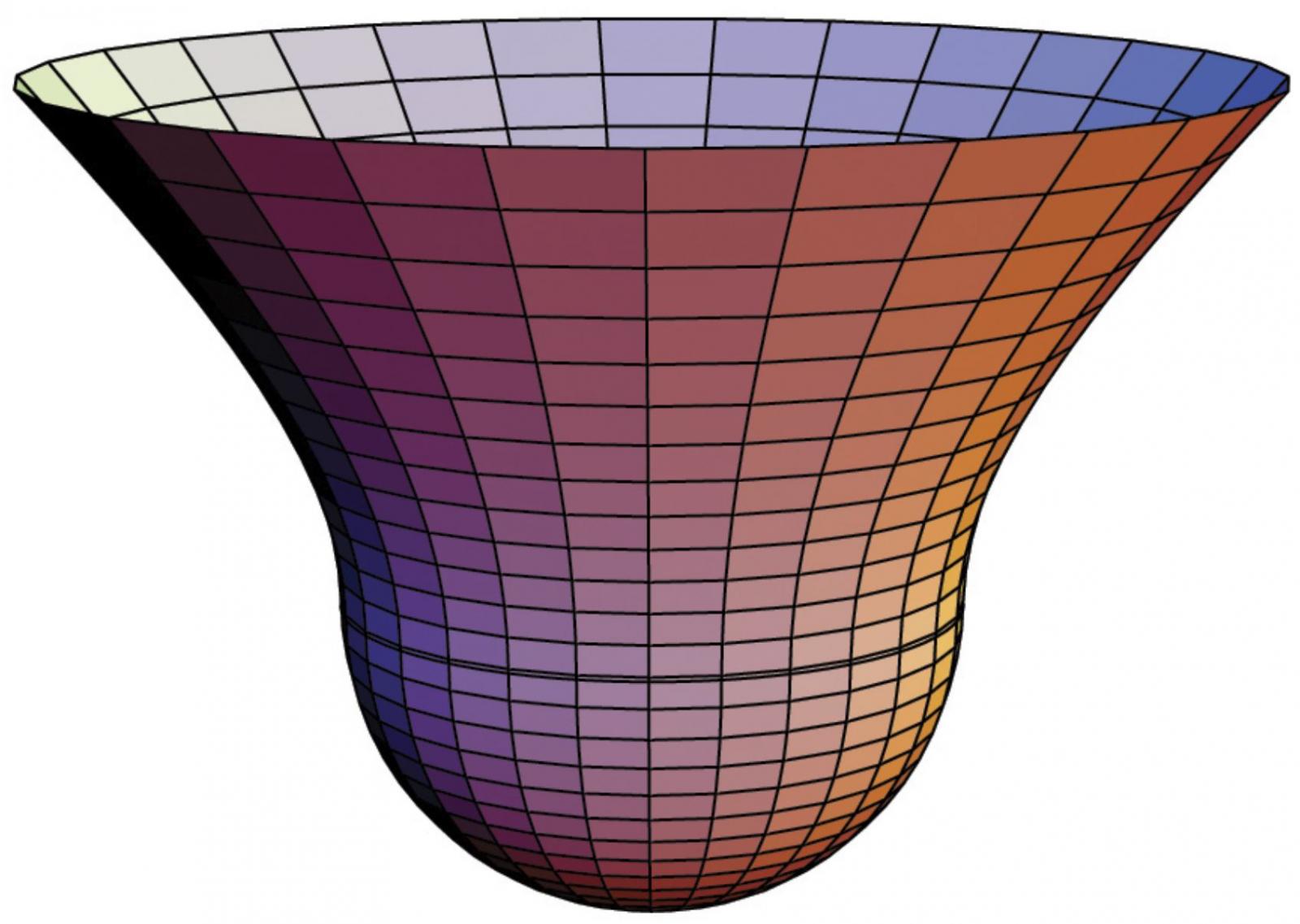
Afbeelding 4. Een begin zonder begin.Afbeelding: KITP Santa Barbara.
De golffunctie van vandaag
Tot op de dag van vandaag speelt de golffunctie van Hartle en Hawking een belangrijke rol in de kosmologie en in ons begrip van zwaartekracht. Verschillende onderzoeksgroepen, waaronder de kosmologiegroep in Amsterdam, werken aan het begrijpen en generaliseren van het originele werk van Hartle en Hawking. Over of hun beschrijving namelijk precies klopt, en echt de golffunctie van ons eigen universum oplevert, zijn de geleerden het nog lang niet eens. Hoewel we nog steeds niet goed begrijpen hoe quantumzwaartekracht werkt en wat de precieze implicaties zijn van het voorstel van Hartle en Hawking, geeft hun golffunctie hoe dan ook een opstapje naar de volledige quantumtheorie van de zwaartekracht die we ooit hopen te vinden.
