Geen categorie

De examenvraag die iedereen fout deed

2 min

De SAT’s zijn de bekende toelatingstesten voor hogescholen en universiteiten uit de Verenigde Staten. Het examen is een meerkeuzetoets van 3 uur, bestaande uit 3 verschillende onderdelen: lezen, schrijven & taal, en wiskunde. Elk jaar proberen studenten een zo hoog mogelijke score te halen, om vervolgens binnen te komen bij goede universiteiten. De test wordt door sommigen goed gemaakt en door sommigen minder goed, maar in 1982 gebeurde er wel iets heel typisch: er was één vraag die iedereen fout had. En daarmee bedoel ik ook: iedereen – zowel de studenten als de makers van de toets – want het goede antwoord stond niet eens tussen de meerkeuzeopties.

SAT
De SAT-vraag die iedereen fout deed. Hoe vaak moet de kleine cirkel ronddraaien om weer op zijn oorspronkelijke plaats terug te komen?

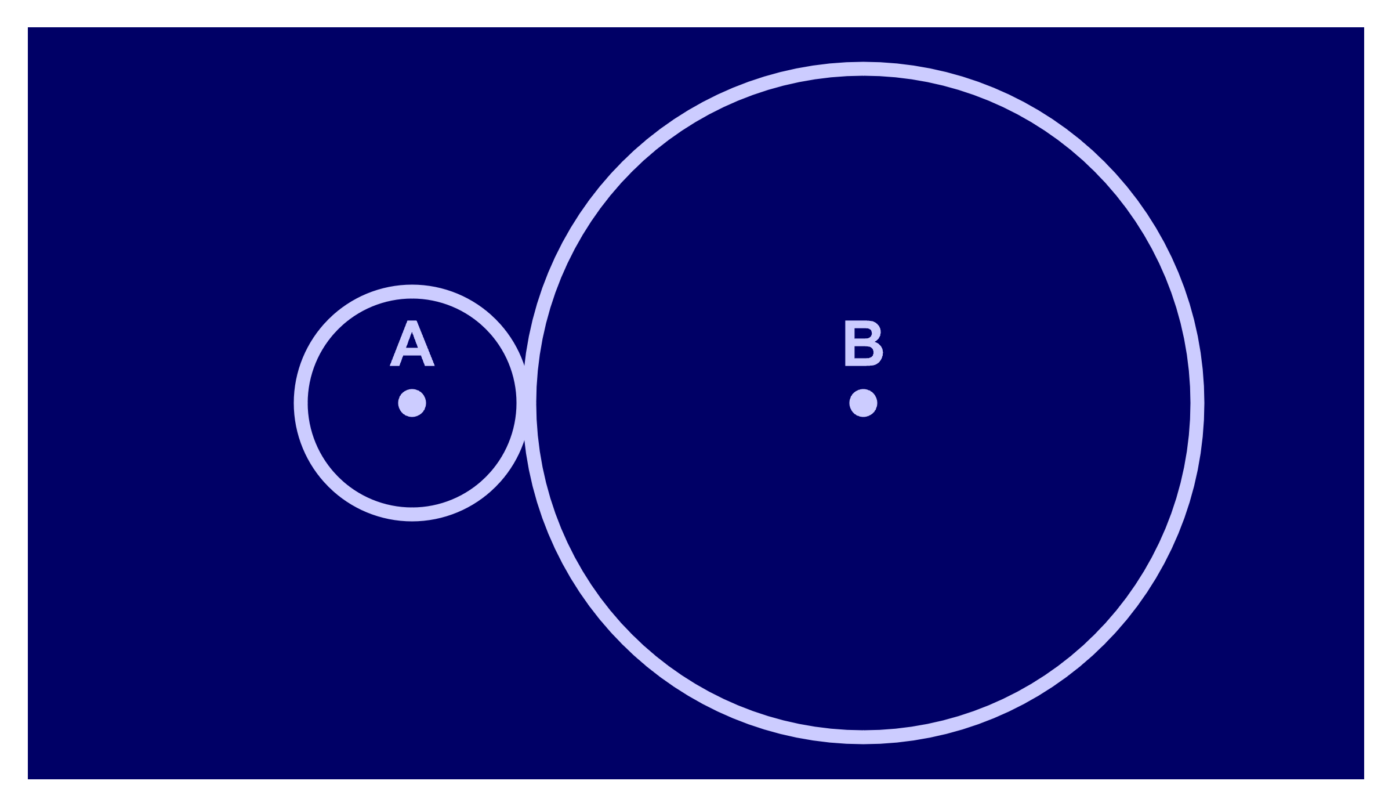
De vraag was de volgende: stel dat twee cirkels naast elkaar en tegen elkaar aan liggen – zie de afbeelding. Links zie je cirkel A, en rechts cirkel B. De straal van cirkel A is 1/3 keer die van cirkel B. Vervolgens rolt cirkel A om cirkel B, en is de vraag: hoeveel omwentelingen moet cirkel A maken om weer op zijn originele startpositie uit te komen? De antwoordopties waren als volgt: A) 3/2, B) 3, C) 6, D) 9/2, E) 9.  Voor je verder leest: welk antwoord zou jij geven?

Op het eerste oog klinkt antwoord B, 3 omwentelingen, heel logisch. Als de straal 3 keer groter is, is de omtrek dat ook, dus is het logisch dat cirkel A 3 keer moet roteren rondom cirkel B.

Toch klopt dat niet! Wat het goede antwoord dan wel is? Daar zocht het YouTube-kanaal Veritasium uit in deze video:

Wiskunde

Download PDF