
Afbeelding 1. Paul Ehrenfest.De Oostenrijks-Nederlandse natuurkundige Paul Ehrenfest (1880-1933) bedacht in 1909 een gedachte-experiment dat de speciale relativiteitstheorie leek tegen te spreken. De oplossing van de paradox leidde uiteindelijk tot de algemene relativiteitstheorie. Portret uit de Dibner Library of the History of Science and Technology.
We schrijven 1909, een jaar vrijwel midden tussen het voltooien van Einsteins speciale en zijn algemene relativiteitstheorie. In de eerste theorie heeft Einstein laten zien dat ruimte en tijd niet zijn wat we altijd gedacht hebben: geen twee onafhankelijke grootheden, maar twee componenten van de “ruimtetijd”, een geheel dat iedere waarnemer op zijn eigen manier opdeelt in ruimte en tijd. Afstanden en tijdsintervallen zijn niet meer absoluut. Ze zijn relatief geworden: afhankelijk van hoe – en in het bijzonder: met welke snelheid – je ze waarneemt.
Lorentzcontractie
De gevolgen van Einsteins nieuwe wereldbeeld, uitgebreid beschreven in ons dossier over relativiteitstheorie, zijn in 1909 inmiddels bekend. Een van die gevolgen is Lorentzcontractie: het feit dat bewegende voorwerpen korter lijken te worden dan ze in stilstand zijn. Met behulp van dit verschijnsel en het verwante begrip van tijddilatatie kon Einstein verklaren wat Albert Michelson en Edward Morley experimenteel hadden waargenomen: voor iedere waarnemer is de lichtsnelheid hetzelfde. In éen van jouw secondes legt een lichtstraal altijd zo’n 300 miljoen van jouw meters af – ondanks dat die meters en secondes soms helemaal niet overeenkomen met die van een ander.
De nieuwe manier van kijken naar ruimte en tijd is verwarrend, maar lijkt tegelijkertijd prachtig te kloppen. Dat wil zeggen: totdat de Oostenrijks-Nederlandse natuurkundige Paul Ehrenfest een gedachte-experiment bedenkt waarvan niet direct duidelijk is hoe het te rijmen valt met Einsteins speciale relativiteit. Het idee van Ehrenfest is simpel: neem een stevige, ronde schijf, laat die in gedachten zo snel draaien dat de rand van de schijf bijna de lichtsnelheid bereikt, en vraag je af hoe verschillende waarnemers dit proces ervaren.
Een draaiende schijf
Einstein zelf formuleert het probleem later als volgt: vergelijk een waarnemer die stilstaat (wat wil zeggen dat de schijf ten opzichte van hem met enorme snelheid draait) en een waarnemer die ergens op de schijf staat en meedraait. Hoe zien deze twee waarnemers de schijf?

Afbeelding 2. Een draaimolen.Ehrenfests paradox gaat over twee waarnemers en een grote draaiende schijf – een soort draaimolen, maar dan een waarvan de rand met bijna de snelheid van het licht beweegt. Foto: Wikipedia-gebruiker Oxyman.
Om te beginnen is het probleem volkomen rotatiesymmetrisch: vanuit het midden van de schijf gezien is er geen enkele bijzondere richting op de schijf. Als gevolg daarvan moeten beide waarnemers de schijf nog steeds als een perfecte cirkel zien. Het enige waarover de waarnemers dus van mening zouden kunnen verschillen, is wat de straal of de omtrek van die cirkel zijn.
Nu had Einstein al aangetoond dat Lorentzcontractie alleen gebeurt in de richting waarin zaken bewegen: als een trein met hoge snelheid langsrijdt zal die trein in de lengte, dus in de richting waarin hij beweegt, iets korter lijken – maar de hoogte van de trein zal voor een waarnemer op het perron niet veranderen. Het argument is eenvoudig: als ik vanaf het perron iemand in de trein, die precies even lang is als ik, een high five wil geven, moeten we (gesteld dat onze voeten op dezelfde hoogte staan) onze handen ook precies even hoog houden. Waarom? Zou ik mijn hand hoger moeten houden en de ander zijn hand lager, dan volgt namelijk een tegenspraak: vanuit de trein gezien beweeg ik immers met grote snelheid, en dus zou voor de waarnemer in de trein ik juist mijn hand lager moeten houden. Deze tegenspraak kan alleen opgelost worden door te concluderen dat de hoogte van bewegende voorwerpen dus niet verandert als ze gaan bewegen – alleen de lengte doet dat.
Langer of niet?
Hoe zit dat nu bij onze draaiende schijf? Hier is het niet de hoogte maar de straal van de cirkel die loodrecht op de bewegingsrichting staat. Noch voor de stilstaande waarnemer, noch voor degene die met de schijf meedraait, zou die straal dus moeten veranderen. Of beter gezegd: áls de straal al verandert – de schijf kan natuurlijk door de hoge draaisnelheid en de bijbehorende centrifugale kracht best wat uitzetten – moeten beide waarnemers in ieder geval dezelfde verandering zien. Beide waarnemers zien uiteindelijk dus een cirkel met dezelfde straal; laten we die straal R noemen.
De paradox ontstaat nu als we proberen te bedenken wat er gebeurt met de omtrek van de cirkel. Laten we beginnen met de waarnemer die van een afstandje naar de draaiende schijf staat te kijken. Hij ziet zoals gezegd een perfecte cirkel, en we weten sinds de middelbare school dat er een eenvoudig verband is tussen de straal R van een cirkel en zijn omtrek: O = 2πR. Heeft onze schijf bijvoorbeeld een straal van 100 meter, dan is de omtrek zo’n 628 meter.
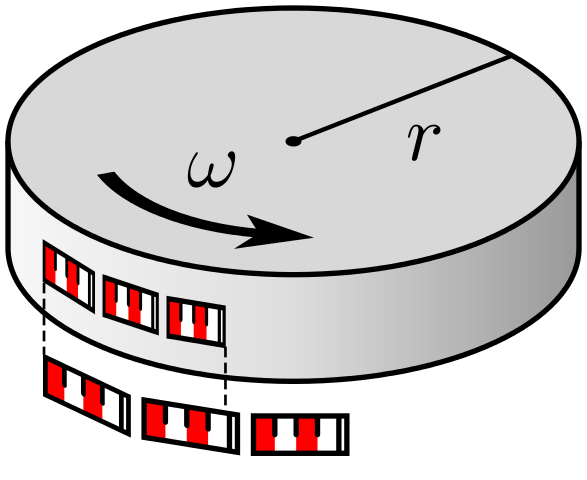
Afbeelding 3. De schijf van Ehrenfest.De paradox van Ehrenfest ontstaat als we ons afvragen hoe groot de omtrek van de schijf volgens de twee waarnemers is.
Stel nu dat de meedraaiende waarnemer een aantal meetlatten van percies een meter bij zich heeft, en die in de lengterichting langs de rand van de schijf plakt. Hier komt de Lorentzcontractie in het spel: doordat de meetlatten in de lengterichting bewegen, zal de stilstaande waarnemer die meetlatten korter zien. Draait de rand van de schijf bijvoorbeeld met 180.000 kilometer per seconde, zo’n drie vijfde van de lichtsnelheid, dan zal de stilstaande waarnemer meetlatten zien die voor hem zo’n 80 centimeter lang lijken. Van die meetlatten passen er ruim 785 rond de omtrek van iets meer dan – voor hem – 628 meter. Maar voor de meedraaiende waarnemer zijn de meetlatten zoals gezegd een meter lang – voor hem heeft de schijf dus een omtrek van maar liefst 785 meter!
Daarmee zijn we op een tegenspraak gestuit. We hebben nu immers drie beweringen gedaan:
- Ook voor de meedraaiende waarnemer is de schijf een perfecte cirkel,
- Ook voor de meedraaiende waarnemer heeft de schijf een straal van 100 meter,
- Voor de meedraaiende waarnemer heeft de schijf een omtrek van zo’n 785 meter.
Hoe zijn die drie beweringen te rijmen met het feit dat voor elke cirkel de omtrek gelijk is aan 2πR? De omtrek lijkt voor de bewegende waarnemer veel groter te zijn dan dat – ondanks dat de straal van de cirkel niet verandert!
De oplossing van de paradox
Ehrenfests paradox lijkt de ideeën van de speciale relativiteitstheorie op losse schroeven te zetten: met een eenvoudig argument komen we tot een schijnbaar onherstelbare tegenspraak. Maar is dat ook echt zo? Gelukkig niet, want er zijn maar liefst twee aannames in het bovenstaande verhaal hebben die we nog eens goed nader moeten bekijken.
Ten eerste hebben we hierboven Einsteins speciale relativiteitstheorie toegepast in een situatie waar die theorie niet vanzelfsprekend geldig is. Voor de stilstaande waarnemer is er niets aan de hand, maar voor de meedraaiende waarnemer wel. Draaien is namelijk een vorm van versnellen: elke beweging die niet langs een rechte lijn gebeurt, is een versnelling. Ga maar eens met een kop koffie in een draaimolen zitten: het zal snel duidelijk zijn dat er bij draaien sprake is van versnelling. Nu ging Einsteins speciale relativiteitstheorie heel specifiek over waarnemers die met een constante snelheid bewegen; is die theorie dus wel geldig voor de meedraaiende waarnemer? En zo niet, hoe moeten we de situatie voor die waarnemer dan wel beschrijven?
Het algemene antwoord op die vraag besefte Einstein volgens de overlevering juist door deze paradox, en het leidde hem uiteindelijk, zes jaar later, tot zijn algemene relativiteitstheorie. De tweede aanname in ons verhaal hierboven is namelijk dat de omtrek van een cirkel altijd gelijk is aan 2π maal zijn straal. In een plat vlak is dat ook het geval, maar op een gekromd oppervlak hoeft dat beslist niet zo te zijn! Denk aan een breedtecirkel op de aarde: zo’n cirkel heeft de Noord- of Zuidpool als middelpunt, maar de omtrek is niet 2π maal de afstand (gemeten over het kromme aardoppervlak) tot dat middelpunt! De evenaar is bijvoorbeeld zo’n 40.000 kilometer lang, maar de afstand tot de Zuidpool is 10.000 kilometer – de verhouding tussen straal en omtrek is een factor 4, veel minder dan 6,28! Op een gekromd oppervlak – of algemener: in een gekromde driedimensionale ruimte – gelden meetkundige wetten als O = 2πR niet meer.

Afbeelding 4. Cirkels op een bol.De afstand van de “breedtecirkels” op een bol tot de dichtstbijzijnde pool is groter dan de afstand van een cirkel in het platte vlak tot zijn middelpunt. Afbeelding: Wikipediagebruiker Geek3.
Uiteindelijk plakte Einstein deze twee ideeën aan elkaar: zijn oplossing voor de paradox was dat versnelde waarnemers kennelijk geen vlakke ruimte (of nog preciezer: geen vlakke ruimtetijd) ervaren. Versnelling was volgens Einstein nauw verbonden kromming – en dat idee gebruikte hij uiteindelijk om in zijn algemene relativiteitstheorie ook de zwaartekrachtsversnelling te beschrijven als een kromming van de ruimtetijd.
De meedraaiende waarnemer op de schijf ervaart dus een gekromde ruimte. Tegenwoordig weten we ook precies hoe we die gekromde ruimte moeten beschrijven: de afstanden in zo’n ruimte kunnen niet berekend worden met eenvoudige wetten als O = 2πR, maar met een meetkundig recept dat bekend staat als de Langevin-Landau-Lifschitzmetriek. De bijbehorende kromme ruimte is lastig in drie dimensies weer te geven, in tegenstelling tot de kromming van de aardbol. Het verschil is dat daar de verhouding tussen omtrek en straal kleiner is dan 2π – zoals we gezien hebben in het voorbeeld van de evenaar – maar in het voorbeeld van de draaiende schijf juist groter. Toch kunnen we met een truc wel een plaatje maken: als we onzelf toestaan om gelijke oppervlaktes in onze afbeelding niet overal even groot weer te geven kunnen we de Langevin-Landau-Lifschitzruimte weergeven in een plaatje dat erg lijkt op afbeelding 5 hieronder: het hyperbolische vlak. We zien in dit plaatje inderdaad dat op grotere afstand van het middelpunt het aantal driehoeken op een cirkel snel toeneemt: de verhouding tussen straal en “omtrek” is inderdaad groter dan 2π. Helemaal waarheidsgetrouw is dit beeld niet, maar het komt dicht in de buurt.

Afbeelding 5. Het hyperbolische vlak.Afbeelding: Tom Ruen.
Wie nog preciezer wil ervaren hoe de gekromde Langevin-Landau-Lifschitzmetriek eruit ziet, kan misschien het beste zelf een supersnel draaiende schijf bouwen en erop gaan staan – maar zoals bij veel gedachte-experimenten is dat nog niet zo eenvoudig… Dat is natuurlijk ook de kracht van gedachte-experimenten: ook zonder het bouwen van grote, dure en soms vrijwel onmogelijke apparatuur kunnen ze ons toch veel leren over de natuur.