
Zo kennen we bijvoorbeeld Simulated Annealing (letterlijk vertaald: ‘gesimuleerd uitgloeien’) als optimalisatie-algoritme. Geïnspireerd op de thermodynamica en het afkoelen van metalen, wordt de boltzmannverdeling, een statistische techniek, gebruikt om met willekeurige, steeds preciezere stapjes een steeds betere oplossing van een probleem te vinden.
Een ander voorbeeld zijn zogenaamde diffusiemodellen, die een belangrijke rol spelen in de hedendaagse generatieve AI – de kunstmatige intelligentie die allerlei vormen van nieuwe output genereert. Een dergelijk model is geïnspireerd op het natuurkundige concept van diffusie, waarbij deeltjes zich willekeurig door een medium bewegen, zoals een druppel inkt zich in een glas water verspreidt. In de AI kunnen deze stochastische2 processen worden gebruikt om nieuwe, realistische data te genereren, zoals afbeeldingen, tekst of geluid. Misschien heb je wel eens gespeeld met Dall·E (foto), Sora (video) of Suno (audio). Allemaal modellen die onder de motorkap gebruikmaken van diffusie!
In de natuurkunde beschrijft diffusie op grote schaal hoe een substantie zich verspreidt van een plek met hoge concentratie naar een plek met lage concentratie, zonder gerichte beweging. Naast het voorbeeld van de inktdruppel kun je bijvoorbeeld denken aan de verspreiding van melk in je koffie, een olievlek op water of de terugstroom van ionen door een celmembraan na het opbouwen van een potentiaal (een elektrische spanning) door een natrium-kaliumpomp.
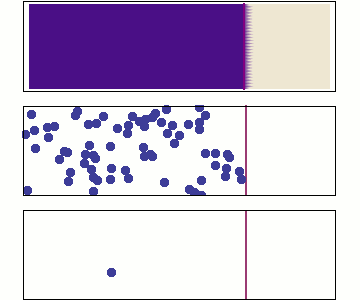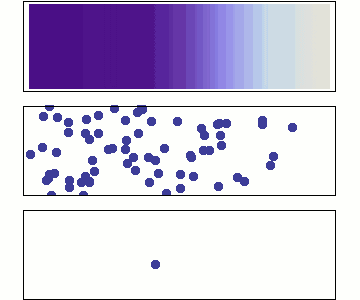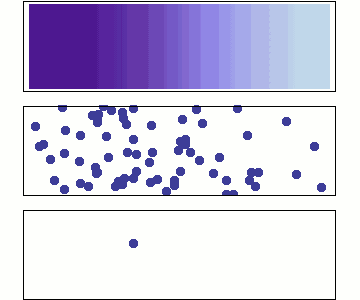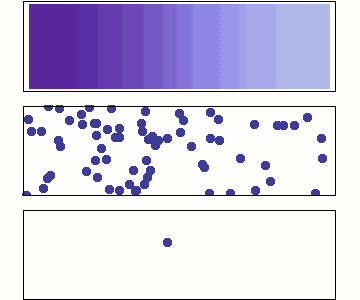
Op atomair niveau wordt diffusie beschreven door een random walk, of ‘dronkemanswandeling’, van minuscule deeltjes. Door een veeltal onderlinge botsingen en interacties lijkt elk individueel deeltje zich willekeurig te bewegen.
Zo’n dronkemanswandeling is wiskundig te vatten in een bijzonder simpel stochastisch model. Als we alle complexe onderliggende interacties achterwege laten, is de beweging niets anders dan het herhaaldelijk nemen van kleine stapjes in een willekeurige richting. Als de wandeling in één dimensie gebeurt – langs een lijn, dus – heeft een random walk bij elke tijdstap evenveel kans om naar links of naar rechts te stappen. In een tweedimensionaal rooster ziet zo’n wandeling er bijvoorbeeld als volgt uit:
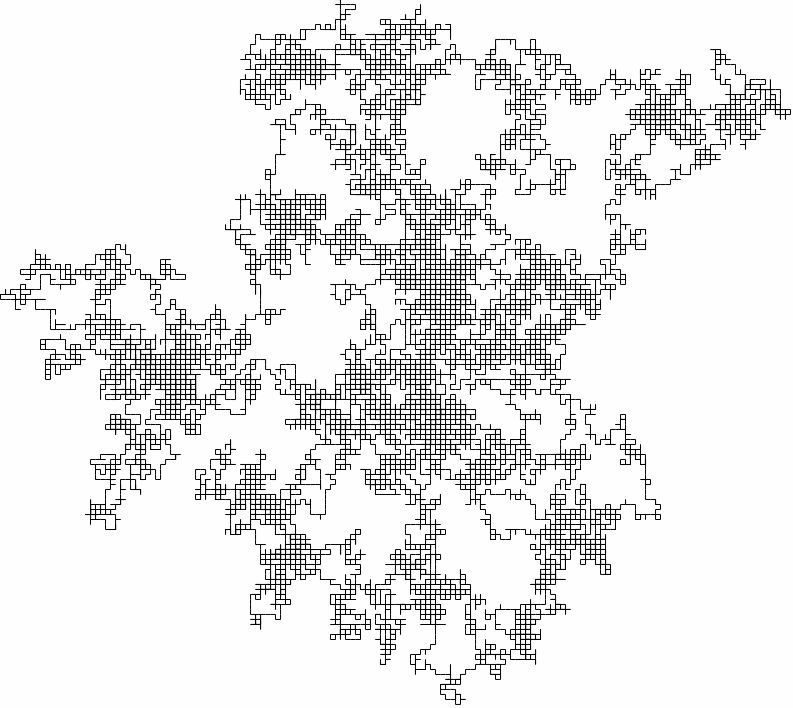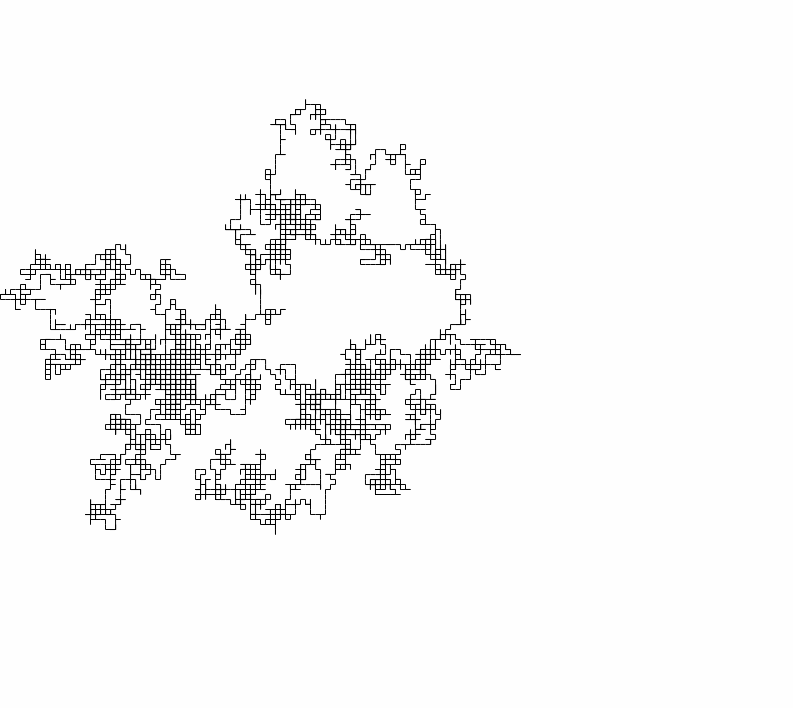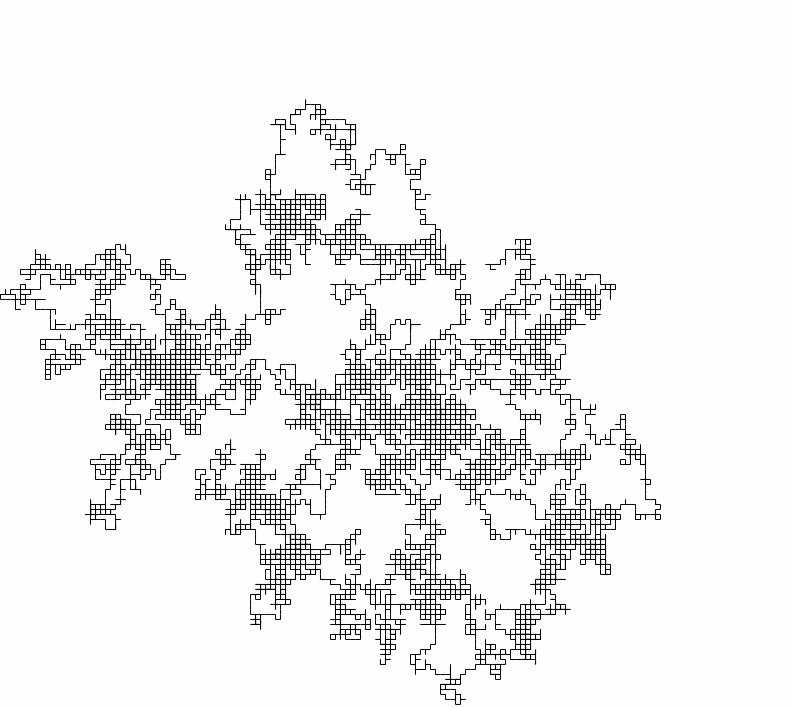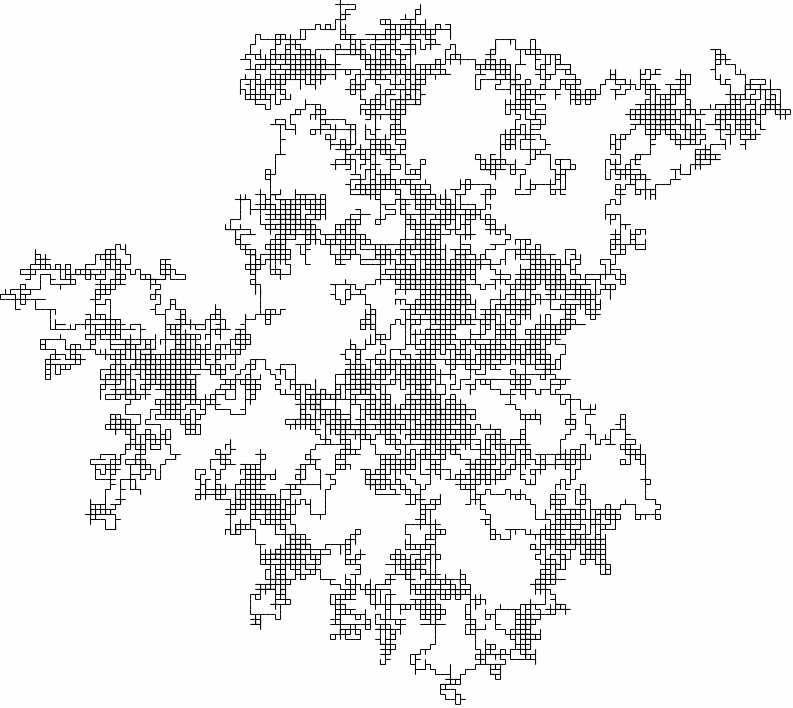
Dit bijzonder eenvoudige model is in staat een breed scala aan willekeurige processen te beschrijven, zonder het onderliggende systeem te hoeven doorgronden. Het kan bijvoorbeeld het pad beschrijven dat een grazende koe aflegt, of de fluctuatie op de aandelenbeurs, of de winsten en verliezen van een gokker. Een interessant resultaat van de dronkemanswandeling is het volgende: naarmate de dronkaard meer stappen zet, komt hij steeds verder van huis, maar gaat hij nergens naartoe. Hoewel de spreiding van de verdeling van mogelijke eindposities toeneemt met het aantal stappen3, blijft de gemiddelde afgelegde afstand 0. De uitkomsten van een dronkemanswandeling zijn normaal verdeeld: de kans vertoont een piek rond nul en valt geleidelijk af in de vorm van een (toren-) klok, en wordt ook wel eens een bell-curve genoemd.
Hoe valt dit alles nu samen met de diffusiemodellen die gebruikt worden in de AI?
Een diffusiemodel is een computermodel dat getraind wordt om de dronkemanswandeling om te draaien. We proberen de weg terug naar huis van de dronkaard te vinden. Dit is een bijzonder moeilijk probleem: ons model van de random walk heeft namelijk helemaal geen besef van richting of historie. Elke toestand is simpelweg een product van aaneengesloten willekeurige stapjes. Het is als het ontroeren van een pot verf of glas limonade. Een dergelijk probleem wordt ook wel een inverse probleem genoemd.
Bij het trainen van een diffusiemodel wordt geleidelijk ruis toegevoegd aan data, zoals een afbeelding, totdat de oorspronkelijke data volledig is “verstrooid” en er alleen ruis overblijft. Dit proces noemen we voorwaartse diffusie. In essentie is voorwaartse diffusie een random walk door een hoogdimensionale ruimte. Door een afbeelding te verstrooien, bewegen we door een ruimte die gevormd wordt door alle mogelijke pixelwaarden voor elke pixel: een ruimte die elk mogelijk plaatje dat bestaat en dat ooit gaat bestaan, omvat! Deze stapsgewijze verstrooiing gebruiken we om ons AI-model te trainen.
Video. Animatie van diffusie als random walk in pixel space. Clip (van 08:20-09:45) uit een uitstekend praatje van Miika Aittala over diffusiemodellen. Hele video: https://youtu.be/T0Qxzf0eaio?si=8WLfz0N_U2Civd7F Bijbehoren artikel: https://arxiv.org/abs/2206.00364.
Het omgekeerde proces, achterwaartse diffusie, is de crux van diffusiemodellen. Het is heel moeilijk om direct te voorspellen wat voor plaatje er onder heftige ruis verscholen ligt, maar het is makkelijker om de computer te vragen telkens een beetje ruis weg te halen. Hierbij wordt de ruis dus stapsgewijs teruggedraaid. Uiteindelijk houden we de computer voor de gek door hem een afbeelding met alleen maar ruis voor te schotelen. Het algoritme gaat dan stapsgewijs steeds meer detail in de afbeelding ‘dromen’, totdat een plaatje van bijvoorbeeld een kat of hond overblijft. Zo wordt uit de ogenschijnlijk willekeurige chaos nieuwe data opgebouwd. Deze data kan een fotorealistische afbeelding zijn, een video, of zelfs een muziekstuk –afhankelijk van wat voor data de computer tijdens het leren gezien heeft.

Diffusiemodellen tonen aan hoe fundamentele concepten uit de natuur- en wiskunde kunnen leiden tot baanbrekende ontwikkelingen in de kunstmatige intelligentie. Door gebruik te maken van stochastische processen zoals de dronkemanswandeling, zijn we in staat om uit pure ruis betekenisvolle en vaak verbluffende creaties te distilleren. Zo blijkt maar weer eens dat zelfs de meest complexe systemen terug te leiden zijn tot eenvoudige, elegante ideeën.
[1] Let wel, binnen de Nobelprijzen is er geen categorie voor informatica of wiskunde. Dit jaar ging wel ook de Nobelprijs voor Scheikunde naar AI-gerelateerd onderzoek.
[2] Statistische processen die aan een bepaalde kansverdeling voldoen worden ook wel ‘stochastische processen’ genoemd.
[3] Wiskundig preciezer: de standaarddeviate groeit als de wortel van het aantal gezette stappen.