
Afbeelding 1. Een kok aan het werk.Aan het eten te zien is dit een goede kok. Maar hoe bepalen we of deze kok de beste is? Foto: Pxhere.
Sommige getallen komen zo vaak in de wis- en natuurkunde voor dat ze een naam hebben gekregen. De bekendste daarvan is waarschijnlijk π, het getal dat de verhouding weergeeft tussen de straal en de omtrek van een cirkel. Om die reden wisten de oude Grieken al dat π onmisbaar is bij haast elke berekening waarin cirkels een rol spelen. Als je als schipper wilt berekenen hoe lang een touw moet zijn dat je een bepaald aantal keer om je mast wilt winden, kun je niet om π heen.
Een ander bekend getal is e, het getal van Euler. In tegenstelling tot π heeft dit getal geen duidelijke meetkundige betekenis. Het getal van Euler komt wel vaak voor in berekeningen die de de grootste kans op een bepaalde uitkomst proberen te vinden. Deze berekeningen zijn vaak een stuk lastiger, en het duurde waarschijnlijk tot de zeventiende eeuw voordat iemand voor het eerst tegen e aanliep. Een mooie manier om een natuurlijke toepassing van e te zien is als volgt.
Stel je voor dat je de hoofdlakei van een strenge doch rechtvaardige koning bent. Op een dag neemt de favoriete kok van de koning ontslag. Als hoofdlakei is het jouw verantwoordelijkheid om de beste vervanger te vinden. Gelukkig heeft zich een grote hoeveelheid kandidaten gemeld. Er is echter maar ruimte voor één kok in de keuken, dus je besluit de kandidaten één voor één een maaltijd te laten koken. Aan de hand van deze maaltijd moet je besluiten of je de kok aanneemt of wegstuurt. Eenmaal weggestuurd zal een afgewezen kok teleurgesteld zijn biezen pakken en nooit meer terugkeren naar het paleis. Hoe kies je nu de beste kandidaat? En hoe groot is de kans dat je die beste kandidaat te pakken krijgt? (Denk voor je verder leest natuurlijk eerst zelf even over het vraagstuk na!)
Het probleem is natuurlijk dat je van tevoren niet weet hoe goed de beste maaltijd zal zijn. Je moet voorkomen dat je de beste kandidaat wegstuurt in de valse hoop dat er nog een betere zal komen. Daarom is het een goed idee om eerst een steekproef te nemen. Laat een aantal kandidaten een maaltijd koken, maar stuur ze allemaal weg. Dit aantal noemen we S. Onthoud de beste van deze S maaltijden, en kies vervolgens de eerste kandidaat die je een betere maaltijd weet voor te schotelen. Mocht er niemand meer komen die een betere maaltijd maakt, dan zit er natuurlijk niets anders op dan de laatste kandidaat aan te nemen.
Deze strategie is natuurlijk niet waterdicht, maar je kunt wel de kans uitrekenen dat je zo de beste kandidaat krijgt. Stel nu dat er in totaal N kandidaten zijn. Hoe groot moet S dan zijn om die kans zo groot mogelijk te maken? Als Euler aan het hof van deze koning had gewerkt, had hij het antwoord geweten. De optimale verhouding tussen S en N is namelijk gegeven door het getal e! Om precies te zijn:
![]()
In woorden: je moet zo’n 37% van de kandidaten testen, voordat je een optimale keuze kan maken. De kans dat je vervolgens de juiste kandidaat kiest, blijkt bovendien ook nog eens gelijk te zijn aan ditzelfde getal: een kleine 37%. Had je verwacht dat die kans zo groot zou zijn?
Dit probleem kan op veel verschillende manieren geformuleerd worden. Voor Valentijnsdag maakte de bekende natuurkundige Carl Bender een filmpje over het vinden van de optimale partner, wat op hetzelfde antwoord uitkomt:
Het wonderbaarlijke van getallen zoals e en π is dat ze in zo veel verschillende problemen tevoorschijn komen. Ze zijn dus niet alleen maar een leuke naam voor een bepaald getal, maar zulke getallen zijn in zekere zin de sleutel tot nieuwe delen van de wiskunde!
Bonus: waarom 1/e?
Misschien is het leuk voor de liefhebbers om een wat meer gedetailleerde berekening van het antwoord te laten zien, aan de hand van deze Wikipedia-pagina. Hoe komen we aan het bovenstaande resultaat? Het staat vast dat één van de N kandidaten de beste is. De kans dat een bepaalde kandidaat, bijvoorbeeld de i-de, de beste kandidaat is komt dus overeen met 1/N.
Stel dat de i-de kandidaat inderdaad de beste is, wat is dan de kans dat deze daadwerkelijk gekozen wordt? Volgens de bovenstaande strategie kunnen we alleen bij deze i-de kandidaat uitkomen als i groter is dan S, de grootte van onze steekproef. Om te zorgen dat de op één na beste kandidaat van alle i-1 voorgaande kandidaten niet per ongeluk in plaats van de beste kandidaat gekozen wordt, is het nodig dat deze tussen de S kandidaten van de steekproef zit. De kans hierop is S / (i-1).
De totale kans dat de i-de kandidaat de beste is én dat deze daadwerkelijk gekozen wordt na een steekproef van S kandidaten is dus
![]()
Zo lang de beste kandidaat maar niet in de steekproef valt, en zo lang deze maar daadwerkelijk gekozen is, maakt het niet uit wat i is. We kunnen de bovenstaande kans dus optellen voor alle i tussen S + 1 en N,
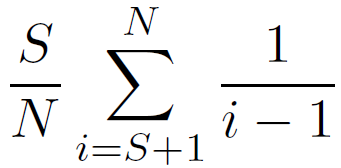
Dit is de totale kans dat deze strategie ons de beste kok oplevert. Voor grote N kunnen we de “-1” in de noemer verwaarlozen, en de bovenstaande som benaderen met een integraal door de variabelen t = i / N en x = S / N in te voeren:
![]()
Wanneer deze kans maximaal is kun je nu gemakkelijk berekenen door de afgeleide te nemen en die op nul te stellen: je vindt dat dat het geval is als x = S/N = 1/e. Bovendien zie je dan (bedenk je dat ln(1/e) = -1) dat de kans zelf ook gelijk is aan die waarde. Zelfs bij een miljoen kandidaten heb je dus nog een redelijke kans om de beste op deze manier eruit te kiezen – een verrassend resultaat!