
Afbeelding 1. Waterdamp op een glasplaat.De overgang tussen vloeibaar water en waterdamp is een van de vele fase-overgangen in de natuur. Afbeelding: rkit.
Op deze website hebben we het al vaak over fasen van materie en de overgangen ertussen gehad. We hebben gezien dat fase-overgangen vaak gepaard gaan met symmetriebreking, bijvoorbeeld bij het vormen van kristallen, waarbij translatiesymmetrie gebroken wordt, of bij een magneet waarin de ferromagnetische ordening vernield wordt als gevolg van een te hoge temperatuur. Bovendien hebben we kennis gemaakt met een heel nieuwe klasse van fasen, namelijk topologische fasen, waar in het bijzonder ook het quantum-Halleffect onder valt, en het verschijnsel van topologische isolatoren.
Deze laatste fasen zijn speciaal, omdat ze niet beschreven worden door de breking van enige symmetrie, maar juist door topologie – eigenschappen die niet veranderen als we een materiaal een klein beetje vervormen. In het artikel over het quantum-Halleffect zagen we bijvoorbeeld dat de geleiding in het ‘integer quantum-Halleffect’ alleen bepaalde discrete waarden kan hebben – iets wat puur en alleen het gevolg van de topologie in het materiaal.
Waarom vinden natuurkundigen al die fasen en de overgangen ertussen zo interessant? En hoeveel fasen van materie bestaan er eigenlijk? In dit artikel zal ik deze vragen nader toelichten.
Landau-theorie
Het antwoord op de eerste vraag is vanuit een natuurkundig perspectief heel vanzelfsprekend: we willen weten hoe de natuur in elkaar zit en dan moeten we begrijpen hoe de natuur zich openbaart in verschillende fasen en waarom dat gebeurt. Om die reden zijn natuurkundigen met allerlei theorietische beschrijvingen op de proppen gekomen om alle fasen in de natuur te kunnen verklaren – en vooralsnog werken de meeste van die theorieën erg goed.
De tweede vraag – welke fasen er bestaan – is een wat abstractere vraag. Daar gaat het om het vergelijken van twee fasen en het proberen te quantificeren wat de verschillen zijn, De onderliggende vraag is natuurlijk: hoe definieer je eigenlijk een fase? Voor fasen zoals bij een opwarmende magneet is het verschil tussen de verschillende toestanden gemakkelijk te meten. In de ferromagnetische fase bij lage temperatuur is er bijvoorbeeld een netto magnetisatie, terwijl bij een te hoge temperatuur, de ferromagnetische ordening verdwijnt en er geen netto magnetisatie meer is – de magneet verliest zijn magneetveld.

Afbeelding 2. Lev Landau.Foto: Nobelstichting.
De magnetisatie is daarom een goede indicator voor de fase waarin een magneet genoemd. Zo’n parameter die je kunt meten om fasen te onderscheiden wordt ook wel een ordeparameter genoemd. In de jaren 30 zetten de Russische natuurkundige Lev Landau een theorie op die ook meer algemene fasen en fase-overgangen kon beschrijven aan de hand van een dergelijke ordeparameter. Deze theorie, tegenwoordig bekend als de Landau-theorie, is een zeer succesvol model dat een groot scala aan fasen en fase-overgangen kan beschrijven.
Er zijn twee fascinerende aspecten aan Landau’s theorie. Ten eerst is het een zeer universeel model, waarvoor geen heel precieze kennis van de fase-overgang nodig is om die te kunnen beschrijven. De enige input in de theorie is wat kennis over de onderliggende symmetriebreking – je hoeft dus eigenlijk alleen te weten welke symmetrie (translatie, rotatie, enzovoort) er gebroken wordt.
Ten tweede, en dat is eigenlijk een gevolg van de eerste opmerking, heb je alleen de ordeparameter nodig om een fase te definiëren. Voor verschillende symmetrieën zijn de gebruikte ordeparameters anders, en dus heb je met een andere fase-overgang te maken. Het bepalen van het aantal fasen is dus niets anders dan het classificeren van de mogelijke ordeparameters!
Toch vangt zelfs Landau’s beschrijving niet alle fasen in de natuur – die theorie gaat alleen over fase-overgangen waarbij de symmetrie van het systeem verandert. Topologische fasen, zoals die in het quantum-Halleffect, vallen niet onder de theorie van Landau en hebben een andere beschrijving nodig. De reden hiervoor is zoals gezegd dat bij topologische fase-overgangen geen symmetrie gebroken wordt – er is dus ook geen ordeparameter. Toch is er een overgang van de ene toestand naar de andere, maar die overgang ontstaat door een verandering in de topologie van het systeem. Hoewel deze fasen niet makkelijk met een ordeparameter geclassificeerd kunnen worden, zijn ze wel op een andere, veel eenvoudigere manier, te classificeren. Dit komt doordat topologische fasen erg robust zijn.
Classificatie van topologische fasen
De eenvoudigste classificatie van topologische fasen is degene die we al een paar keer genoemd hebben: de classificatie van het quantum-Halleffect. De Hall-geleiding blijkt hier gequantiseerd te zijn in stappen, zoals je hier kunt lezen. Dit leidt tot een heleboel fasen want elk stapje brengt het materiaal in een andere fase. Om de fasen van het quantum-Hall effect te classificeren hebben we dus een geheel getal nodig dat het aantal stapjes vanaf een bepaald beginpunt telt. Heel anders dan in de Landau-theorie, dus: geen continu getal (de orde-parameter) dat één mogelijke overgang beschrijft, maar een discreet getal dat heel veel mogelijke overgangen beschrijft.
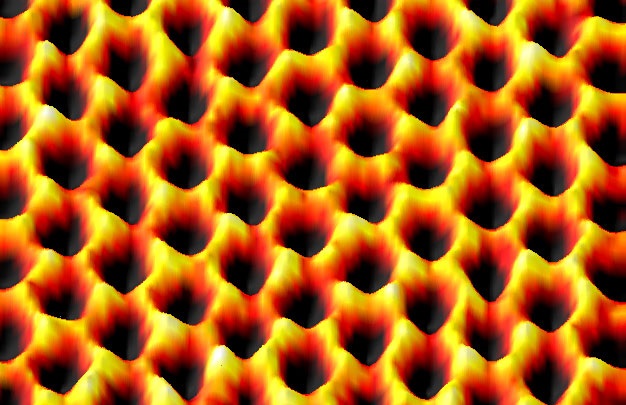
Afbeelding 3. Grafeen.Een afbeelding van grafeen – een materiaal dat het quantum-Halleffect vertoont – gemaakt onder een elektronenmicroscoop. Afbeelding: US Army Materiel Command.
Voor andere topologische fasen zijn er ook bepaalde meetbare grootheden die gequantiseerd zijn, en waar wederom elk stapje correspondeert met een andere topologische fase. Nu lijkt het gebruik van dergelijke grootheden in de praktijk misschien ingewikkelde procedure, want je moet dan telkens de goede meetbare grootheden vinden om te bepalen welke fasen er zijn. Gelukkig is er ook een andere manier. Deze manier maakt echt gebruik van de topologische eigenschappen van een topologische fase. De truc blijkt te zijn om niet een oneindig groot materiaal te bestuderen (iets wat we in de theoretische natuurkunde maar al te vaak doen), maar oom een materiaal van beperkte grootte, en met randen, te onderzoeken. Er zullen in zo’n materiaal deeltjes langs de rand kunnen bewegen, en het mooie is nu: het aantal van zulke deeltjes bepaalt de waarde van de gekwantiseerde grootheid! Je kunt dus ook zeggen dat topologische fasen gedefinieerd en geclassificeerd zijn aan de hand van het aantal deeltjes dat zich op de rand van een materiaal begeeft.
Conclusie
Fasen van materialen zijn er in allerlei soorten en maten. In dit artikel heb ik geprobeerd antwoord te geven op de vraag hoe we fasen en hun overgangen kunnen tellen en classificeren. Voor veel fasen zagen we dat de theorie van Landau voldoende is, maar voor een nieuwere klasse van fasen, de topologische fasen, moest er een nieuwe classificatie ontwikkeld worden, waarbij we naar de rand van het systeem kijken.
Recent zijn onderzoekers, waaronder ikzelf, een stapje verder gegaan in de classificatie van topologische fasen. We hebben topologische isolatoren geclassificeerd aan de hand van de symmetrieen van het kristal waarop ze voorkomen. Hieruit blijkt dat er een heel nieuw scala aan topologische fasen bestaat waar natuurkundigen nog nooit eerder over hadden nagedacht. Ook al is het idee van topologische fasen dus al bijna 40 jaar oud, ze zijn nog langs niet allemaal bekend en geclassificeerd, en blijven ons nog steeds verbazen en fascineren!