
Bij het spelen van een potje biljart probeer je een biljartbal zo te stoten dat deze precies de goede andere ballen op de juiste manier raakt, of in een van de pockets belandt. Voorspellen hoe de bal over de tafel beweegt, is dus cruciaal. Maar niet alleen voor een spelletje biljart is het voorspellen van trajecten relevant: ook natuurkundigen proberen de vraag naar zulke bewegingen te beantwoorden. Nog specifieker stellen ze zichzelf de vraag of de bal ooit een periodieke baan kan volgen. Als de biljartbal nooit zou afremmen1, maakt de bal dan op den duur steeds hetzelfde rondje, of gebeurt dat juist nooit? Het antwoord op die vraag hangt natuurlijk af van de precieze vorm van de biljarttafel. Voor sommige vormen is de vraag makkelijk te beantwoorden, voor andere wat minder.
Een vierkante biljarttafel
Neem als voorbeeld van een ‘makkelijke’ biljarttafel een vierkante. Het is eenvoudig in te zien dat, als je een bal precies loodrecht op een van de randen laat botsen, deze precies hetzelfde pad terug volgt. Ook kun je de bal bijvoorbeeld in een hoek van 45 graden op een van de randen laten botsen. Doordat de hoek van inval gelijk is aan de hoek van terugkaatsing, weten we dat de bal ook onder 45 graden weer van de rand af zal komen. Onafhankelijk van waar de bal op de rand valt, zal de bal na elke rand één keer geraakt te hebben het eigen pad weer volgen.
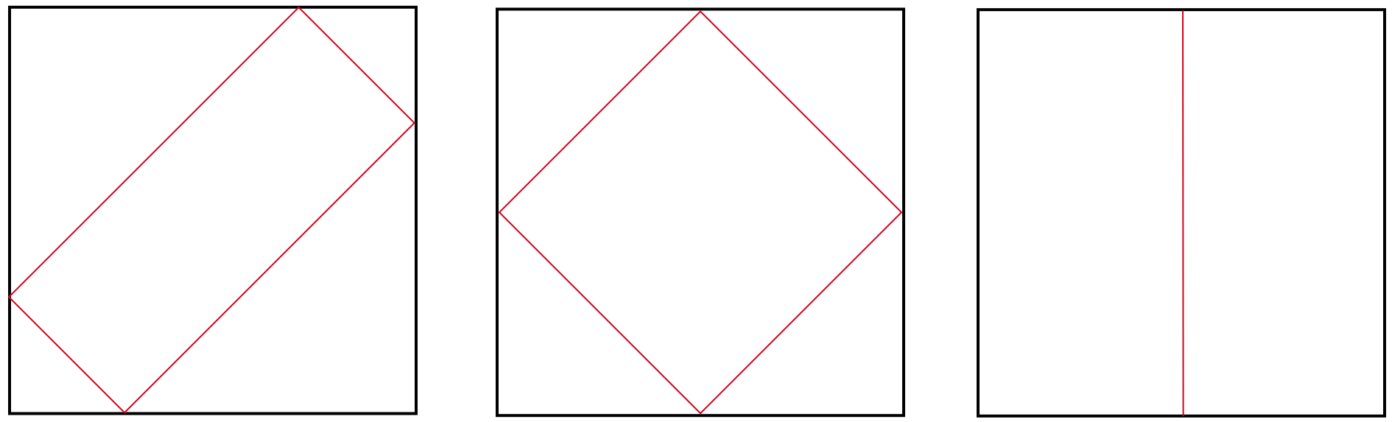
We kunnen vrij eenvoudig een zelfs nog sterkere uitspraak doen. Stel je voor dat we onze biljartbal op een plek met coördinaten \((x_0,y_0)\) neerleggen en deze wegschieten met een snelheid \((v_x,v_y)\). Bij elke botsing met de horizontale rand draait de verticale snelheid om van teken, terwijl bij elke botsing met een verticale rand juist de horizontale snelheid van teken wisselt. Dit betekent dat elke keer dat de biljartbal twee keer de horizontale richting heeft afgelegd, deze zich weer op \(x_0\) bevindt, met horizontale snelheid \(v_x\). Elke keer dat de bal twee keer de verticale richting heeft afgelegd, bevindt deze zich juist weer op \(y_0\) met verticale snelheid \(v_y\). Als het pad van de biljartbal periodiek is, betekent dit dat na een aantal keer botsen deze twee momenten samenvallen. Laten we er voor het gemak van uitgaan dat de tafel precies 1 meter lang en breed is. De bal is heeft dan \( 2n \) keer de horizontale richting afgelegd (dus \( 2n \) meter) in \(2n/v_x\) seconden, en \( 2m \) keer de verticale afstand afgelegd in \(2m/v_y\) seconden. Het pad van de bal is dus periodiek als en alleen als er gehele getallen \( n \) en \( m \) bestaan zodat
\(2n/v_x = 2m/v_y\).
Dit is het geval als \(v_x/v_y\) een rationaal getal is. Het getal \(v_x/v_y\) heet rationaal als er gehele getallen \(p\) en \(q\) bestaan zodat \(p/q=v_x/v_y\). De getallen \(\frac{3}{5}\) (een breuk) en \(10\) (een geheel getal) zijn dus rationale getalen, terwijl bijvoorbeeld \(\sqrt{2}\) en \(\pi\) irrationale getallen zijn. Zolang we de biljartbal op een vierkante tafel onder een rationale hoek wegschieten, zal deze in een periodieke baan terechtkomen. Voor irrationale hoeken herhaalt het pad zich juist nooit.
Een cirkelvormige biljarttafel
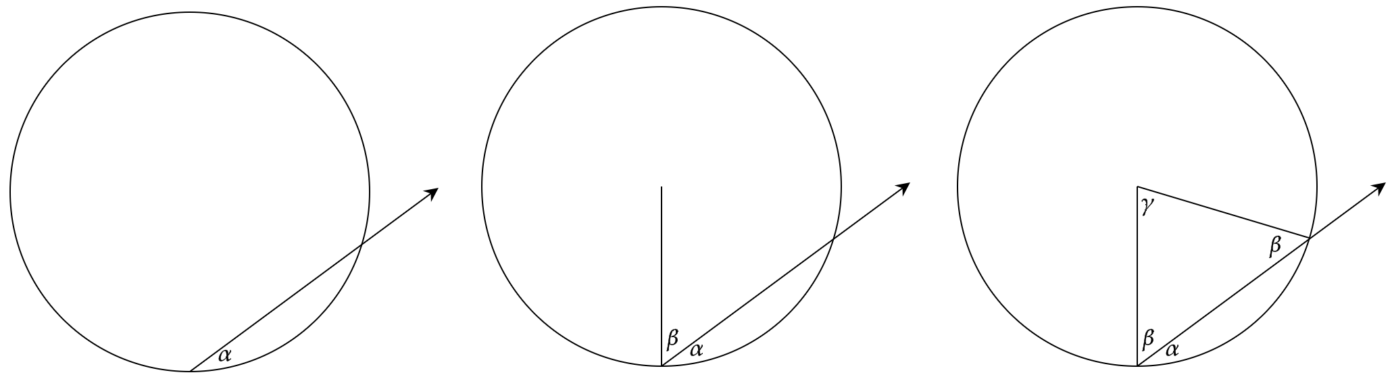
Voor een cirkelvormige biljarttafel is het ook redelijk makkelijk om de banen van de bal te voorspellen. Stel je voor dat je de biljartbal van de rand van de tafel afstoot onder een hoek \(\alpha\). Als we een lijn van het middelpunt van de cirkel naar dit randpunt trekken, maakt de bal een hoek met deze lijn van \(\beta = 90^\circ – \alpha\). Trekken we ook een lijn van het middelpunt naar het punt waar de biljartbal de tafel later weer raakt, dan is die hoek ook \(\beta\). De driehoek die we nu hebben gevormd, heeft in totaal 180 graden, dus de hoek in het midden van de cirkel is \(\gamma=180^\circ – 2\beta = 2\alpha\) graden groot. Dit zal zich na elke botsing zo herhalen. De baan is periodiek als de hoeken in het midden van de cirkel na \(n\) botsingen bij elkaar een veelvoud van 360 graden groot zijn. De hoek in het midden is dus rationaal, en daarmee de hoek \( \alpha \) ook. Alweer is de voorwaarde voor een periodieke baan dat de hoek waaronder je afstoot rationaal is! En omgekeerd: voor irrationale hoeken is de baan niet periodiek.
Driehoekige biljarttafels
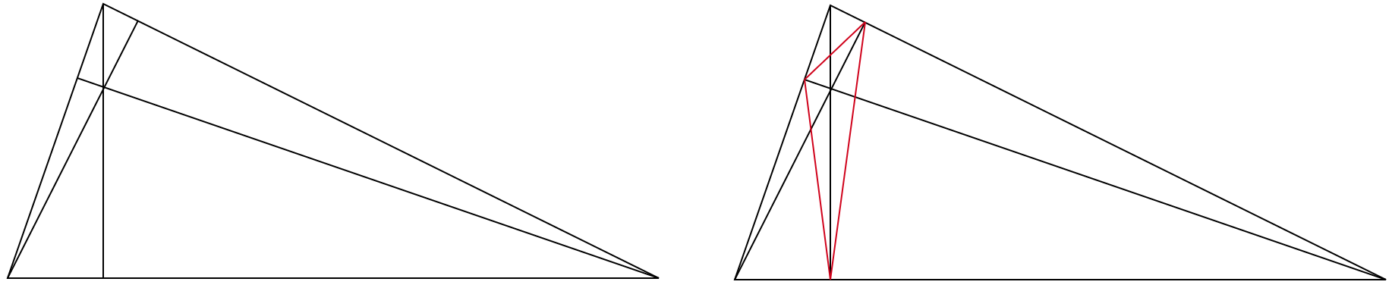
Uit de vorige twee voorbeelden kun je misschien afleiden dat rationale hoeken een grote rol spelen in periodieke banen. Maar er zijn ook biljarttafels waarbij dit niet het geval is! Neem bijvoorbeeld een driehoekige biljarttafel, waarbij alle hoeken minder dan 90 graden groot zijn. Als we vanuit elk hoekpunt een middelloodlijn naar de overstaande zijde trekken, is de driehoek die gevormd wordt door de drie snijpunten met elkaar te verbinden bijvoorbeeld een periodieke baan. Deze constructie werkt zelfs wanneer de hoeken van de originele driehoek irrationaal zijn, en dan zijn de hoeken in de periodieke driehoek ook irrationaal.
Typische banen
We hebben nu voor een paar specifieke vormen van tafels een aantal banen gevonden dat periodiek is, maar ook heel veel banen die dat niet zijn. Maar wat zal een gemiddelde baan zijn, periodiek of niet? Zijn er bijvoorbeeld meer rationale of irrationale hoeken?
Er zijn oneindig veel rationale hoeken te bedenken. Ga maar na, het aantal gehele getallen is oneindig, en rationale getallen zijn opgebouwd uit twee gehele getallen. Je kunt dus concluderen dat er oneindig veel rationale getallen zijn. Het blijkt dat er, hoewel er oneindig veel rationale hoeken zijn, nóg meer irrationale hoeken bestaan. Beide verzamelingen zijn oneindig, maar de rationale hoeken zijn aftelbaar oneindig en de irrationale getallen zijn overaftelbaar oneindig. Aftelbaar oneindig betekent dat je de elementen van de verzameling in een rijtje kunt zetten en dat ze dan allemaal aan de beurt komen. Ook al gaat dat rijtje oneindig lang door, het is een rijtje. Overaftelbare verzamelingen zijn zó groot dat je ze zelfs niet in zo’n rijtje kunt plaatsen. Dit betekent dus dat als je een willekeurige hoek kiest, deze bijna altijd irrationaal is. Het pad van de biljartbal, als we niet heel precies de hoek uitkiezen zodat deze rationaal is, is dus nooit ‘toevallig’ periodiek.
Vlindereffect
Uit het feit dat er meer irrationale dan rationale hoeken zijn, kunnen we al een voorbeeld van het zogeheten ‘vlindereffect’ vinden. Als de biljartbal op een vierkante of ronde tafel precies in een rationale hoek start, is de baan periodiek. Maar als we nu de hoek een héél klein beetje aanpassen, is de baan ineens niet meer periodiek. Hieraan zien we al dat een heel klein verschil in de beginvoorwaardes van de baan een heel groot effect heeft. In het begin zullen de twee ballen die met nét verschillende hoeken starten bovendien ongeveer dezelfde baan volgen, maar al snel beginnen ze verder uit elkaar te gaan en na een tijdje hebben de banen ogenschijnlijk niets meer met elkaar te maken.
Dit verschil is er niet alleen tussen periodieke en niet-periodieke banen. Voor elke beginhoek, rationaal of niet, zullen twee banen met net andere hoeken eerst ongeveer hetzelfde pad volgen, maar al snel ver uit elkaar gaan lopen.
De sterke afhankelijkheid van een systeem van de beginvoorwaarden wordt soms het vlindereffect genoemd. Er wordt vaak gezegd dat de vleugelslag van een vlinder in Brazilië door de minieme luchtstroom die die veroorzaakt, uiteindelijk een orkaan in Texas tot gevolg kan hebben. Dit vlindereffect is een van de kenmerken van chaotische systemen, waar Jeremy van der Heijden eerder al over schreef in dit artikel.
Voorspelbaarheid door chaos
Een ander aspect dat vaak verbonden wordt met chaos, is ergodiciteit, ook benoemd in Jeremy’s artikel. Ergodiciteit betekent dat een systeem de hele ruimte van mogelijke toestanden, de faseruimte uniform verkent. In biljartbaltaal: een biljartbal (in een typische, niet-periodieke baan) komt uiteindelijk op elke plek van de biljarttafel even vaak2. Hoewel de precieze locatie van de biljartbal op de tafel dus heel moeilijk te voorspellen is (onder andere door het vlindereffect), is het door de ergodiciteit juist heel makkelijk andere vragen te beantwoorden. Zo zal de biljartbal ongeveer de helft van de tijd in de linkerhelft van de biljarttafel zijn.
Ook in de natuurkunde, waar heel veel systemen chaotisch zijn, is ergodiciteit een handige eigenschap. Zo is het pad van individuele moleculen in een gas heel moeilijk te volgen: er zijn heel veel moleculen en die botsen ook nog eens continu op elkaar. Maar door de ergodiciteit van dit systeem kun je wel iets zeggen over het gemiddelde van allerlei grootheden, zoals bijvoorbeeld de temperatuur of de druk.
Zo geeft het spelletje biljarten een simpel inkijkje in de wondere wereld van de chaostheorie. Die theorie is nog steeds een heel actief onderwerp in de natuurkunde. Zo kun je er ook op onze site meer over lezen, bijvoorbeeld in de artikelen over zelfmijdende biljartballen, de beweging van sterren rond een zwart gat of zelfs quantumchaos.
[1] We gaan ervan uit dat er geen oneffenheden op de biljarttafel zijn, de randen perfect reflecteren en er geen weerstand is.
[2] De snelheid van de bal is ook onderdeel van de faseruimte. Omdat bij biljarten zonder weerstand de grootte van de snelheid niet verandert verkent de bal dus niet de héle faseruimte, maar wel het hele ‘toegestane deel’ van die ruimte.