
Van snel licht naar traag licht
Stel je voor dat Alice ergens langs een weg staat, en Bob rijdt langs in een auto met een snelheid van 10 meter per seconde. Bob gooit als hij Alice voorbij is vanuit de auto een steentje naar voren, vanuit hem gezien met 3 meter per seconde. Hoe snel ziet Alice dit steentje dan gaan? De klassieke mechanica (en waarschijnlijk je intuïtie) zal je vertellen dat volgens Alice dit steentje een snelheid heeft van 13 meter per seconde: we zijn gewend dat je snelheden bij elkaar kunt optellen. Op deze manier lijkt het echter dat je, als je dit vaak genoeg herhaalt, uiteindelijk een steentje kunt krijgen dat sneller gaat dan het licht. Volgens de speciale relativiteitstheorie kun je snelheden echter niet zomaar bij elkaar optellen. Als we een snelheid \(u\) bij een snelheid \(v\) ‘optellen’ door vanuit een bewegend voorwerp met de ene snelheid een voorwerp met de andere snelheid in dezelfde richting te lanceren, is de nieuwe snelheid volgens die theorie niet \(u+v\), maar
\(\frac{u+v}{1+\frac{uv}{c^2}} \).
In deze formule is \(c\) de lichtsnelheid. Als we nu bijvoorbeeld \(u=0{,}8c\) en \(v=0{,}5c\) bij elkaar optellen, zouden we via onze klassieke optelmethode \(1{,}3c\) krijgen, wat groter is dan de lichtsnelheid. Volgens de relativiteitsformule krijgen we juist \(\frac{1{,}3c}{1{,}4} \approx 0{,}93c\), kleiner dan \(c\)! Zelfs als we de lichtsnelheid bij zichzelf optellen, krijgen we gewoon weer \(c\) terug.
Onze intuïtie voor het optellen van snelheden komt natuurlijk wel ergens vandaan. Voor snelheden die veel kleiner zijn dan de lichtsnelheid, geeft bovenstaande formule bijna hetzelfde antwoord als gewoon optellen. In veel gevallen hoeven we niet de ingewikkeldere formule te bestuderen, maar voldoet het om de ‘niet-relativistische limiet’ te nemen: hierbij doen we in de berekeningen alsof \(c\) oneindig groot is.
Het bovenstaande is allemaal goed bekend en veelgebruikt in de natuurkunde. Het inspireerde Jean-Marc Lévy-Leblond echter om juist de tegenovergestelde, minder begrepen limiet te bestuderen: die waarin we \(c\) ‘oneindig klein maken’. Op het eerste gezicht lijkt deze limiet nergens op te slaan: licht gaat toch juist heel snel, niet heel langzaam? In eerste instantie deed Lévy-Leblond dan ook vooral onderzoek naar dit regime uit wiskundige nieuwsgierigheid. Hij geloofde zelf ook niet dat er veel interesse voor Carrolliaanse natuurkunde zou zijn, dus publiceerde hij zijn artikel in het Frans, in een voor theoretische natuurkundigen relatief onbekend tijdschrift. Toch blijkt de Carrolliaanse limiet, zoals het heet als we \(c\) naar nul sturen, interessant te zijn voor verscheidene natuurkundige onderwerpen.
Deze limiet, Carrolliaanse natuurkunde, is vernoemd naar Lewis Carroll: de auteur van de Alice in Wonderland-boeken. De limiet, waarin licht stilstaat, deed Lévy-Leblond namelijk denken aan een passage in het tweede boek: Through the looking glass. Hierin rennen Alice en de rode koningin heel lang en heel hard, maar ze komen nooit vooruit.
“Well, in our country,” said Alice, still panting a little, “you’d generally get to somewhere else—if you run very fast for a long time, as we’ve been doing.”
“A slow sort of country!” said the Queen. “Now, here, you see, it takes all the running you can do, to keep in the same place. If you want to get somewhere else, you must run at least twice as fast as that!”

De rode koningin vertelt dus aan Alice dat waar ze nu zijn, je zo hard moet rennen als je maar kunt om maar op dezelfde plek te blijven. Als je ergens anders wil komen, moet je minstens twee keer zo hard rennen! Dit lijkt inderdaad op de limiet waarin de lichtsnelheid naar nul gaat. Licht is het allersnelste wat er is, en zelfs met die snelheid kom je in de Carolliaanse limiet niet van je plek af.
Carrolliaanse symmetrie
Een belangrijk aspect van elke natuurkundige theorie wordt gevormd door de symmetrieën die het model heeft. De klassieke wereld zoals wij die zien heeft er ook een paar: translaties (verschuivingen), rotaties (draaiingen) en boosts (het gaan bewegen met een constante snelheid). Samen vormen deze symmetrieën de zogeheten Poincaré-groep. Als er wordt gezegd dat de natuur een Poincaré-symmetrie heeft, wordt er bedoeld dat de natuurkundige formules exact hetzelfde blijven onder zo’n transformatie. Translatie-invariantie betekent dat het niet uitmaakt wáár je een experiment uitvoert: een paar meter naar links of rechts, vooruit of achteruit, boven of onder, een experiment geeft altijd hetzelfde resultaat. Zo is de natuurkunde ook invariant onder translaties in de tijd: een paar uur eerder of later geeft geen andere uitkomst. Ook onder rotaties, draaiingen van je experiment, zou je hetzelfde resultaat moeten krijgen. De laatste symmetrie is wat minder bekend: een Lorentz-boost, waarbij we het experiment met een constante snelheid laten bewegen, mengt ruimte en tijdscoördinaten met elkaar. Wiskundig ziet dat er zo uit:
\( ct’ = \frac{ct-\beta x}{\sqrt{1-\beta^2}}, \quad x’ = \frac{x-\beta ct}{\sqrt{1-\beta^2}}. \)
Hierin is \(\beta\) de snelheid ten opzichte van de lichtsnelheid: \(\beta=v/c\). Wat de bovenstaande formules zeggen is dus: als ik een experiment op een constant bewegend platform zet, en ik meet alles in de nieuwe coördinaten \( t’ \) en \( x’ \), dan vind ik weer dezelfde uitkomsten.
De formule voor de Lorentz-boosts ziet er misschien mysterieus uit, maar vaak worden zulke uitdrukkingen intuïtiever als we de niet-relativistische limiet nemen. Als eerste nemen we aan dat alle snelheden veel kleiner zijn dan die van het licht: \(\beta=v/c \ll 1\). Ook stellen we dat \(x/ct\ll 1\): de afstanden die we bekijken zijn veel kleiner dan de afstanden die het licht kan bereiken. Dan krijgen we de volgende transformatie:
\( ct’ \approx ct(1-\beta x/ct) \approx ct, \quad x’ \approx x(1-\beta ct/x) = x – vt. \)
Let op dat we in de \(x’\)-transformatie \(\beta\) niet kunnen verwaarlozen, omdat \(ct/x\) juist heel groot is. In deze transformatie blijft de tijd zoals je ziet onveranderd – iedereen zal het eens zijn over het tijdstip waarop iets gebeurt – en de \(x\)-coördinaat verschuift met \(vt\): de snelheid keer de tijd. Dit is precies de transformatie die je verwacht tussen als bijvoorbeeld een auto met een snelheid van \(v\) meter per seconde langs een boom rijdt. Volgens iemand die naast de boom staat, blijft die op dezelfde plek \(x=0\). Maar vanuit de auto gezien gaat de boom juist achteruit: na 1 seconde is de boom \(v\) meter achteruit gegaan. De niet-relativistische limiet van de Lorentz-boost is dus een doodgewone Galilei-transformatie!

Nu we iets meer intuïtie voor deze transformatie hebben gekregen, kunnen we ook bijvoorbeeld de Carrolliaanse limiet van de Poincaré-symmetrie bestuderen. We veronderstellen nog steeds dat alles veel langzamer gaat dan het licht: \(\beta = v/c \ll 1 \). Maar in plaats van dat we nu aannemen dat \(x/ct\) heel klein is, stellen we nu dat die verhouding juist heel groot is: \(x/ct \gg 1\). Terwijl we de limiet nemen, ‘zoomen we dus enorm uit’. Dit komt overeen met \(c\) naar nul sturen, in plaats van naar oneindig: we zoomen zo snel uit dat alles stil lijkt te staan. De Lorentz-boost ziet er dan als volgt uit:
\( t’ \approx t(1-\beta x/ct) = t – \beta x/c, \quad x’ \approx x(1-\beta ct/x) \approx x \).
We zien nu dat, in tegenstelling tot de Galileïsche limiet, de tijd juist wel transformeert, en de \(x\)-coördinaat hetzelfde blijft! Dit laatste komt overeen met het idee dat de lichtsnelheid naar nul gaat: als alles langzamer gaat dan het licht, en het licht staat stil, dan staat alles dus stil. Daarin zien we nog maar eens waarom Carroll-natuurkunde vaak het tegenovergestelde van Galileïsche natuurkunde wordt genoemd: de rollen van tijd en ruimte lijken omgekeerd.
We zeggen dat een theorie waarin de resultaten van experimenten niet veranderen onder bovenstaande transformatie, een Carroll-symmetrie heeft. Hoewel in de natuur de lichtsnelheid natuurlijk niet echt nul is, zijn er wel natuurkundige systemen te bedenken waarin de Carroll-symmetrie terugkomt. Zo blijkt dat het hersenspinsel van Lévy-Leblond toch niet puur een wiskundige curiositeit is!
Carrolliaanse holografie
Een voorbeeld van zo’n systeem waarin een Carroll-symmetrie voorkomt is in de holografie. Op deze site zijn al vele artikelen geschreven over holografie, meestal over AdS/CFT. Het idee van het holografische principe nog even kort samenvattend: een theorie van quantumzwaartekracht kan equivalent worden beschreven door een conforme veldentheorie (zonder zwaartekracht) in minder dimensies. Frequente lezers zullen al wel bekend zijn met dit principe, er is al eens een hele serie artikelen over geschreven.
De meest bestudeerde versie van holografie is de al genoemde AdS/CFT-correspondentie. Hierin wordt quantumzwaartekracht in een anti-de Sitterruimte (AdS) in \(d+1\) dimensies ook wel beschreven door een zogeheten conforme veldentheorie (CFT) in \(d\) dimensies. De term ‘anti-de Sitterruimte’ betekent dat de ruimte negatief gekromd is: er is een negatieve kosmologische constante. De anti-de Sitterruimte kan worden voorgesteld als een soort gevuld soepblik; de CFT als het etiket om de soep heen. Beide bevatten dezelfde informatie: wat voor soort soep er in het blik zit.
Ons eigen universum heeft echter geen negatieve kosmologische constante: juist een (heel kleine) positieve! Daarom wordt er ook veel onderzoek gedaan naar andere varianten van de holografie: die voor platte en positief gekromde ruimtes. De meest ontwikkelde variant hiervan is de hemelse holografie (celestial holography), eerder op deze website al beschreven door Boris Post. Hierin wordt bestudeerd of quantumzwaartekracht in een vlakke, vierdimensionale ruimte ook beschreven kan worden door een CFT op de ‘hemelse bol’. Die hemelse bol heeft, zoals Boris al beschreef, twee dimensies. Dat zijn dus twee dimensies minder dan de theorie waarin de quantumzwaartekracht leeft.
Penrose-diagrammen zijn goede manieren om de causale structuren – de wetten van oorzaak en gevolg – in een ruimtetijd te onderzoeken. In zo’n diagram wordt oneindig veel ruimte op een eindig plaatje getekend. De Minkowski-ruimtetijd, de eenvoudigste platte ruimtetijd, is eigenlijk vierdimensionaal, dus in een Penrose-diagram van die ruimtetijd moet je er op elk punt nog een tweedimensionaal boloppervlak bij denken. Licht reist in zulke Penrose-diagrammen altijd onder een hoek van 45 graden. In het Penrose-diagram van de Minkowski-ruimtetijd zie je verschillende soorten oneindig als de buitenste zijden van een ruit. Zo is \(\scr{I}^-\) (de twee onderste zijden van de ruit) het ‘verleden oneindig’: alles is ooit hiervandaan gekomen. \(\scr{I}^+\) (de twee bovenste zijden) is juist ‘toekomstig oneindig’: alles gaat ooit hier eindigen. Dan heb je nog \(i^-\) en \(i^+\), dat zijn de bollen die in het verleden of de toekomst van al het andere liggen. Tot slot is er \(i^0\): dit is ‘oneindig ver weg’ van alles en niets kan dit punt ooit bereiken.
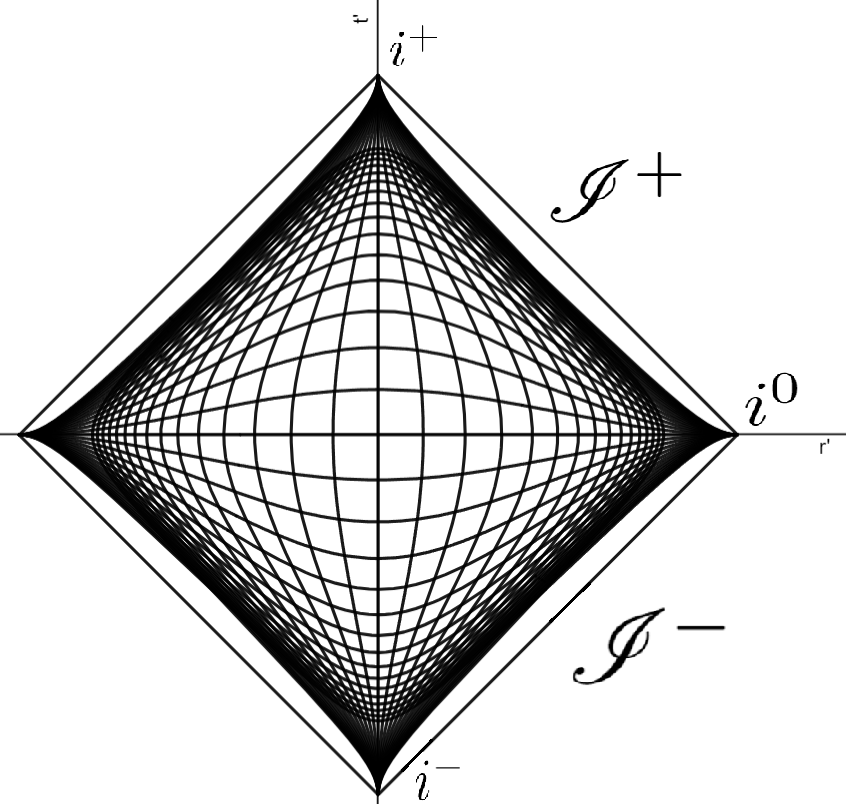
De meest natuurlijke plek om te zoeken naar een theorie op de rand is dus misschien wel \(\scr{I}^+\): toekomstig oneindig. En wat blijkt: er zijn aanwijzingen dat dit inderdaad een conforme veldentheorie is!
Zoals te zien in het Penrose-diagram ligt \(\scr{I}^+\) in het diagram precies onder een hoek van 45 graden. Dit geeft al aan dat er hier iets geks aan de hand is als we nadenken over causaliteit: alleen het licht lijkt twee punten op zo’n zijde te kunnen verbinden. Als de symmetrieën van \(\scr{I}^+\) worden bestudeerd, blijkt dat er daar een Carroll-symmetrie is: de theorie is daar invariant onder de Carroll-transformatie. In onze zoektocht om vlakke ruimte holografisch te beschrijven, zijn we gestuit op een theorie die eerst alleen voortkwam uit de nieuwsgierigheid van de Franse natuurkundige Lévy-Leblond!
Er is nog veel verwarrend is aan Carrolliaanse natuurkunde. Daarom bestuderen wetenschappers vaak een net andere theorie: ze verwijderen (door integreren over \(\scr{I}^+\)) twee van de coördinaten, en houden een CFT in twee dimensies over: die op de hemelse bol! Dat is de basis van het onderzoek dat hemelse holografie wordt genoemd.
Er is ook nog een groep wetenschappers die de driedimensionale, Carrolliaanse holografie bestudeert. In AdS/CFT ‘leeft’ de CFT ook één dimensie lager dan de quantumzwaartekracht, en AdS/CFT wordt wél heel goed begrepen. Daarom hopen zij dat door de Carrolliaanse natuurkunde in drie dimensies beter te begrijpen, ons begrip over het holografisch principe in vlakke ruimtes ook dichterbij komt.
Er valt op het gebied van Carrolliaanse natuurkunde nog heel wat te ontdeken, en je kunt er zoals je ziet allerlei kanten mee op. Zoals Lewis Carroll het zelf formuleerde:
Curiouser and curiouser…