Afbeelding 1. Robert Brown (1773 – 1858)Foto: Maull & Polyblank.
Brownse beweging
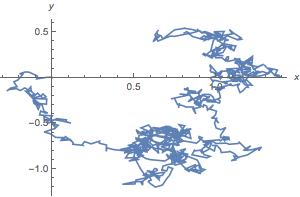
Om de theorie van Einstein goed te begrijpen, moeten we eerst het verschijnsel zelf iets beter toelichten. Laten we daarom eens stofdeeltjes in de lucht bestuderen, bijvoorbeeld als er toevallig een zonnestraal door het raam naar binnenvalt, zodat de stofdeeltjes het licht reflecteren en je ze goed kunt zien. In dat geval zul je ontdekken dat de stofdeeltjes niet alleen maar naar beneden bewegen als gevolg van de zwaartekracht, maar dat ze eigenlijk vrijwel willekeurig door de lucht bewegen. Bovendien bewegen ze snel en verandert hun richting relatief snel. Die laatste observatie is belangrijk, want het betekent dat de stofdeeltjes vele botsingen aangaan met de andere hoofdrolspeler: de luchtmoleculen. Deze willekeurige beweging van de stofdeeltjes noemen we ook wel de Brownse beweging. Brownse bewegingen komen niet alleen voor bij stofdeeltjes in de lucht, maar ook bij kleine deeltjes opgelost in water of eiwitten in onze cellen. In de afbeelding hieronder zie je een simulatie van een Brownse beweging.
Afbeelding 2. Brownse beweging.Een simultatie van een Brownse beweging. Het stofdeeltje begint in de oorsprong en botst zo nu en dan met de luchtmoleculen, zoals je kunt zien aan de scherpe veranderingen van de richting van het stofdeeltje.
Einsteins aanpak
Door die vele botsingen is het praktisch onmogelijk om, zoals in andere mechanische problemen gebeurt, exacte krachtenbalansen op te stellen en de beweging van het stofdeeltje via de wetten van Newton uit te rekenen. Gelukkig kun je wel, mede dankzij de willekeur van de beweging, een statistische benadering gebruiken waarin je alleen geinteresseerd bent in gemiddelde waarden van bepaalde fyische grootheden.
Dit is dezelde aanpak als die in de theormodynamica wordt gebruikt. We zijn ook daar niet geinteresseerd in the beweging van een afzonderlijk atoom of molecuul, maar in gemiddelde grootheden zoals temperatuur, energie en entropie. Voor de situatie met stofdeeltjes willen we kijken naar hun dichtheid om daaruit later de gemiddelde verplaatsing van het stofdeeltje af te leiden. De dichtheid is een functie van zowel tijd als positie, want de stofdeeltjes kunnen op verschillende plekken in de lucht zitten en hebben ook een snelheid.
Einstein liet zien dat de dichtheid van stofdeeltjes door de invloed van de botsingen voldoet aan een speciale en mooie vergelijking in de natuurkunde: de diffusievergelijking. De diffusievergelijking vertelt je eigenlijk wat de naam al zegt: hoeveel de dichtheid van stofdeeltjes in de lop van de tijd uitgespreidt over de ruimte. De gemiddelde snelheid van die uitspreiding noemen we de diffusieconstante, D. Het lukte Einstein om niet alleen te laten zien dat de stofdichtheid aan deze vergelijking voldoet, hij kon ook de waarde van de diffusieconstante D relateren aan aandere meetbare grootheden. Zo liet hij zien dat het gemiddelde van het kwadraat van de verplaatsing van het stofdeeltje gelijk is aan twee maal de diffusieconstante maal de tijd, oftewel
![]()
Kortom, de gemiddelde verplaatsing van stofdeeltjes gaat niet linear, zoals de verplaatsing van een auto die met constante snelheid rijdt, maar met de wortel van de tijd!

Afbeelding 3. Stof in de zon.Stofdeeltjes in de zon geven niet alleen een mooi schouwspel, ze gedragen zich ook volgens interessante onderliggende natuurkunde! Foto: wikipedia-gebruiker E.mil.mil.
De Einsteinrelatie
In het begin van dit artikel beweerde ik dat we met de theorie van Einstien ook indirect bewijs kregen voor het bestaan van atomen en moleculen. Dat werkt als volgt. Om te beginnen kan er een afleiding gegeven worden van een relatie tussen de diffusieconstante en thermodynamische grootheden van de omgeving, zoals bijvoorbeeld de temperatuur van de lucht. Die relatie wordt gegeven door
![]()
Hier is R de gasconstante, T de temperatuur van de lucht, η de viscositeit van de lucht, r de straal van het stofdeeltje en N het getal van Avogadro, een getal dat aangeeft hoeveel moleculen of atomen er zitten in een bepaalde hoeveelheid materie – bijvoorbeeld in zo’n 28 gram stikstofmoleculen, het belangrijkste ingrediënt van lucht. De diffusieconstante is volgens Einsteins theorie zoals we zagen gerelateerd aan het gemiddelde van het kwadraat van de afstand die de stofdeeltjes afleggen, en de overige variabelen zijn gemakkelijk te bepalen, behalve N. Je kunt met dit experiment dus N bepalen, en de waarde vergelijken tussen verschillende experimenten om te zien of daar inderdaad een constante waarde uit komt. Zo weet je ook hoeveel massa elk atoom of molecuul moet hebben, en dus heb je indirect bewijs geleverd voor het bestaan van moleculen en atomen!
Natuurlijk weten we tegenwoordig ook dat atomen en moleculen bestaan door ze onder een zeer speciale microscoop te bekijken, maar destijds was het nog helemaal niet zo duidelijk waar alle materie uit opgebouwd was. De theorie van Einstein bracht een grotere zekerheid met zich mee dat atomen en moleculen echt bestaan en was voor veel wetenschappers het begin van een nieuw tijdperk waarin er dieper werd nagedacht over het allerkleinste. Iets waar we nu, meer dan honderd jaar later, nog steeds druk mee bezig zijn – en waarschijnlijk ook nog wel even zoet mee zullen zijn.