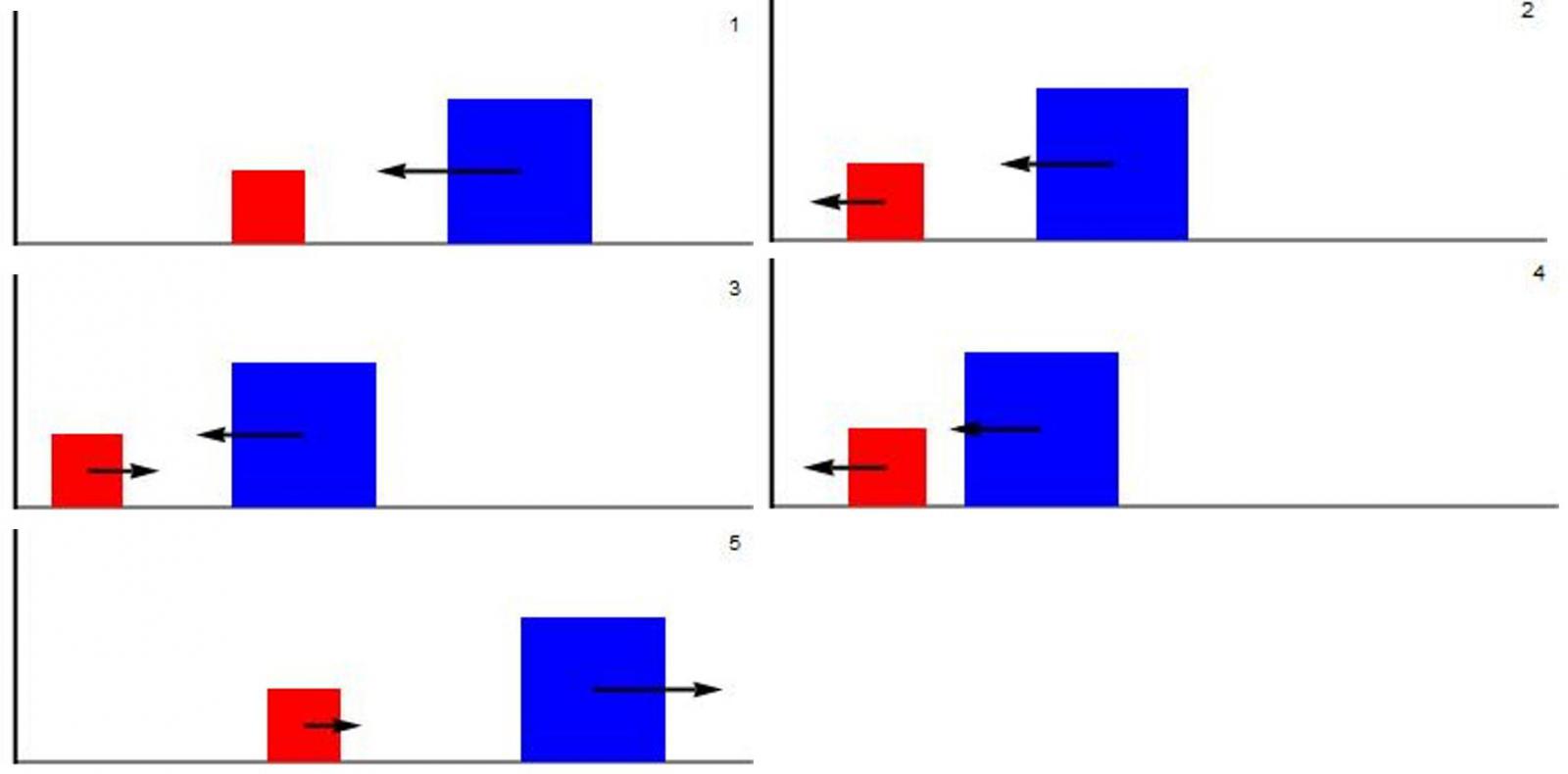
Afbeelding 1. Botsende blokken.Het blauwe, zware blok botst diverse malen met het rode, lichte blok, dat op zijn beurt steeds tegen de muur botst en omkeert.
Opstelling
We nemen twee blokken en een muur. Blok 2 ligt stil tussen de muur en blok 1 in, terwijl blok 1 richting de muur en blok 2 beweegt (afbeelding 1.1). Vervolgens botsen de blokken, waardoor blok 2 nu ook richting de muur beweegt (afbeelding 1.2). Blok 2 wordt op een gegeven moment door de muur teruggekaatst (afbeelding 1.3), wat betekent dat de blokken opnieuw kunnen botsen (afbeelding 1.4). Dit proces blijft zich herhalen, totdat blok 1 zo snel van de muur weg beweegt dat het als het ware ontsnapt aan blok 2 (afbeelding 1.5).
Het idee van deze puzzel (die we vonden op het kanaal 3Blue1Brown op Youtube) is dat, als je het aantal botsingen tussen deze twee blokken telt, je uiteindelijke antwoord een benadering van het getal π is. Hierbij moet de massa van blok 1 wel precies een even macht van 10 groter zijn dan de massa van blok 2, oftewel m1 = 102d m2, en het aantal correcte decimalen wordt dan gegeven door d+1. Als we bijvoorbeeld d=1 kiezen, dus blok 1 honderd keer zo zwaar maken als blok 2, tellen we 31 botsingen. Voor d=2 tellen we 314 botsingen, enzovoort. Let wel: in de praktijk werkt het experiment alleen als er geen energie verloren gaat door wrijving, dus hoge waarden van d zijn eigenlijk alleen op papier bereikbaar. Dat neemt natuurlijk niet weg dat het resultaat zeer verrassend is. Om dit gedrag te kunnen verklaren, hebben we meerdere feiten uit de mechanica en de meetkunde nodig.
Behoudswetten
De bekendste behoudswet in de natuurkunde is waarschijnlijk de wet van behoud van energie. Deze wet vertelt ons dat, wat er ook gebeurt, de totale energie in een systeemaltijd gelijk zal blijven. De enige soort energie die in onze puzzel voorkomt, is de kinetische energie van de blokken (ook wel bewegingsenergie genoemd), gegeven door
![]()
In deze vergelijking zijn m1, m2 de massa’s van de blokken, en v1, v2 de snelheden ervan. Omdat deze energie constant moet blijven, vertelt de wet van behoud van energie ons welke waarden de snelheden v1, v2 kunnen aannemen. Op het eerste oog lijkt deze informatie nog niet heel erg nuttig. Maar als we
![]()
als coördinaten in het tweedimensionale vlak interpreteren, vertelt het ons dat we alleen punten kunnen vinden op de cirkel met straal R = √E. De wet van behoud van energie kan dan namelijk herschreven worden tot R2 = x2 + y2, de vergelijking voor een cirkel. Onze beginsituatie, waarin v2=0, komt dan overeen met het linkeruiteinde van de cirkel.
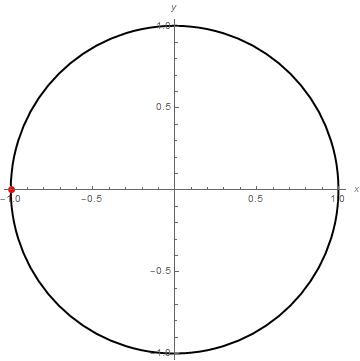
Afbeelding 2. Behoud van energie als een cirkel.We hebben hier voor het gemak R=1 gekozen. De rode punt geeft de beginsituatie van het experiment aan.
De andere behoudswet die we kunnen gebruiken is de wet van behoud van impuls. Ter herinnering: de impuls van een blok is zijn snelheid vermenigvuldigd met zijn massa. Deze wet vertelt ons dat de som van de impulsen van de blokken vóór de botsing gelijk moet zijn aan de som van de impulsen ná de botsing. Deze behouden totale impuls is in een formule dus gegeven door
ptotaal = m1 v1 + m2 v2
Zoals de wet van behoud van energie als een cirkel kon worden getekend, kan deze wet als een lijn worden getekend. Door onze analyse voor de cirkel weten we al dat deze lijn het linkeruiteinde van de cirkel moet snijden, aangezien dat met onze beginsituatie overeenkomt. En als we opnieuw de coördinaten x, y gebruiken, kunnen we de richtingscoëfficiënt van de lijn, −√(m1/m2), uit de behoudswet aflezen. Hiermee kunnen we deze lijn doortrekken, en dan vinden we dat de lijn de cirkel in nog één ander punt snijdt. Dit tweede punt (zie afbeelding 3 hieronder) vertelt ons wat de snelheden van de blokken na de botsing zijn.
Hierna komt de botsing van blok 2 met de muur. De grootte van de snelheid van het blok blijft gelijk, alleen de richting van het blok verandert. Dit kunnen we opvatten als een verticale lijn in ons plaatje. Het veranderen van richting komt namelijk overeen met v2 door −v2 vervangen, waarbij y dus −y wordt.
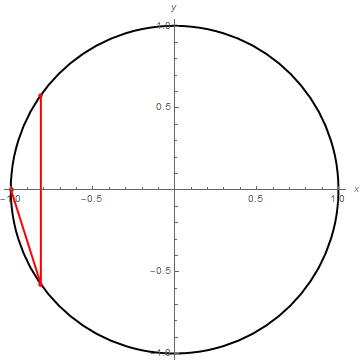
Afbeelding 3. De eerste twee botsingen.De rode lijnen geven aan hoe de snelheden van de blokken tijdens de botsingen veranderen.
Dit trucje kunnen we blijven herhalen, totdat we bij het rechter uiteinde van de cirkel uitkomen. Hierna is blok 1, zoals al werd voorspeld, ontsnapt aan blok 2, omdat het met een hogere snelheid dan die van blok 2 van de muur weg beweegt. Zie hieronder enkele voorbeelden:
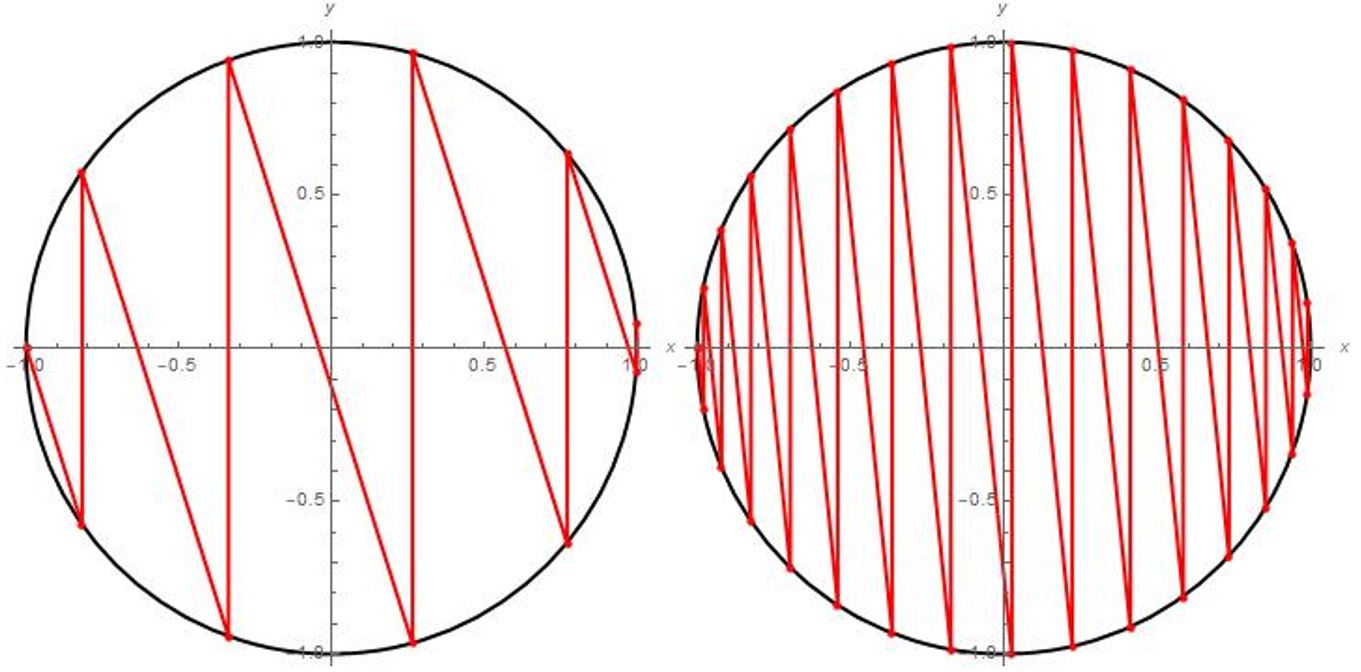
Afbeelding 4. Het hele proces.Twee voorbeelden van het hele botsingsproces met verschillende waarden van m1 en m2.
Tot π tellen
Onderhand begrijpen we onze puzzel toch al wel redelijk goed, maar hoewel er een cirkel in ons verhaal voorkomt lijken we tegelijkertijd nog niet veel dichter bij het benaderen van π. Het idee was immers dat het tellen van het aantal botsingen van de blokken de decimalen van π zou opleveren. In onze plaatjes komt het aantal botsingen tussen de blokken overeen met het aantal diagonale lijnen, maar er is ook een andere manier waarop we dit aantal kunnen tellen. Alle punten op de cirkel delen de cirkel namelijk op in bogen (de meest rechter boog uitgezonderd). En dit aantal bogen is gelijk aan tweemaal het aantal botsingen. Om deze bogen nu aan te kunnen relateren, hebben we een paar trucjes met hoeken nodig.
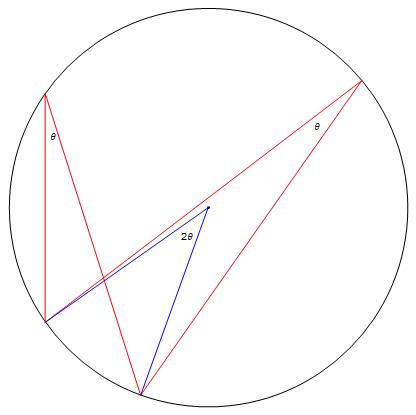
Afbeelding 5. Omtrekshoek en middelpuntshoek.Een middelpuntshoek (blauw) en twee bijbehorende omtrekshoeken (rood). De twee rode hoeken zijn even groot!
De eerste truc heeft te maken met zogenaamde omtrekshoeken en middelpuntshoeken. De omtrekshoek is de hoek die wordt gevormd door twee lijnen vanaf de uiteinden van een boog te trekken naar een ander punt op de cirkel. De hoek die deze lijnen in dit punt maken wordt de omtrekshoek genoemd. Het blijkt dat het niet uitmaakt voor de hoek waar we dit punt op de cirkel plaatsen, want de hoek blijft altijd hetzelfde (de omtrekshoekstelling). We kunnen ook lijnen naar het middelpunt van de cirkel trekken vanaf de uiteinden van de boog. Dit wordt de middelpuntshoek genoemd. Deze hoek blijkt altijd tweemaal zo groot als de omtrekshoek te zijn.
Nu gaan we deze truc toepassen. Laten we beginnen bij de middelpuntshoek die hoort bij een van de bogen, en zeggen dat deze hoek grootte 2θ heeft. Dan valt ons op dat iedere boog ook een specifieke omtrekshoek heeft. Namelijk, de hoek tussen de verticale lijn en de horizontale lijn. Met behulp van de truc hierboven weten we dat deze hoek grootte θ heeft. En aangezien de verticale lijn en de horizontale lijn elkaar altijd onder dezelfde hoek snijden, hoort dus bij iedere boog dezelfde middelpuntshoek 2θ. Dus de boogjes die we getekend hebben zijn allemaal even groot, en delen 2π op in gelijke stukjes van 2θ. Als er N botsingen hebben plaatsgevonden, betekent dit dus dat we 2π van onderen benaderen met 2Nθ. De fout in deze benadering is het kleine stukje boog aan de rechterkant dat nog overbleef.
Nu rest ons alleen nog het berekenen van de hoek θ. Met behulp van een beetje trigonometrie vinden we als volgt dat tan(θ) = √(m1/m2). Hierbij gebruiken we dat de aanliggende zijde (horizontaal) lengte 1 heeft als de overstaande lijn (verticaal) lengte √(m1/m2) heeft. Dit kunnen we beredeneren uit de richtigscoefficient van de diagonale lijn die volgde uit het behoud van impuls. Ten slotte gebruiken we dat de tangens van een hoek de lengte van de overstaande zijde gedeeld door de lengte van de aanliggende zijde is (volgens het beroemde ezelsbruggetje: SOS, CAS, TOA). Voor kleine hoeken die we in radialen meten, weten we bovendien dat tan(θ) ≈ θ. Dus in deze benadering vinden we dat θ ≈ √(m1/m2). Kies nu m1 = 102d m2, en je vindt dat π door 10d N van onderen wordt benaderd. Oftewel: N benadert tot op d decimalen nauwkeurig π!
Het bovenstaande bewijs is beslist niet eenvoudig, maar toont wel een heel interessante wisseling van perspectief. We blijken een natuurkundig probleem uit de mechanica te kunnen herformuleren als een wiskundig probleem in de meetkunde, en dat vervolgens te kunnen oplossen. Dit voorbeeld staat overigens niet op zich: meetkunde blijkt op allerlei verrassende plaatsen in de natuurkunde steeds weer terug te komen – denk bijvoorbeeld aan hoe Albert Einstein met zijn relativiteitstheorie ook zwaartekracht als meetkunde beschreef. We leven in een verbazend meetkundige wereld!
Referenties
We vonden deze puzzel op https://www.youtube.com/watch?v=HEfHFsfGXjs en de oplossing op https://www.youtube.com/watch?v=jsYwFizhncE, beide op het kanaal 3Blue1Brown op YouTube.
Afbeelding voorpagina: Alicja (Pixabay).