
Zwart en wit
Om te begrijpen of witte gaten (kunnen) bestaan, moet ik eerst uitleggen wat we daarmee bedoelen. Zwarte gaten zijn zo zwaar, dat niets eraan kan ontsnappen, zelfs licht niet. Omdat ze geen enkel licht uitstralen, zullen we ze nooit zien: daarom noemen we ze zwart. Een logische definitie voor een wit gat zou dan bijvoorbeeld kunnen zijn: een object waar alles onherroepelijk uit verdwijnt. Kan zoiets echt bestaan?
Het klinkt allemaal nogal vreemd, maar op het eerste gezicht was ook het idee van zwarte gaten voor veel mensen onvoorstelbaar! Zwarte gaten kwamen als oplossing uit de Einsteinvergelijkingen rollen, maar zelfs Einstein geloofde er niet in. Zelf publiceerde hij ook een artikel waarin hij concludeerde dat zwarte gaten nooit in onze echte wereld konden bestaan. Maar intussen wordt het bestaan van zwarte gaten niet meer betwist: in 2019 is er voor het eerst één direct gefotografeerd!
Om iets te kunnen zeggen over het eventuele bestaan van witte gaten, moeten we eerst wat dieper in de wiskunde achter zwarte gaten duiken: dezelfde wiskunde voorspelde immers ook het bestaan van zwarte gaten, ver voordat we er zelf echt van overtuigd waren dat ze bestonden. De komende alinea’s zijn dus iets aan de technische kant, maar wat mij betreft onvermijdelijk om te begrijpen hoe witte gaten (spoiler alert!) als oplossing van de Einsteinvergelijkingen gevonden zijn. En dan resteert altijd nog de vraag: bestaan witte gaten ook in het echt?
De wiskunde van zwarte gaten
Eerst dus wat meer over zwarte (en witte) gaten en hun wiskundige beschrijving. Iedere oplossing van de Einsteinvergelijkingen kan beschreven worden aan de hand van een zogeheten metriek. Dat is een beschrijving van de ruimtetijd, het geheel van ruimte en tijd, en de bijbehorende kromming op elk punt. Platte ruimte, waarin geen enkele massa en dus geen zwaartekracht aanwezig is, wordt beschreven met de Minkowski-metriek:
\( \mathrm{d}s^2 = -\mathrm{d}t^2 + \mathrm{d}x^2 + \mathrm{d}y ^2 + \mathrm{d}z^2 \).
In deze formule is \( t \) de tijd, en \( x, y \) en \(z\) zijn de drie ruimtecoördinaten die we in de wereld om ons heen zien. Het is niet heel belangrijk om precies te begrijpen wat hierboven staat, maar ik zal de belangrijkste aspecten kort toelichten. De getallen vóór de coördinaten – in dit geval zijn die steeds +1 of -1 – beschrijven de kromming. In de Minkowski-metriek hangen die getallen zélf niet van de coördinaten af; ze zijn overal constant, wat aangeeft dat er geen zwaartekracht wordt gevoeld in een ruimte zonder massa. Ook belangrijk is dat het getal -1 voor het tijdgedeelte – de \( \mathrm{d} t^2 \) – negatief is, terwijl de getallen +1 voor de ruimtecoördinaten positief zijn. Dit weerspiegelt het feit dat de tijd een fundamenteel andere rol speelt in de algemene relativiteitstheorie dan de ruimte. Ga maar na: wij ervaren de wereld om ons heen als een driedimensionale wereld, waarin tijd een wezenlijk andere rol vervult.
Goed, élke oplossing van de algemene relativiteitstheorie, niet alleen de vlakke ruimtetijd, kan dus worden opgeschreven in zo’n soort metriek. Al vlak na Einsteins publicatie van deze zwaartekrachtstheorie kwam Karl Schwarzschild met een merkwaardige oplossing van die Einsteinvergelijkingen: de Schwarzschildmetriek. Deze metriek beschrijft een ruimtetijd met een punt met massa \( M \) in het midden, en ziet er als volgt uit:
\( \mathrm{d}s^2 = – \left(1-\frac{2M}{r}\right)\mathrm{d}t^2 + \frac{\mathrm{d}x^2}{1 -\frac{2M}{r} } + r^2 \left(\mathrm{d}\theta^2 + \sin^2 \theta \mathrm{d}\phi^2\right) \).
Hier is \( t \) weer de tijdscoördinaat en \( r \) is de afstand tot de puntmassa. De andere twee ruimtecoördinaten, \( \theta \) en \( \phi \), zijn twee hoeken, onbelangrijk voor het verdere verhaal. Oneindig ver van het midden, dus als \( r \) heel groot wordt, blijkt deze uitdrukking de Minkowski-metriek zonder massa te benaderen, maar dan omgeschreven in het coördinatenstelsel \( (t,r, \theta, \phi) \). Dit is in overeenstemming met het feit dat heel ver van een massa de zwaartekracht nauwelijks effect meer heeft, en dat daar de beschrijving van de ruimtetijd dus moet lijken op de Minkowski-metriek.

Als we nu echter langzaam dichter bij de puntmassa komen, wordt de kromming sterker en merken we meer van de zwaartekracht. En niet alleen wordt de zwaartekracht sterker: er zijn twee waardes van \( r \) waarop de kromming in deze coördinaten iets geks doet. De eerste is het midden, op de plek van de puntmassa, \( r=0 \). In de metriek staat de breuk \( \frac{2M}{r} \), en bij \( r=0 \) moeten we dus delen door nul: de kromming wordt oneindig! Dit heeft te maken met het feit dat je in de echte wereld natuurlijk niet oneindig veel massa op een oneindig klein punt kunt samenproppen. Op kleine afstanden beginnen quantumeffecten bijvoorbeeld een rol te spelen, en daar houdt algemene relativiteit nu net geen rekening mee. Om dit middelpunt goed te kunnen beschrijven, hebben we dus eigenlijk een theorie van quantumzwaartekracht nodig, maar daar zijn natuurkundigen nog niet over uit. Voor nu accepteren we de oneindige kromming in het centrum van deze ruimtetijd, die we overigens de singulariteit noemen.
Maar er is nóg een bijzonder punt: \( r=2M \). Deze afstand \( r \) wordt ook wel de Schwarzschildstraal of de horizon genoemd. Ook hier vinden we nullen en oneindigheden in de Schwarzschildmetriek. En er is nog iets geks: voor punten binnen deze horizon, met \( r<2M \), wisselt het teken voor de tijds- en afstandscoördinaten om. Het getal voor \( \mathrm{d}t^2 \) is nu positief, terwijl dat voor \( \mathrm{d}r^2 \) juist negatief is geworden. Zoals we eerder al zagen in de Minkowski-metriek, weerspiegelt dit negatieve teken de rol van de tijd. Binnenin de horizon draaien de rol van afstand en tijd dus om!
Met de technieken van de algemene relativiteit kan overigens de daadwerkelijke kromming van de ruimtetijd op deze horizon worden berekend: die blijkt helemaal niet echt oneindig te zijn. Dat de kromming oneindig lijkt op de Schwarzschildstraal, is een bijkomstigheid van de coördinaten die Schwarzschild heeft gekozen. Maar dit betekent niet dat er alsnog niets geks aan de hand is. De ruimtetijd die Schwarzschild beschrijft met zijn metriek, is namelijk een bijzondere: de metriek beschrijft een zwart gat!
Een slimme weergave
Om dat in te zien, is het handig om te kijken naar zogenoemde Penrose-diagrammen. Dit zijn een soort tijd-ruimtediagrammen (al eerder besproken op deze site) waarin oneindige ruimte in een eindig plaatje wordt weergegeven. De belangrijkste regels voor het interpreteren van zo’n diagram zijn als volgt:
- Licht reist langs lijnen onder een hoek van 45 graden.
- Alles met massa (een planeet, een appel of een astronaut met een raket) reist langs lijnen die steiler zijn dan 45 graden.
De metriek van Schwarzschild heeft het volgende bijbehorende Penrose-diagram:
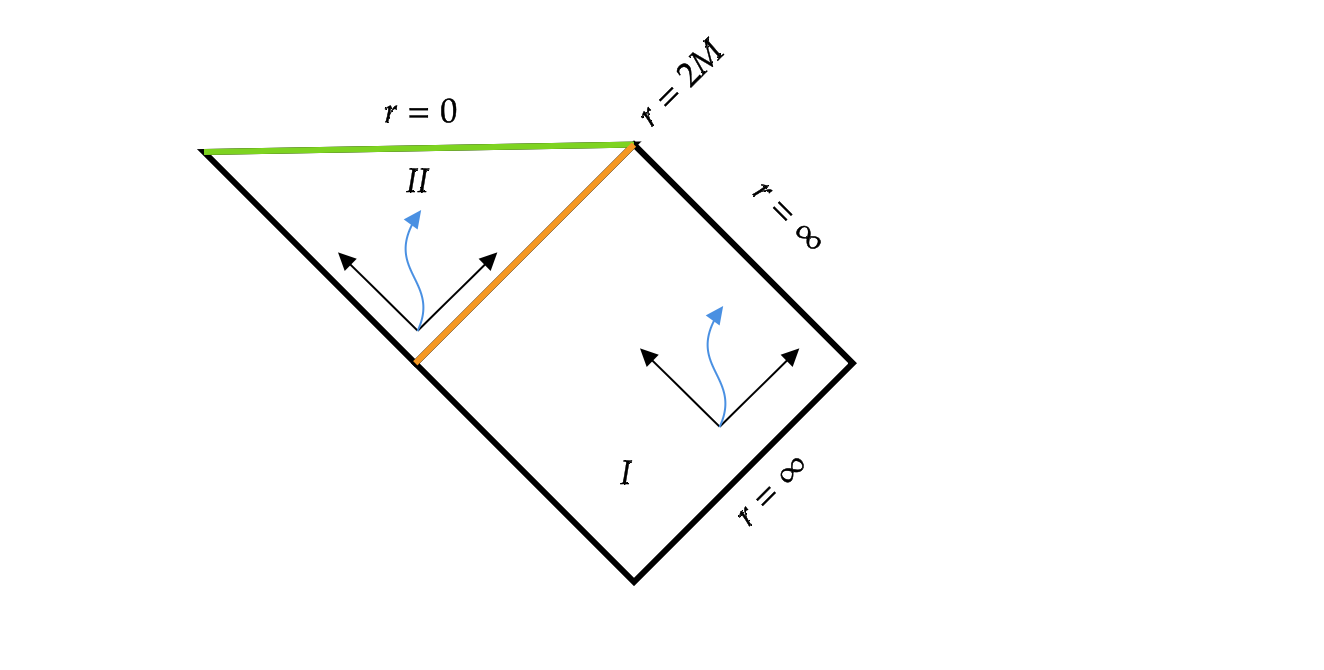
De groene lijn is de singulariteit op afstand \( r=0 \), en de oranje lijn is de horizon. Gebied I is de ruimte buiten de horizon, gebied II de ruimte binnenin. De zwarte pijlen, onder hoeken van 45 graden, geven (delen van) mogelijke paden van lichtstralen weer, terwijl de steilere blauwe gekromde lijnen voorbeelden zijn van hoe bijvoorbeeld een astronaut met een raket zou kunnen bewegen.
Het ‘lezen’ van een Penrose-diagram is iets waar je even aan moet wennen; je zou niet direct gokken dat het bovenstaande plaatje een vervormde weergave van een zwart gat is! Toch is vanuit dit plaatje bijvoorbeeld goed te zien hoe, eenmaal binnenin de horizon, in gebied II, niets meer naar buiten kan komen. Zelfs de minst steile lijnen, de lichtstralen, komen nooit meer voorbij de oranje lijn. Alles wat en iedereen die binnen de horizon is gekomen, komt bovendien onvermijdelijk terecht op de groene lijn, de singulariteit. Iets anders geldt voor waarnemers in gebied I. Afhankelijk van het genomen pad, kom je daar óf terecht op de singulariteit, of veilig daarbuiten[1], op \( r=\infty \).
Vanuit dit Penrose-diagram is dus op te maken dat de Schwarzschildmetriek inderdaad een zwart gat beschrijft: een object waaruit niets meer kan ontsnappen! Gebied I beschrijft de wereld buiten het zwarte gat, en gebied II de ruimtetijd daarbinnen.
Een ander eigenaardig kenmerk van zwarte gaten waar je misschien ooit van hebt gehoord: als jij iemand in een zwart gat ziet vallen, ziet het er net uit alsof dat steeds langzamer en langzamer gebeurt. Is dat ook te zien vanuit het Penrose-diagram? Kijk even mee naar afbeelding 4.
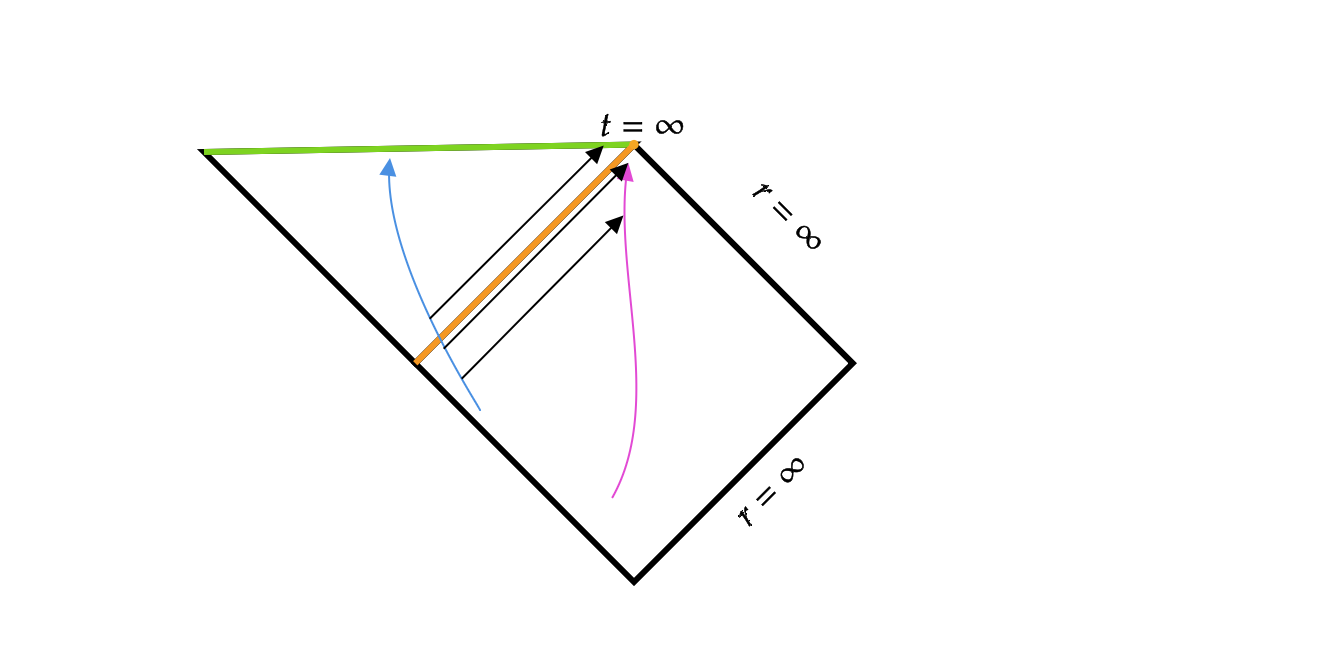
De blauwe pijl stelt een astronaut voor die zo dapper is geweest het zwarte gat in te springen. Terwijl de blauwe astronaut in het zwarte gat valt, stuurt die lichtsignalen naar een collega: de roze astronaut. Die blijft veilig (en misschien ook wel zo verstandig) buiten het zwarte gat, en vangt de lichtsignalen op. Het duurt alleen even voordat die lichtsignalen ver genoeg zijn gereisd om gezien te worden door de roze astronaut. Hoe dichter de blauwe astronaut bij de horizon komt, des te langer het duurt voor de uitgezonden lichtsignalen de roze astronaut bereiken. En eenmaal voorbij de horizon komen de lichtsignalen helemaal nooit meer aan bij de roze astronaut. Die ziet dus nooit de blauwe astronaut daadwerkelijk het zwarte gat in vallen! De blauwe astronaut merkt daar verder niets van: die passeert nietsvermoedend de horizon, tot onvermijdelijk de singulariteit dichter- en dichterbij komt…
Van zwarte naar witte gaten
De Schwarzschildmetriek beschrijft dus een zwart gat. Het is een zwart gat dat altijd heeft bestaan, en altijd zal bestaan. De metriek is zoals je in de formule kunt zien immers onafhankelijk van de tijd: voor elke waarde van \( t \) is de kromming overal hetzelfde. Dat geldt alleen niet voor de zwarte gaten die in de natuur voorkomen! Zwarte gaten, zoals we die vooral kennen, ontstaan als eindpunt van het leven van een heel zware ster. Zodra die ster niet meer genoeg brandstof heeft om zichzelf te beschermen tegen zijn eigen zwaartekracht, stort de ster ineen. Het resultaat, als de ster maar zwaar genoeg was, is een zwart gat. De Schwarzschildmetriek beschrijft dus bij goede benadering de ruimtetijd ná het vormen van zo’n zwart gat. Voor dat moment ziet de ruimtetijd er anders uit.
We moeten het Penrose-diagram dus niet al te serieus nemen als we het hebben over stellaire zwarte gaten, zwarte gaten die gevormd zijn als gevolg van de ineenstorting van een ster. Dit even terzijde; het eeuwige zwarte gat is gewoon een oplossing van de Einsteinvergelijkingen, die ons hebben gewezen op het bestaan van de mysterieuze objecten die zwarte gaten heten. We kunnen het eeuwige zwarte gat dus ook niet afdoen als een soort nutteloze, enkel theoretische, oplossing van de Einsteinvergelijkingen!
Einsteins vergelijkingen zijn overigens naast heel ingewikkeld, ook heel symmetrisch. Als alle coördinaten in een oplossing van teken wisselen, voldoet de nieuwe metriek nog steeds aan de wetten van de algemene relativiteit. Je kunt dat vergelijken met een bal die op de grond valt en weer omhoog stuit: als je een filmpje daarvan omdraait en spiegelt, zie je weer iets wat in de natuur zou kunnen gebeuren. Die symmetrie van Einsteins vergelijkingen is niet meteen terug te zien in de Penrose-diagrammen hierboven. Wat blijkt: de Schwarzschildmetriek is dan ook niet de volledige oplossing! We kunnen het domein van de coördinaten uitbreiden om uit te komen bij de maximaal uitgebreide Schwarzschildmetriek. Het bijbehorende Penrose-diagram ziet er als volgt uit:
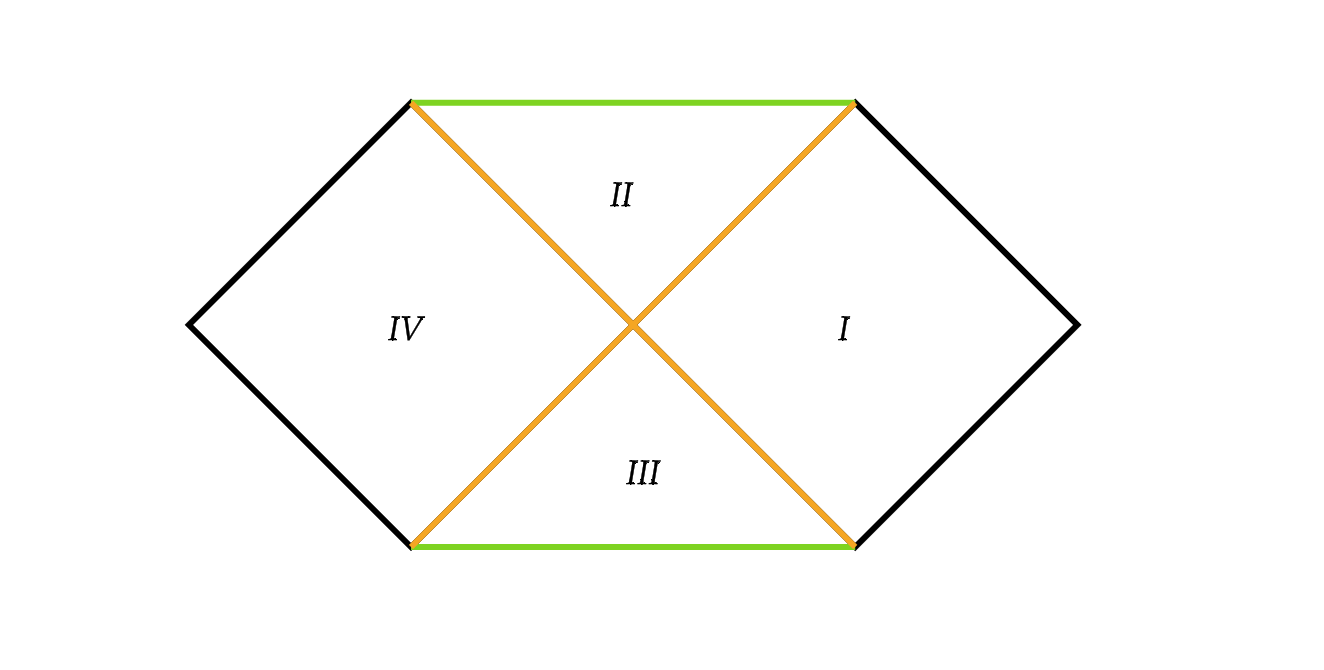
In dit Penrose-diagram wordt de symmetrie van de Einsteinvergelijkingen al duidelijker. Gebied I en II kenden we al vanuit de Schwarzschildmetriek: die beschrijven de gebieden respectievelijk binnen en buiten het zwarte gat. Maar in deze maximaal uitgebreide versie zijn er ook twee nieuwe gebieden bij gekomen: III en IV.
Eerst even over gebied IV. Het is een soort kopie van gebied I, maar dan ‘aan de andere kant’ van het zwarte gat. Vanuit gebied IV kan niets ooit gebied I bereiken en vice versa, dus vanaf buiten het zwarte gat gezien, vanuit gebied I, is dit gebied volledig onbereikbaar.
Laten we dus vooral gebied III eens wat beter bestuderen. Als we de regels van de Penrose-diagrammen er weer bij pakken, dan zien we dat alles wat begint in gebied III, uiteindelijk terecht moet komen in een van de andere drie gebieden. Anders gezegd: alles moet onherroepelijk weg uit gebied III. Dit is precies de definitie die we eerder aan een wit gat hadden gehangen! Natuurkundigen noemen gebied III dan ook inderdaad een wit gat. En vanuit het Penrose-diagram zien we meer: niet alleen moet alles verdwijnen uit het witte gat, er kan nooit iets van buiten het witte gat naar binnen vallen. Een wit gat is een zwart gat waarin de tijd is omgedraaid!
Dit is de zin waarin de meeste natuurkundigen het eens zijn over het bestaan van witte gaten: een theoretische mogelijkheid in de beschrijving van eeuwige zwarte gaten. Zoals ik eerder al schreef: de zwarte gaten die we kennen zijn géén eeuwige zwarte gaten, maar zijn ontstaan uit de ineenstorting uit een ster. Minder duidelijk is hoe (en of) een wit gat in zo’n geval ook zou kunnen ontstaan.
Witte gaten: echt of niet?
Een wit gat is dus een zwart gat waarin de tijd is omgedraaid. Een zwart gat vormt bijvoorbeeld doordat een ster ineenstort. Als we hierin de tijd omdraaien, explodeert een wit gat dan, waaruit een ster ontstaat? Dit lijkt de tweede wet van de thermodynamica tegen te spreken, die zegt dat entropie – grofweg ‘de hoeveelheid wanorde van een systeem’ – altijd moet toenemen. De entropie van een zwart (of wit) gat is namelijk véél groter dan die van een ster. Volgens veel natuurkundigen zijn witte gaten dus niets meer dan een theoretische oplossing van de Einsteinvergelijkingen – oplossingen die te veel vreemde eigenschappen hebben om echt te kunnen bestaan.
Er zijn echter ook natuurkundigen die deze theoretische beschrijving van witte gaten heel serieus nemen, en de mogelijkheid onderzoeken dat zulke witte gaten ook daadwerkelijk in ons universum bestaan. Onlangs nog kwam de Nederlandse vertaling van het boek Witte gaten van Carlo Rovelli uit, waarin hij schrijft over zijn onderzoek over witte gaten.
Carlo Rovelli doet onderzoek naar een versie van quantumzwaartekracht, lusquantumzwaartekracht genoemd – wie weet daarover meer in een later Quantum Universe-artikel. Binnen het raamwerk van die lusquantumzwaartekracht bestudeert hij de mogelijkheid dat een zwart gat, aan het einde van zijn leven, verandert in een wit gat.
Zoals ik eerder al noemde, draaien binnen in een zwart gat de rollen van ruimte en tijd om. De singulariteit op \( r=0 \) wordt binnenin het zwarte gat dus niet ervaren als het midden van het zwarte gat, maar als het einde der tijden, waarin de kromming oneindig sterk wordt. Volgens Rovelli is het op dit punt in de tijd, waar quantumeffecten dus onvermijdelijk een rol gaan spelen, mogelijk dat de ruimtetijd een bijzonder quantumeffect ondergaat: tunnelen.
Binnen de quantumfysica is tunnelen een welbekend fenomeen, waarbij quantumdeeltjes kunnen ‘springen’ in de ruimte, waar dat volgens de klassieke mechanica niet mogelijk is. Volgens Rovelli is het in de lusquantumzwaartekracht ook mogelijk dat niet alleen wordt getunneld in de ruimte, maar ook in de ruimtetijd. Het zwarte gat kan volgens hem tunnelen naar een wit gat. Een beetje zoals een bal die op de grond stuitert en weer omhoogkomt, stuitert volgens Rovelli een zwart gat naar een wit gat. Het bestaan van zware witte gaten is hierin nog steeds heel onwaarschijnlijk: de materie die eruit komt, zal snel botsen met de materie die eromheen draait en dus zal het systeem ineenstorten tot een zwart gat. Maar een klein en licht wit gat zou volgens de aanhangers wel stabiel kunnen zijn. Dit witte gat straalt vervolgens al zijn massa en informatie weg, tot het helemaal is verdwenen.

In de natuurkundige wereld is er nog geen consensus over de vraag of witte gaten wel of niet bestaan. Volgens de algemene relativiteitstheorie kunnen ze bestaan, maar de bijzondere implicaties die ze met zich meebrengen zijn voor veel natuurkundigen reden om te geloven dat ze niet meer zijn dan dat: een theoretische mogelijkheid. Maar goed, die status hadden zwarte gaten ooit ook…
[1] Het is natuurlijk ook mogelijk om zó te bewegen dat je nooit in het zwarte gat valt, maar ook nooit oneindig ver weg komt. Al deze paden – de ‘minst interessante’ voor waar we hier in geïnteresseerd zijn – zullen in het Penrose-diagram eindigen in het punt waar de groene en de oranje lijn samenkomen; dat ene punt geeft dus de situatie ‘na oneindig veel tijd, maar niet oneindig ver weg’ weer.