
Afbeelding 1. Dobbelstenen.Hoe laat je een computer zó ‘met dobbelstenen gooien’ dat de uitkomst een echt willekeurige reeks getallen is? Foto: PickPik.
Om nader te verklaren waarom het gebrek aan correlatie zo’n big deal is, gaan we eerst even terug in de tijd. Binnen de natuurkunde is, sinds de opmars van computers in de vorige eeuw, een nieuwe tak van sport ontstaan: computationele natuurkunde. De naam zegt het al: men doet natuurkunde door keihard te rekenen met computers. Meestal komen we, bij een bepaald probleem, lastige formules tegen, die simpelweg niet met alleen pen en papier op te lossen zijn. Als voorbeeld kun je denken aan integralen waarvoor geen analytische oplossing is, en waarvoor alleen maar numerieke antwoorden bestaan. Een belangrijk gereedschap dat nodig is voor computationele natuurkunde, is het beschikken over ‘random numbers’, willekeurige getallen. Voor het numeriek evalueren van integralen bestaat er bijvoorbeeld zoiets als de ‘Monte Carlomethode’. Deze methode berekent de integraal simpelweg door random getallen te kiezen, en dan te kijken of deze getalen aan een bepaalde eis voldoen. De verhouding van ‘goede getallen’ (die aan de eis voldoen) tot ‘afgekeurde getallen’ vertelt je dan iets over het numerieke antwoord op de integraal. Zo kun je bijvoorbeeld een oppervlak berekenen (iets wat typisch met een integraal wordt gedaan) door als ‘eis’ te kiezen dat willekeurige punten binnen dat oppervlak vallen – zie afbeelding 2. Dé belangrijke eigenschap die bepaalt dat deze methode een goed antwoord geeft, is dat de getallen die je gebruikt volledig random zijn. En dit voorbeeld is slechts één van vele. Daarnaast spelen random getallen in andere takken van de wetenschap ook een zeer belangrijke rol. Cryptografie heeft bijvoorbeeld ook vaak als grondslag een reeks van random getallen nodig.
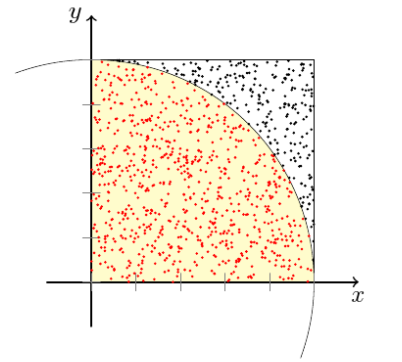
Afbeelding 2. Een Monte Carlosimulatie.Een schematische weergave van een Monte Carlosimulatie. De punten in het vierkant zijn allemaal random gekozen. De rode punten zijn ‘geaccepteerde getallen’, en de zwarte zijn ‘geweigerde getallen’. De verhouding tussen het totaal aantal random getallen en goede getallen is gelijk aan de verhouding van het vierkant tot het gele oppervlak. Met deze methode zou je bijvoorbeeld de numerieke waarde van het getal π kunnen bepalen. Afbeelding: Springob.
Goede random getallen zijn echter niet makkelijk te genereren. Zelf een miljard keer een dobbelsteen opgooien is geen optie. Dit zou veel te lang duren. Uiteraard denkt iedereen (terecht) met zulke grote aantallen: “dat laten we computers oplossen”. Helaas zijn computers bij uitstek ongeschikt voor deze taak. Bedenk immers: hoe vertel je een computer om je één miljard random getallen te geven? Een computer is een deterministische machine, wat wil zeggen dat hij alleen maar dat kan doen wat expliciet van hem gevraagd wordt. Het antwoord is dus per definitie niet ‘random’. Gelukkig was er na de opkomst van de computers al vrij snel een manier ontwikkeld om toch de droom van random getallen waar te maken, namelijk de methode van pseudo-random numbers. Een computerprogramma dat deze getallen genereert, heeft als output een serie getallen die heel erg lijken op random getallen. Ze zijn het echter niet! De wiskundige John von Neumann, die als een van de eerste een algoritme introduceerde voor het genereren van zulke pseudo-random numbers zei zelf al dat het halen van échte random getallen uit een computer waanzin was. Het probleem van pseudo-random getallen is: als je maar genoeg van zulke getallen produceert zal er, uiteindelijk, toch een patroon onstaan. Dezelfde getalpatronen herhalen zich, of er ontstaan correlaties (onderlinge verbanden) tussen bepaalde getallen. Dit zijn allemaal artefacten van het feit dat een computer deterministisch is.
Om dit te illustreren nemen we een concreet voorbeeld. Een bekend algoritme voor het bepalen van een pseudo-random getallenreeks is die van de ‘linear congruential generator’. De getallenreeks wordt geproduceerd aan de hand van de volgende formule:
\(x_n = (a \, x_{n-1} + c) \mbox{ mod } m\)
In woorden: Het volgende getal wordt bepaald door het vorige getal, vermenigvuldigd met een constante a, en vermeerderd met een constante c. Als laatste kijk je of het uiteindelijke getal kleiner is dan een bepaalde bovengrens m; als dat niet het geval is haal je net zo lang m van het getal af tot het onder de bovengrens komt. Deze formule creëert daarmee pseudo-random getallen tussen 0 en m-1. De kwaliteit van deze pseudo random getallen hangt heel erg af van de constantes a, c en m. Een goede keus is bijvoorbeeld a = 16807, c = 0, m = 231 -1. (m is dus heel groot!) Het probleem van deze reeks is niet heel moeilijk in te zien. Men kan een getallenreeks maken die op zijn hoogste m getallen groot is; daarna kom je onvermijdelijk een getal tegen dat al een keer aan de beurt is geweest, en zal dezelfde reeks zich herhalen. 231 is weliswaar een groot getal (ongeveer 2 miljard), maar met de gigahertz-computers van tegenwoordig kost het slechts enkele tientallen seconden om deze reeks helemaal te doorlopen.
Er bestaan betere algoritmes, die langere en betere random getallen genereren. Desondanks is deze queeste gedoemd te mislukken. PCs zijn deterministisch, en zullen dat altijd blijven.
Is er dan geen manier om dit probleem fundamenteel op te lossen? Toch wel! Zoals je als lezer van deze website wellicht al weet, bestaan er in de natuur objecten die juist wél echt random zijn. Uiteraard heb ik het hier over quantummechanische objecten. Deze randomness van quantummechanische verschijnselen zou een oplossing kunnen zijn voor ons probleem. Die oplossing is inmiddels ook toegepast: er bestaan tegenwoordig échte random number generators. Deze apparaten kunnen op basis van bijvoorbeeld LEDs (zie afbeelding 3) echte random getallen generen.
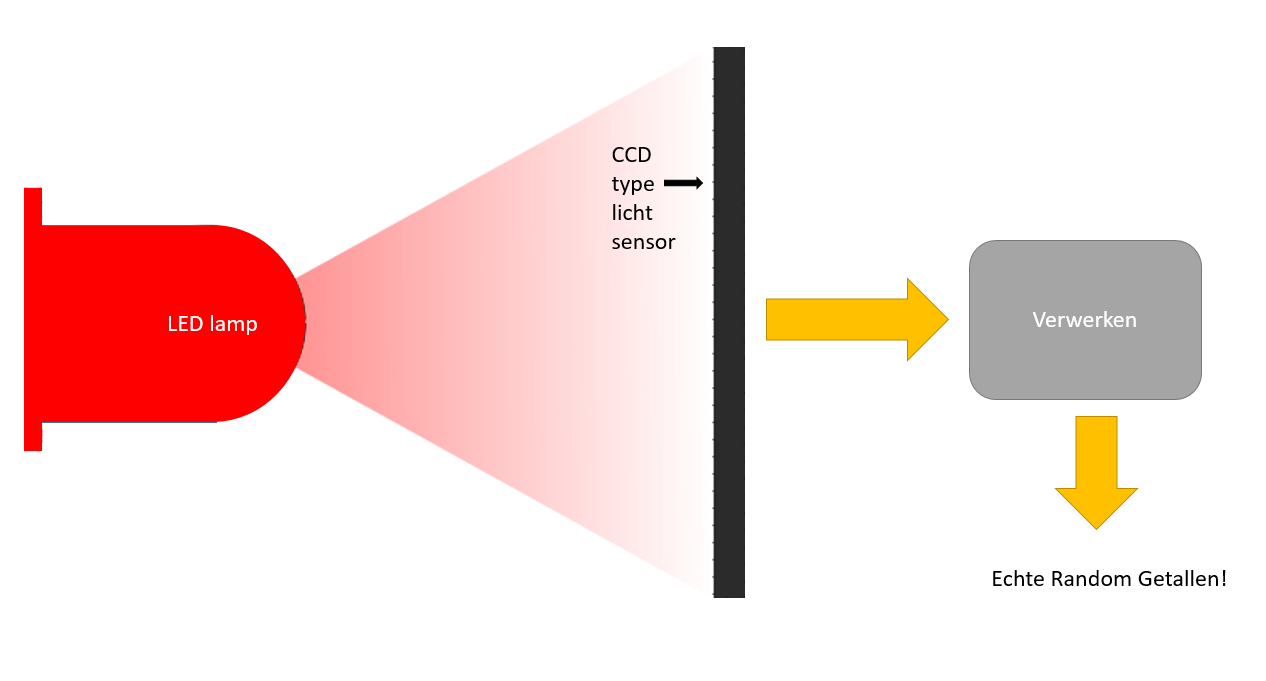
Afbeelding 3. Een quantum random number generator.Schematische weergave van een echte quantum random number generator. Het licht schijnt op een camera met een CCD-sensor die telt hoeveel lichtdeeltjes er op elk punt vallen. Het aantal fotonen dat een pixel van de CCD sensor zo meet is van nature random. Deze toevalligheid wordt door een andere chip verwerkt en omgezet in een serie random getallen.
Quantum random number generators zijn momenteel te koop in het formaat van een chip die je zo in je computer kan steken. Toch zijn er nog de nodige problemen met deze chips. De snelheid waarmee ze getallen produceren is vaak lang niet goed genoeg om binnen praktische tijd grote reeksen getallen te produceren. Onderzoekers zijn nog elke dag bezig om random number generators beter en sneller te maken. Desondanks is het onwaarschijnlijk dat gewone consumenten binnenkort al een random nummer chip in hun pc bouwen. Deze hardware zal waarschijnlijk wel snel zijn weg vinden naar commerciële bedrijven.
Op internet bestaan enkele sites die je kan vragen om je te voorzien van echte quantum random numbers, zoals bijvoorbeeld https://qrng.anu.edu.au/API/api-demo.php. Daar zijn ook de getallen in de titel van dit stuk vandaan gehaald.