
Afbeelding 1. De Einsteinvergelijking.Robbert Dijkgraaf bij het onthullen van de Einsteinvergelijking. Met dank aan Ivo van Vulpen voor het ter beschikking stellen van de foto (tevens foto in het blokkenschema op de voorpagina).
Algemene relativiteitstheorie
In 1905, tien jaar voor het verschijnen van zijn artikel over de algemene relativiteitstheorie, had Einstein zijn andere beroemde theorie gepubliceerd: de speciale relativiteitstheorie. In die theorie beschreef hij hoe ruimte en tijd gezien moeten worden als onderdeel van één geheel, de ruimtetijd. Het samenvoegen van die twee concepten was niet alleen een wiskundige truc. Het bleek ook mogelijk om ermee uit te rekenen hoe verschillende, onderling bewegende waarnemers afstanden en tijdsintervallen tussen gebeurtenissen meten.
Het resultaat was zeer verrassend. Waar in het verleden altijd gedacht was dat afstanden en tijdsintervallen absolute, waarnemeronafhankelijke begrippen waren, liet Einstein zien dat twee onderling bewegende waarnemers verschillende waarden kunnen meten voor de afstand of de tijd tussen twee bepaalde gebeurtenissen. Die verschillen worden pas significant als de onderlinge snelheid tussen de waarnemers van de orde van de lichtsnelheid wordt – die is zo’n 300.000 kilometer per seconde – maar desondanks is het inmiddels uitgebreid gelukt om de voorspellingen van de speciale relativiteitstheorie te testen. Ruimtetijd is een absoluut concept, maar ruimte en tijd afzonderlijk blijken dat niet te zijn!
De speciale relativiteitstheorie is een prachtig en accuraat model van de natuur, maar de theorie had één groot gemis: ze beschreef alleen hoe waarnemers die met constante onderlinge snelheid bewegen, de natuur ervaren. Hoe zit het als een van de waarnemers ten opzichte van de ander versnelt? Die ogenschijnlijk eenvoudige vraag bleek grote gevolgen te hebben. Het kostte Einstein tien jaar om de vraag volledig in detail te beantwoorden; het uiteindelijke antwoord was de algemene relativiteitstheorie.
De zwaartekracht doet zijn intrede
Het belangrijkste inzicht dat Einstein naar de algemene relativiteitstheorie leidde, was dat het begrip versnelling sterk verbonden is met het begrip zwaartekracht. Eén kant op is dat verband overduidelijk: wie zich in een zwaartekrachtsveld bevindt – bijvoorbeeld dat van de aarde – zal ook versneld worden: in dit voorbeeld naar de aarde toe. Einsteins inzicht was dat het verband omgedraaid kan worden: wie versnelt, ervaart dat alsof hij of zij zich in een zwaartekrachtsveld bevindt! Het beroemde voorbeeld is de waarnemer die in een geblindeerde lift staat. Als de lift omhoog versnelt, voelt de waarnemer zich zwaarder worden. Het lijkt experimenteel dus niet mogelijk te zijn om het verschil te meten tussen versnelling zonder zwaartekracht, en zwaartekracht zonder versnelling!

Afbeelding 2. Zwaartekracht en versnelling.Een waarnemer in een versnellende lift in de ruimte ervaart exact hetzelfde als een waarnemer in een stilstaande lift op aarde.
De laatste stap die Einstein nodig had om zijn theorie compleet te maken was de volgende. Als de waarnemer in de lift extreem nauwkeurig zou meten, zou hij wellicht tóch het verschil kunnen meten tussen de stilstaande lift in het zwaartekrachtsveld van de aarde en de versnellende lift daarbuiten. In de versnellende lift zullen twee voorwerpen die hij loslaat namelijk recht naar beneden ‘vallen’; in de lift die stilstaat op aarde vallen de twee voorwerpen naar het middelpunt van de aarde toe – en wijken ze dus een minieme hoeveelheid af van een verticale, rechte baan.
Die observatie leidde Einstein tot de conclusie dat het juist de afwijking van rechte banen is die bepaalt wat zwaartekracht is. Die afwijking manifesteert zich in zijn ruimtetijdbeeld als volgt: om zwaartekracht in de ruimtetijd te kunnen beschrijven, kunnen we niet langer aannemen dat die ruimtetijd plat is. We moeten de ruimtetijd daarvoor krom maken. Materie (zoals het vallende voorwerp in de stilstaande lift) beweegt door die kromme ruimtetijd in ‘zo recht mogelijke’ banen; de afwijking van daadwerkelijk rechte banen is wat wij ervaren als zwaartekracht.
De linkerkant van de vergelijking
Algemene relativiteitstheorie is in zekere zin dus meetkunde: om een zwaartekrachtsveld te beschrijven, moeten we de kromming van de ruimte en de tijd beschrijven. De wiskundige beschrijving van dergelijke kromming was in 1915 al bekend: die was ontwikkeld door de negentiende-eeuwse Duitse wiskundige Bernhard Riemann. De nogal gecompliceerd ogende linkerhelft van de formule van Einstein,
Rμν – ½ R gμν + Λ gμν
beschrijft, in termen van de door Riemann gebruikte ’tensorrekening’, de kromming van de ruimte en tijd op elk punt en op elk moment.

Afbeelding 3. Bernhard Riemann (1826-1866).Riemann beschreef de meetkunde van kromming met behulp van tensorrekening. Deze tensorrekening gebruikte Einstein vervolgens in zijn algemene relativiteitstheorie.
Opvallend is overigens dat in de formule die nu op de gevel van het Boerhaave-museum prijkt drie termen aan de linkerkant staan. Om met de tensorrekening van Riemann de kromming in het heelal te beschrijven, zouden in de meeste gevallen de eerste twee termen voldoende zijn. Het viel Einstein echter bij het afleiden van zijn theorie op dat er geen enkel wiskundig argument was te vinden om niet nog een derde term op te schrijven; een term die een soort ‘constante achtergrondkromming’ van het heelal beschrijft. Vergelijk dit met de kromming in het oppervlak van een ballon: we kunnen de ballon plaatselijk indeuken, wat tot kromming leidt, maar ook als we de ballon met rust laten, heeft elk stuk van zijn oppervlak een bepaalde kromming. Het is deze gemiddelde kromming die overal aanwezig is – ook wel de cosmologische constante genoemd – die beschreven wordt door de derde term aan de linkerkant van Einsteins vergelijking.
Einstein zag zoals gezegd geen wiskundige reden waarom zo’n achtergrondkromming niet in het heelal aanwezig kon zijn, maar hij zag ook geen natuurkundige reden waarom zo’n achtergrondkromming er wel zou zijn. Hij schreef de term in zijn oorspronkelijke artikel dus op, maar zou later de beroemde uitspraak hebben gedaan dat dit de “grootste blunder uit zijn carrière” was. Sinds de jaren ’90 weten we echter dat het hier beslist niet gaat om een blunder: het heelal heeft wel degelijk een kleine achtergrondkromming, en de term met de cosmologische constante in de Einsteinvergelijking is dus essentieel voor het beschrijven van ons heelal!
De rechterkant van de vergelijking
De linkerkant van Einsteins vergelijking beschrijft dus de kromming van de ruimtetijd. De volgende vraag is natuurlijk: wat veroorzaakt deze kromming? We weten inmiddels dat kromming gelijk staat aan zwaartekracht, en zwaartekracht wordt veroorzaakt door massa. Hoe zwaarder een object zoals een ster of een planeet, hoe sterker zijn zwaartekracht – en hoe meer de ruimte eromheen dus gekromd zou moeten worden.
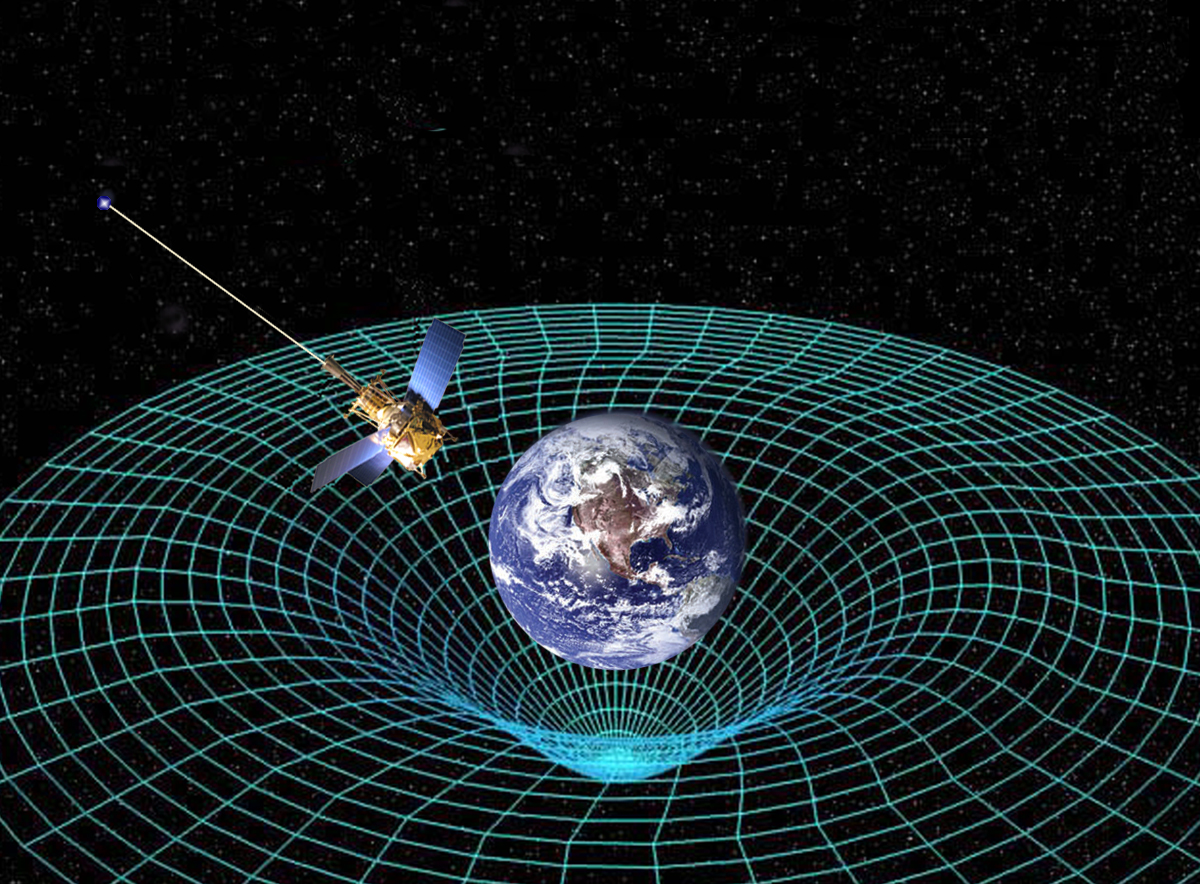
Afbeelding 4. Materie en kromming.Materie – hier: de aarde – veroorzaakt zwaartekracht, en kromt dus de ruimtetijd om zich heen. Afbeelding: NASA.
Nu was uit de speciale relativiteitstheorie al bekend dat massa een vorm van energie is. De beroemde formule E=mc2 drukt dit uit: een bepaalde hoeveelheid massa (m) kan omgerekend worden in een equivalente hoeveelheid energie (E) door de massa te vermenigvuldigen met het kwadraat van de lichtsnelheid. Massa kan omgezet worden in andere vormen van energie – de kerncentrale en de atoombom zijn daarvan de bekende voorbeelden. Omgekeerd kan ook: energie kan worden omgezet in massa. Dit is precies wat er gebeurt in deeltjesversnellers zoals die op het CERN in Genève: bij botsingen met enorme hoge energieën ontstaan daar allerlei nieuwe deeltjes.
Als massa en energie equivalent aan elkaar zijn, is het dan ook zo dat energie de ruimte kan krommen? Einstein toonde aan dat het antwoord ‘ja’ moet zijn. Elke vorm van energie is in staat om de ruimte en de tijd te krommen. Dit idee wordt weergegeven in de rechterkant van de Einsteinvergelijking: de uitdrukking
Tμν
staat voor de energiedichtheid (nog iets preciezer: de dichtheid van energie en impuls) op elk punt in de ruimte en in de tijd. Om tot precies de juiste waarde voor de kromming te leiden moet deze energiedichtheid nog vermenigvuldigd worden met enkele natuurconstanten: de zwaartekrachtsconstante van Newton, G, de getallen 8 en π, en één gedeeld door de vierde macht van de lichtsnelheid, c.
In woorden zegt Einsteins vergelijking dus het volgende: op elk punt in de ruimte en op elk moment in de tijd wordt de plaatselijke kromming van die ruimtetijd bepaald door de hoeveelheid aanwezige energie. Wanneer we beseffen dat de energie die voor de kromming zorgt met name het gevolg is van de massa van materie, en dat die materie zélf natuurlijk ook door de ruimte en de tijd beweegt, kunnen we de Einsteinvergelijking ook formuleren in de beroemde woorden van de fysicus John Archibald Wheeler: ‘spacetime tells matter how to move; matter tells spacetime how to curve‘. Het is dit spel van ruimte, tijd en materie waarvan Einstein honderd jaar geleden als eerste de regels begreep.
Meer weten over de relativiteitstheorie? Lees dan ook ons dossier over dit onderwerp.