Zwarte gaten (14): Overzicht

In dit artikel:

• Zwarte gaten
• Relativiteit en quantummechanica
• De vragen
• Het begin van antwoorden
• En nu?

Afbeelding 1. Een zwart gat.Een ‘artist impression’ van een zwart gat dat een nabijgelegen ster langzaam opslokt. Afbeelding: NASA.

Zwarte gaten

Aan het begin van dit dossier definieerden we wat een zwart gat is: een plek in het heelal waar de zwaartekracht zo sterk is dat zelfs licht niet snel genoeg beweegt om aan die plek kan ontsnappen. In die korte definitie zitten al verschillende belangrijke natuurkundige ideeën besloten. Allereerst het feit dat licht een snelheid heeft. Als we het licht aandoen in een kamer, is die niet instantaan verlicht, maar duurt het een fractie van een seconde voordat het licht uit de lamp alle voorwerpen in de kamer en vervolgens onze ogen heeft bereikt. Dat we dat niet merken, komt door de enorme snelheid van het licht: dat beweegt met maar liefst 300.000 kilometer per seconde.

Ten tweede zien we aan bovenstaande definitie van zwarte gaten dat de centrale eigenschap, die zegt of iets aan een zwart gat kan ontsnappen, de snelheid van dat voorwerp is. Het maakt niet uit hoe zwaar een object is; om zonder hulp aan een bepaald zwaartekrachtsveld te ontsnappen moet het een bepaalde vaste snelheid hebben – de zogenaamde ontsnappingssnelheid. Is die ontsnappingssnelheid hoger dan die van het licht, dan kan dus ook het licht niet ontsnappen, en is er een zwart gat ontstaan.

Tenslotte bevat de definitie het wat onopvallende maar cruciale woordje ‘zelfs’: een zwart gat is een plek waar zelfs het licht niet aan kan ontsnappen. In dat woordje ligt besloten dat, zoals Albert Einstein liet zien met zijn relativiteitstheorie, niets sneller kan bewegen dan het licht. Zodra er aan een plek in het heelal geen licht kan ontsnappen, kan er dus volgens de relativiteitstheorie helemaal niets ontsnappen! Dat maakt zwarte gaten zo interessant: ze lijken – in elk geval op het eerste gezicht – alles om zich heen voor altijd en eeuwig op te slokken.

Afbeelding 2. M61.We kunnen zwarte gaten niet direct zien, maar de gevolgen van hun aanwezigheid worden tegenwoordig op veel plaatsen in het heelal waargenomen. Hier het sterrenstelsel M61, waarvan gedacht wordt dat de kern een enorm zwart gat bevat. Foto: NASA.

Een zwart gat ontstaat zodra heel veel materie zich in een heel kleine hoeveelheid ruimte bevindt. Dan wordt de zwaartekracht sterk genoeg om ook het licht te ‘vangen’. In een laboratorium is het vrijwel onmogelijk om dergelijke omstandigheden te creëren. In het algemeen zal zoiets dus diep in het heelal gebeuren – bijvoorbeeld als de kern van een opgebrande ster ineenstort, of als in het centrum van een sterrenstelsel zo veel sterren bij elkaar komen dat een enorm zwaartekrachtsveld ontstaat. Hoewel een zwart gat geen licht uitzendt, en we een zwart gat dus nooit direct kunnen ‘zien’, kunnen we aan de hand van allerlei randeffecten en metingen van de zwaartekracht aantonen dat er zich in het heelal talloze zwarte gaten bevinden. Het doen van directe metingen aan die zwarte gaten is natuurlijk een stuk lastiger – vandaar dat de studie van zwarte gaten zich vooralsnog met name op het theoretische vlak afspeelt.

Naar boven

Relativiteit en quantummechanica

Zodra een zwart gat ontstaat, ontstaat daarmee ook een horizon: een denkbeeldige schil rond het zwarte gat waar de zwaartekracht precies zo sterk is dat de ontsnappingssnelheid gelijk is aan de lichtsnelheid. Dichter bij het zwarte gat is de ontsnappingssnelheid hoger, en kan niets dus meer ontsnappen; verder weg is de ontsnappingssnelheid lager en is ontsnappen in principe nog mogelijk. De horizon is dus ’the point of no return’ – of nauwkeuriger: ’the surface of no return’.

De omschrijving hierboven aan de hand van een ontsnappingssnelheid is overigens wat kort door de bocht. Een creatieve geest zou zich kunnen bijvoorbeeld kunnen afvragen of het niet mogelijk is om met een sterke motor langzaam van binnen naar buiten de horizon te bewegen en vervolgens alsnog te ontsnappen. Om te kunnen inzien dat dat niet mogelijk is, riepen we in het derde artikel in deze serie de hulp in van de algemene relativiteitstheorie. Aan de hand daarvan zagen we wat er écht op de horizon gebeurt: daar wordt in zekere zin de ruimte zelf met de lichtsnelheid naar binnen gezogen. Zelfs met de sterkste motor valt daar dus niet tegenop te bewegen!

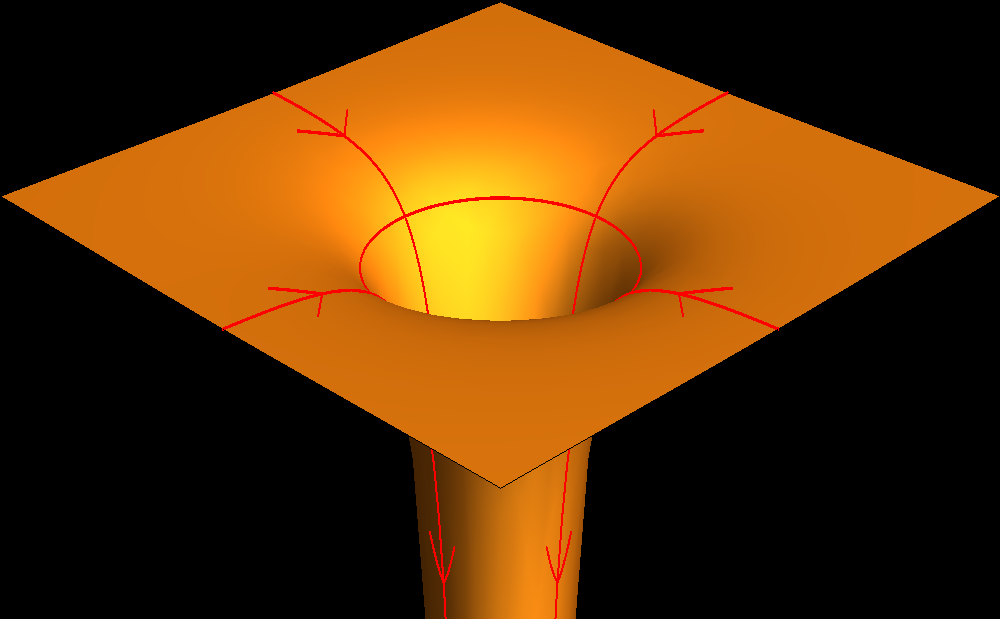
Afbeelding 3. Een relativistische weergave van een zwart gat.Het gele oppervlak is een tweedimensionaal model van de ruimte rond een driedimensionaal zwart gat. De ruimte wordt met steeds grotere snelheid een diepe “put” in gezogen. Op de plek van de rode cirkel is die snelheid precies de lichtsnelheid: dit is de horizon van het zwarte gat.

De relativiteitstheorie maakt zwarte gaten al erg interessant, maar nóg interessanter wordt het als we ook de quantummechanica in het verhaal betrekken. Dan blijkt namelijk dat zwarte gaten toch niet zo zwart zijn als ze in eerste instantie lijken. In de quantummechanica is zelfs een lege ruimte namelijk nooit helemaal leeg: daarin ontstaan en verdwijnen continu paren van deeltjes en antideeltjes. In het vierde artikel in dit dossier zagen we dat dat in combinatie met de relativiteitstheorie uiteindelijk betekent dat er deeltjes aan het zwarte gat kunnen ontsnappen: de zogeheten Hawkingstraling, vernoemd naar de ontdekker van dit verschijnsel, Stephen Hawking. Die Hawkingstraling – en de combinatie van relativiteit en quantummechanica waaruit het bestaan van die straling volgt – geeft aanleiding tot de twee fundamentele vragen die het huidige theoretische onderzoek naar zwarte gaten zo interessant maken.

Naar boven

De vragen

Een eerste vraag over zwarte gaten volgt direct uit het bestaan van Hawkingstraling. Zoals we hierboven hebben beschreven, lijkt die namelijk in de buurt van de horizon van het zwarte gat te ontstaan, en lijkt de straling daarmee geen informatie te bevatten over wat er zich in het zwarte gat afspeelt – of over hoe en waaruit het zwarte gat oorspronkelijk is gevormd. Datzelfde volgt ook uit de oorspronkelijke berekeningen van Stephen Hawking: die liet zien dat de straling van een zwart gat  ’thermisch’ is, wat wil zeggen dat de eigenschappen van die straling alleen afhangen van de temperatuur van het zwarte gat, en dus niet van welke andere eigenschap dan ook.

Dat leidt tot een vreemde paradox. In de natuurkunde zijn we gewend dat informatie behouden blijft. Dat wil zeggen: als we de eindsituatie van een proces of experiment maar nauwkeurig genoeg kennen, kunnen we ook terugrekenen en achterhalen wat de beginsituatie was. Dat is niet alleen een ervaringsfeit: we kunnen dat ook bewijzen aan de hand van de wiskundige formulering van de natuurwetten. Het vreemde is nu dat dit behoud van informatie geldt voor zowel de relativiteitstheorie als de quantummechanica, maar dat zwarte gaten toch informatie lijken te vernietigen. De informatie verdwijnt immers achter de horizon – en alsof dat nog niet vreemd genoeg is, lijkt het erop dat het zwarte gat vervolgens ook nog eens helemaal kan verdampen, terwijl het alleen maar thermische straling uitzendt. Na afloop van dat proces is het zwarte gat verdwenen; de informatie over hoe het gevormd is lijkt dus ook niet meer te achterhalen. Een heel vreemd resultaat, aangezien we voor de redeneringen die ertoe leidden juist gebruik hebben gemaakt van twee theorieën waarin informatie niet verloren kan gaan! Deze vreemde situatie wordt de informatieparadox genoemd.

Afbeelding 4. De informatieparadox.Wat gebeurt er met de informatie die in een zwart gat valt?

De bovenstaande beschrijving van de informatieparadox kan nog veel preciezer worden gemaakt als we de paradox in quantummechanische termen beschrijven. We deden dit in het zevende artikel van dit dossier, waarin we zagen dat de informatieparadox inhoudt dat een quantummechanische superpositie van toestanden, waarin alle quantuminformatie bekend is en kansprocessen alleen op fundamentele quantumschaal een rol spelen, door een zwart gat omgezet lijkt te worden in een ‘statistische’ combinatie van toestanden, waarin het juist onze onwetendheid is die het kanskarakter van de toestand bepaalt. Deze omzetting van ‘fundamentele kansen’ naar ‘kansen door onwetendheid’ blijkt het punt te zijn waarop de informatie over het systeem verloren gaat.

Een tweede raadsel rond zwarte gaten volgt uit de thermodynamica van deze objecten. Zoals we al zagen, hebben zwarte gaten door hun Hawkingstraling een temperatuur, en daarmee kunnen we proberen om ze te beschrijven aan de hand van dezelfde wetten van de thermodynamica waarmee we ook het afkoelen van een kop koffie of het mengen van gassen beschrijven. Dat blijkt verrassend goed te gaan: zwarte gaten voldoen aan alle wetten van de thermodynamica. In het bijzonder hebben zwarte gaten ook een entropie: een eigenschap die grofweg zegt hoeveel arbeid het zwarte gat bij een bepaalde temperatuur kan verrichten. De entropie van een zwart gat blijkt ook eenvoudig te berekenen. Zoals Stephen Hawking en Jacob Bekenstein lieten zien, is die entropie (gemeten in de juiste eenheden) gelijk aan een kwart van de grootte van het oppervlak van de horizon.

In ‘normale’ thermodynamische systemen, zoals een kop koffie of een ballon met heliumgas, is het echter altijd zo dat de entropie ook op een heel andere, microscopische manier bepaald kan worden. Die systemen bestaan namelijk uit een gigantisch aantal microscopische bouwstenen: de vloeistofmoleculen in de koffie, de heliumatomen in de ballon. Zoals Ludwig Boltzmann in de 19e eeuw liet zien, kan de entropie van zo’n systeem exact berekend worden door te bepalen op hoeveel verschillende manieren die bouwstenen gerangschikt kunnen worden om een systeem met de juiste eigenschappen (druk, temperatuur, volume, enzovoort) te vormen.

Afbeelding 5. Een kop koffie.De thermodynamica van een kop koffie kunnen we begrijpen aan de hand van de moleculen waaruit de koffie bestaat. Kunnen we op soortgelijke manier de thermodynamica van zwarte gaten begrijpen? Foto: Padurariu Alexandru.

De grote vraag is dus: kan dit voor een zwart gat ook? Kunnen we achterhalen wat de bouwstenen van een zwart gat zijn, en vervolgens de mogelijke microscopische toestanden van een zwart gat tellen? Wat deze vraag extra interessant maakt is dat die gaat over de microscopische eigenschappen van extreem relativistische systemen . Om de vraag te beantwoorden moeten we dus goed begrijpen hoe de quantummechanica en de relativiteitstheorie samenwerken. En juist die vraag is één van de grote open vragen in de huidige theoretische natuurkunde.

Naar boven

Het begin van antwoorden

Op beide hierboven genoemde vragen is het exacte antwoord op dit moment niet bekend. Toch is er de laatste (tientallen) jaren veel onderzoek gedaan naar zowel de informatieparadox als het tellen van toestanden van zwarte gaten, en is er op beide terreinen veel vooruitgang geboekt.

Wat de informatieparadox betreft: een groot deel van de fysici is het er inmiddels over eens dat bij het verdampen van een zwart gat de informatie tóch op de een of andere manier behouden blijft. Onder die fysici is ook Stephen Hawking zelf. Dat Hawking en anderen ervan uitgaan dat informatie niet verloren gaat, komt door het holografisch principe – een idee dat zegt dat het vaak mogelijk is om de wiskundige beschrijving van één natuurkundige theorie te vertalen in de wiskundige beschrijving van een andere theorie. Ook voor veel zwaartekrachtstheorieën waarin zwarte gaten voorkomen blijkt zo’n ‘duale’ beschrijving te bestaan, en in die duale theorieën is het vaak mogelijk om te bewijzen dat informatie niet verloren gaat. Daarmee moet de informatie dus ook in de oorspronkelijke theorie behouden blijven, en hebben we dus een ‘achterdeurbewijs’ voor het behoud van informatie. Overigens: over het holografisch principe dat aan deze bewijzen ten grondslag ligt, begint vanaf volgende week een nieuw dossier op deze website. Wie geïnteresseerd is in de details kan vanaf dan dus zijn hart ophalen.

Afbeelding 6. Een hologram.In een ‘gewoon’ hologram bevat een tweedimensionale afbeelding volledige informatie over een driedimensionaa object. Op dezelfde manier kan volgens het holografisch principe de ene natuurkundige theorie volledige informatie bevatten over de andere. Hologram: Georg-Johann Lay.

Het nadeel van deze holografische redenering is dat die ons niets leert over hoe de informatie behouden blijft, en wat er precies mis was met de oorspronkelijke redenering van Hawking. Bovendien kunnen dualiteiten vaak wel stevig onderbouwd worden, maar zelden in volledig wiskundig detail bewezen. De informatieparadox is daarmee dus zeker nog niet opgelost!

In de afgelopen decennia hebben natuurkundigen diverse ideeën ontwikkeld over wat de fysica achter het al dan niet behouden van informatie is. Een belangrijke rol daarin speelt het concept van complementariteit dat we in het achtste artikel uit dit dossier tegenkwamen. Dit concept is erop gebaseerd dat in veel moderne theorieën de waarnemer een centrale rol speelt: natuurverschijnselen kunnen door verschillende waarnemers op verschillende manieren worden geïnterpreteerd. Denk aan de relativiteitstheorie, waarin twee gebeurtenissen die voor één persoon gelijktijdig zijn, voor een andere persoon op heel verschillende tijdstippen kunnen gebeuren. Complementariteit trekt dit idee door naar het begrip informatie: informatie die zich voor een ‘invallende’ waarnemer binnen het zwarte gat lijkt te bevinden, kan zich voor een waarnemer op afstand prima buiten het zwarte gat bevinden.

Nu heeft dit begrip van complementariteit zo zijn haken en ogen. Zo lieten de natuurkundigen Almheiri, Marolf, Polchinski en Sully zien dat het idee, in combinatie met een aantal andere voor de hand liggende aannames, leidt tot de conclusie dat een astronaut die een zwart gat in valt op de horizon een firewall tegenkomt: een ‘muur’ van hete materie waarin die astronaut onherroepelijk verbrandt. Deze conclusie is in sterke tegenspraak met wat we aan de hand van alleen de relativiteitstheorie zouden verwachten: die theorie zegt juist dat er op de horizon van een zwart gat helemaal niets bijzonders gebeurt, en dat de astronaut die horizon zonder iets te merken zal passeren.

Een wellicht minder extreme oplossing voor de informatieparadox ligt in het idee van fuzzballs dat afkomstig is van de Indiase natuurkundige Samir Mathur. Zijn idee is gebaseerd op de snaartheorie, een van de weinige theorieën die erin slaagt om de relativiteitstheorie en de quantummechanica in zich te verenigen. In de snaartheorie zijn de elementaire bouwstenen van het heelal geen puntvormige deeltjes maar kleine trillende snaartjes. Het idee van Mathur is dat zwarte gaten niets anders zijn dan wazige kluwens van dergelijke snaren – kluwens die zo groot zijn dat ze het gehele gebied binnen de horizon vullen. De Hawkingstraling kan dan omschreven worden als het ‘afbreken’ van kleine stukjes snaar van deze kluwen. Mathur kon vanuit deze aanname aantonen dat de straling van een zwart gat inderdaad vrijwel thermisch is, maar dat er wel degelijk informatie met de straling mee naar buiten komt.

Dezelfde fuzzballs geven ook direct een mogelijk antwoord op onze tweede vraag: wat zijn de microscopische toestanden van zwarte gaten? In Mathurs beeld zijn die microscopische toestanden de verschillende manieren waarop de snaarkluwen ‘opgerold’ kan zijn. Een berekening toont aan dat in eenvoudige gevallen vanuit dit aantal manieren inderdaad de mysterieuze entropie van zwarte gaten verklaard kan worden.

Daarin zijn fuzzballs overigens niet uniek: ook diverse andere benaderingen, vaak direct of indirect gebaseerd op de snaartheorie, leiden in specifieke gevallen tot de juiste entropie. De eersten die een dergelijke benadering ontdekten, waren Andrew Strominger en Cumrun Vafa in 1996. Ook zij reconstrueerden een bepaalde klasse van zwarte gaten in de snaartheorie – in hun geval niet als kluwens van snaren, maar als opeenstapeling van nog hoger dimensionale objecten, de zogeheten D-branes. Ook in hun constructie bleek het tellen van het aantal toestanden de entropie van de betreffende zwarte gaten te reconstrueren.

Afbeelding 7. Cumrun Vafa en Andrew Strominger.Strominger en Vafa gaven als eerste een telargument waarmee de entropie van zwarte gaten verklaard kon worden. Foto’s: Stephanie Mitchell / Harvard University.

Naar boven

En nu?

Daarmee zijn we op het punt aangekomen dat de vraag niet langer is: ‘Hoe verklaren we de informatieparadox en tellen we de toestanden van een zwart gat?’, maar eerder: ‘Hoe weten we welk antwoord het juiste is?’ Voor beide puzzels rond zwarte gaten hebben we inmiddels de nodige puzzelstukjes gevonden die in het antwoord kunnen passen, maar het is niet duidelijk welke stukjes we nodig hebben, welke helemaal niet bij de puzzel horen, en of er misschien nog allerlei stukjes ontbreken. Zet de snaartheorie ons op het juiste spoor, en als dat het geval is, moeten we zwarte gaten dan beschrijven als kluwens van snaren of als opeenstapelingen van D-branes?  Of zijn er bepaalde situaties waarin de ene omschrijving beter is en andere situaties waarin we juist de andere omschrijving nodig hebben? Brengt de oplossing van de informatieparadox met zich mee dat een invallende astronaut een muur van vuur tegenkomt, of ploft die astronaut neer op een kluwen van snaren? Of valt hij toch, zoals in Einsteins oorspronkelijke beeld, zonder iets te merken door de horizon heen?

Traditioneel is het in de natuurkunde zo dat experimenten in dit soort situaties de uitkomst moeten bieden. We willen uiteindelijk immers geen science-fictionwereld beschrijven die zou kunnen bestaan – nee, we willen ons eigen heelal beschrijven, met de natuurwetten die daarin gelden. Als we willen weten of een heliumballon in een versnellende auto naar voren of naar achteren rolt, is de meest overtuigende manier om tot het antwoord te komen om het experiment te doen. We zouden dus het liefst naar hartelust experimenteren met zwarte gaten, maar bij gebrek aan zwarte gaten in het laboratorium (of in de buurt van het zonnestelsel) is dat vooralsnog erg lastig. Daar komt nog eens bij dat het vrijwel onmogelijk is om informatie uit het binnenste van een zwart gat te achterhalen, zelfs als de oplossing van de informatieparadox blijkt te zijn dat die informatie uiteindelijk wel naar buiten komt. Potentiële experimenten zullen zich dus vooral zullen moeten richten op wat er in de buurt van het zwarte gat gebeurt.

Dat maakt de situatie niet volkomen hopeloos. Natuurkundigen zijn erg vindingrijk, dus het valt niet uit te sluiten dat er uiteindelijk een experiment of waarneming wordt bedacht waaruit kan blijken of een zwart gat is opgebouwd uit snaren of uit D-branes. Vooralsnog lijkt het er echter niet op dat een dergelijk experiment of een dergelijk waarneemprogramma binnen afzienbare tijd voorgesteld zal worden. Tot het zover is, zullen we de oplossingen dus moeten zoeken waar ze de afgelopen tientallen jaren gezocht zijn: in de theorie.

Welke stappen kan de theorie nog maken? Allereerst die van veralgemenisering. Vooralsnog is het zo dat de bestaande ideeën over zwarte gaten in vrijwel alle gevallen alleen zijn toegepast op bepaalde klasses van zwarte gaten. Houden de ideeën van Strominger en Vafa stand als we ze toepassen op veel algemenere, niet supersymmetrische zwarte gaten? Kunnen we met fuzzballs ook geladen, draaiende zwarte gaten in ons eigen vierdimensionale heelal beschrijven? Zulke verdere algemenisering kan dienen als selectiemechanisme. Als één idee niet veralgemeniseerd kan worden en een ander wel, wordt het tweede idee daarmee natuurlijk veel aantrekkelijker. Ook kan bij veralgemenisering blijken dat twee ideeën eigenlijk equivalent aan elkaar zijn, en dus in feite verschillende manieren om één wiskundige oplossing te beschrijven.

Naast veralgemenisering is een belangrijke benadering op dit moment het beter begrijpen van de fundamenten. Zwarte gaten zijn met name moeilijk te begrijpen omdat we nog geen volledig coherent beeld hebben van hoe de quantummechanica en de relativiteitstheorie gecombineerd moeten worden. De snaartheorie lijkt hierin een heel eind op weg, maar die theorie is nog allesbehalve compleet en algemeen geaccepteerd. Een eerste doel kan dus zijn om de quantumzwaartekracht zelf beter te begrijpen, om de geleerde lessen vervolgens toe te passen op zwarte gaten. Veel onderzoekers volgen momenteel deze richting. Het verder ontwikkelen van de theorie rond quantuminformatie – die ook gebruikt wordt voor quantumcomputers – zou hierin wel eens een belangrijke rol kunnen spelen, aangezien juist het begrip informatie zo centraal staat – zowel in het oplossen van de informatieparadox als in het begrijpen hoe de verschillende toestanden van een zwart gat op microscopisch niveau de entropie ‘coderen’.

Afbeelding 8. De puzzel van de zwarte gaten.Welke stukjes van de oplossing hebben we al, en welke ontbreken nog? En welke ontbrekende stukjes kan de theorie leveren, en welke het experiment? Afbeelding: Wikipedia-gebruiker Amada44.

Uitspraken over welke aanpak uiteindelijk tot de antwoorden op de bovenstaande vragen zal leiden, zijn natuurlijk niet meer dan koffiedikkijken. Ook over de tijdsduur valt weinig te zeggen: wellicht bereikt iemand morgen al een cruciale doorbraak, maar het is ook beslist niet uitgesloten dat het vinden van de volledige waarheid rond zwarte gaten een proces van nog eens vele tientallen jaren – of zelfs veel langer – zal zijn.

We sluiten dit dossier daarom af met de mededeling dat we het niet afsluiten. Er zullen in de komende jaren ongetwijfeld verdere ideeën over zwarte gaten ontwikkeld worden, en mogelijk ook bestaande ideeën onderuitgehaald. Zodra er iets nieuws te melden valt, zullen we dat in nieuwe aanvullingen op dit dossier laten weten!

Naar boven

Hiermee is het dossier over zwarte gaten – zoals gezegd: voorlopig – beëindigd. Op dinsdag 4 augustus start er een nieuw dossier op de Quantum Universe-site: over snaren en het holgrafisch principe.