De meeste problemen in de natuurkunde zijn moeilijk. Soms is iets gewoon veel werk, zoals het berekenen van de afbuiging van licht in Einsteins algemene relativiteitstheorie, maar kan je met pen en papier en wat goede moed een eind komen. Soms is het echt te veel werk om een probleem met de hand op te lossen, maar kan het door computers heel goed gesimuleerd worden. Zo kan bijvoorbeeld onderzocht worden hoe een brug op zware stormwinden zal reageren.
Een misschien nog wel interessantere klasse van problemen zijn de problemen die je écht niet op kan lossen. Van sommige problemen kun je bewijzen dat ze niet oplosbaar zijn. Hoe werkt dat? En wat heeft het met twee planeten te maken?
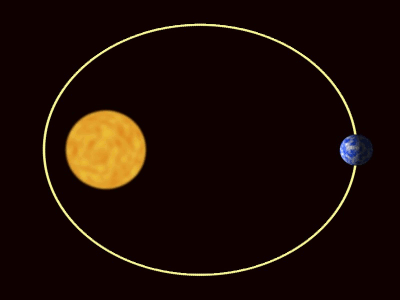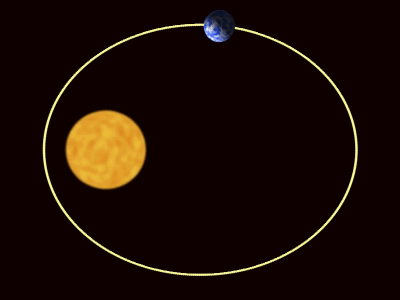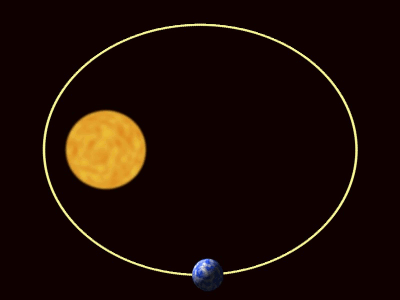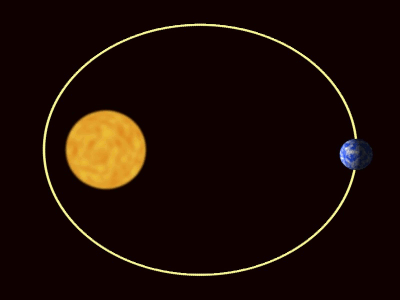
Afbeelding 1:
Ellipsbaan van een planeet om de zon (bron: Wikimedia Commons)
Het bepalen van de baan van planeten om de zon is misschien wel een van de belangrijkste problemen in de geschiedenis van de natuurkunde. Via Tycho Brahe, Johannes Kepler en Isaac Newton leerden we onze plaats in het zonnestelsel. Met zijn differentiaalrekening ontwikkelde Newton zelfs een heel nieuw deel van de wiskunde om dit probleem op te lossen. Sinds Newton blijft het logische volgende probleem echter onopgelost: we weten niet hoe de baan van twee planeten om de zon eruit ziet! Dat wil zeggen: als we ook de zwaartekracht tussen de planeten onderling mee willen nemen in onze berekeningen, wordt het probleem in een klap onoplosbaar. Omdat het de beweging van drie hemellichamen betreft (de zon en twee planeten), wordt dit ook wel het drielichamenprobleem genoemd.
Ook buiten de kringen van Newton en zijn opvolgers bleef dit probleem tot de verbeelding spreken. In Nederland worden wetenschappers tegenwoordig van belastinggeld betaald, maar dit was langere tijd heel anders geregeld. Rijke landheren, hertogen en koningen met een passie voor wetenschap speelden een belangrijke rol in het financieren van het onderzoek. Zo ook Oscar de Tweede, koning van Zweden en Noorwegen. Aan het eind van de negentiende eeuw loofde hij een prijs uit voor de oplossing van het drielichamenprobleem.

Afbeelding II:Koning Oscar II van Zweden en Noorwegen (bron: Wikimedia Commons)
De vergelijkingen van dit probleem komen uit dezelfde theorie die Newton ontwikkeld had om de baan van een enkele planeet om de zon te vinden. De wetenschap was er al die tijd niet achter gekomen hoe Newtons resultaat veralgemeniseerd kon worden. In januari 1889 ging de prijs van de koning naar de Franse wis- en natuurkundige Henri Poincaré. Hij had het probleem echter niet opgelost, maar ontdekte dat het nog veel moeilijker was dan dat men tot dan toe gedacht had!

Afbeelding 3:Henri Poincaré (bron: Wikimedia Commons)
Om dit te begrijpen moeten we nadenken over wat wél een oplossing van het drielichamenprobleem zou zijn. We moeten de drie planeten op een bepaalde plek in het heelal neerzetten. Gegeven dat de wetten van Newton gelden, willen we weten hoe de planeten vanaf die positie verder bewegen. Om te weten waar de maan over een paar uur aan de hemel staat, moeten we eerst weten wat op dit moment de positie van de aarde en de maan is.
Meestal maakt het niet zo heel veel uit wat de beginposities precies zijn. Als de maan een klein stukje verder aan de hemel staat, is zijn baan nog steeds ongeveer hetzelfde. Poincaré kwam erachter dat een typische oplossing van het drielichamenprobleem echter extreem gevoelig is voor deze beginvoorwaardes. Poincaré had bijzondere oplossingen gevonden, maar kwam erachter dat als hij de beginpositie van één van de planeten een klein beetje veranderde, er een radicaal andere beweging volgt!
Deze verrassende conclusie leidt ertoe dat systemen zoals de beweging van drie hemellichamen chaotisch genoemd wordt. Poincaré kwam tot deze ontdekking toen hij de prijs al gewonnen had, en om de verspreiding van zijn manuscript tegen te houden betaalde hij de drukkosten en de correctie van zijn prijsgeld. Net als Newton vond hij echter een nieuw gebied van de wiskunde uit: de chaostheorie.

Afbeelding 4:Chaotisch weer (bron: Pixabay)
Chaotisch gedrag komt ook op andere plekken in de natuur voor. Het verklaart onder andere waarom het zo lastig te voorspellen is of het over drie weken gaat regenen. Het weer is een gevolg is van een complex systeem van wind- en waterbewegingen, en de kleinste meetfout in de windrichting van vandaag kan een enorm effect hebben op de voorspelde hoeveelheid regen over drie weken.
Het blijkt echter met veel computerkracht wel degelijk mogelijk te zijn om oplossingen van het drielichamenprobleem te vinden die bijzonder stabiel zijn. Als planeten eenmaal in precies zo’n configuratie zijn, kunnen ze lange tijd op ongeveer dezelfde manier om elkaar heen bewegen. Chinese onderzoekers hebben nu maar liefst zeshonderd oplossingen gevonden, zoals deze. Wie weet is er ergens in onze Melkweg wel een zonnestelsel dat er zo uit ziet!