Scalairen en vectoren
Om te begrijpen wat tensoren zijn, is het handig om eerst te weten wat scalairen en vectoren zijn. Een scalair is in feite gewoon een getal, bijvoorbeeld het getal 3; het heeft wel een grootte maar geen richting. Voorbeelden van scalaire grootheden in de natuurkunde zijn bijvoorbeeld energie en temperatuur.
Een vector is een grootheid die zowel een grootte als een richting heeft. Mathematisch geven we een tweedimensionale vector weer als
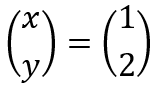
We zien dat aan iedere richting (x en y) een grootte wordt toegekend. Grafisch kunnen we een vector weergeven als een pijl die in een bepaalde richting wijst. De vector hierboven kunnen we dan weergeven als in afbeelding 1: we gaan 1 hokje opzij, en 2 hokjes omhoog.
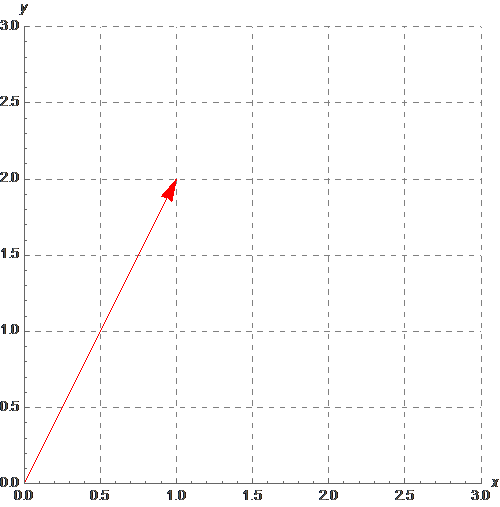
Afbeelding 1: Grafische weergave van een tweedimensionale vector.
In de natuurkunde worden bijvoorbeeld krachten, posities en snelheden weergegeven door vectoren. Een positie met een vector weergeven lijkt erg op schaken: daar wordt de ene as met letters gelabeld en de andere met cijfers. Het paard op D2 zetten zou in vectortaal overeenkomen met de vector
![]()
Als we een snelheid weergeven met dezelfde vector betekent dat dat we met een snelheid van 4 km/uur in de x-richting voortbewegen en met een snelheid van 2 km/uur in de y-richting.
Een kortere manier om vectoren te noteren die in de natuurkunde veel wordt gebruikt, is,
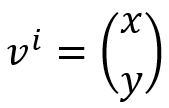
Het superscript kan in dit geval twee waarden aannemen, i = 1 of i = 2, en het labelt in feite de componenten van de vector: v1 = x en v2 = y.
Als we een systeem in drie dimensies willen bekijken, worden de vectoren ook driedimensionaal. Een driedimensionale vector is dus
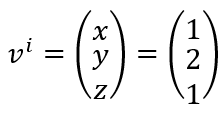
Deze grootheid bedraagt een waarde van 1 in de x-richting, v1 = 1; van 2 in de y-richting, v2 = 2; en van 1 in de z-richting, v3 = 1. Misschien heb je het verband tussen de verschillende dimensies al ontdekt: het komt simpelweg neer op een nieuwe rij aan de vector toevoegen. Zo bekeken is een scalair een eendimensionale vector.
Tensoren
De dimensie van een vector kunnen we dus groter maken door een rij aan de vector toe voegen. Je zou ook een nieuwe kolom toe kunnen voegen, bijvoorbeeld
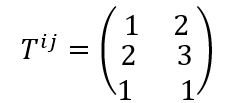
Dit herken je misschien als een matrix (dat is het ook), maar het is ook – na scalairen en vectoren – het makkelijkste voorbeeld van een tensor: het is een tweedimensionale rij van getallen. Het tweedimensionale duidt nu niet op een fysische tweedimensionaliteit (lengte en breedte in de fysieke ruimte), zoals het aantal rijen dat bij een vector wel deed, maar op het feit dat er zich getallen in twee richtingen uitstrekken. Dit is tevens te zien aan het feit dat er nu twee superscripts zijn: en . Het superscript labelt nog steeds de rij, en het nieuwe superscript labelt de kolom. Met behulp van de superscripts kunnen de tensorcomponenten worden aangeduid; zo zien we dat T11 = 1, T12 = 2 en T32 = 1.
Tensoren zijn dus niets meer dan generalisaties van begrippen als scalairen, vectoren enmatrices: het zijn meerdimensionale getallenrijen. Een driedimensionale tensor, Tijk, heeft dus niet alleen rijen en kolommen, maar ook nog een getallenrij die het beeldscherm uitkomt. Hogerdimensionale getallenrijen zijn moeilijk voor te stellen, maar worden desondanks veel gebruikt in de natuurkunde – bijvoorbeeld dus bij het bestuderen van veeldeeltjessystemen.
Tensorcontracties
Om de grafische weergave van tensoren en tensor-netwerken te kunnen behandelen, is het van belang eerst tensorcontracties te begrijpen. We beperken ons voor het gemak tot tweedimensionale getallenrijen. Stel dat we de volgende twee tensoren hebben:
![]()
Hiermee kunnen we een tensorcontractie uitvoeren. We laten eerst zien hoe dat in zijn werk gaat en leggen daarna uit wat er gebeurt:
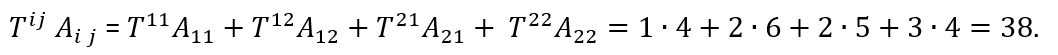
De notatie ‘Tij Aij‘, waarin de indices van T en A hetzelfde zijn, betekent dat we ‘sommeren’ over i en j. Beide indices kunnen de waardes 1 en 2 aannemen; we krijgen dus vier termen. Dit heet de Einstein sommatie conventie. Daarmee is Tij Aij dus een korte notatie voor
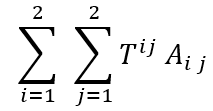
In de theoretische natuurkunde hebben we echter met elkaar hebben afgesproken dat we de sommatietekens niet opschrijven: het simpelweg ‘herhalen’ van een index is voldoende. In het voorbeeld hierboven doen we dat twee keer. Om over de -index te sommeren zetten we eerst i = 1. Dan reduceert de tensorcontractie tot T1jA1j. De Einstein sommatieconventie gebiedt ons nu om te sommeren over de j-index. Dat brengt ons tot:
![]()
Vervolgens zetten we i = 2 en vinden we op eenzelfde manier
![]()
Deze termen nu bij elkaar optellen geeft ons de totale Tij Aij. Nu is het een kwestie van de componenten die bijvoorbeeld T11 en A11 aangeven in te vullen; dat geeft ons uiteindelijk het eindantwoord: 38.
Grafische weergave van tensoren en tensor-netwerken
Tensor-netwerken zijn contracties zoals we net zagen, maar dan van veel tensoren achter elkaar. Omdat het een beetje veel werk wordt om alle termen op te schrijven, is er een manier bedacht om dit grafisch weer te geven. Een voorbeeld hiervan zie je in afbeelding 2.
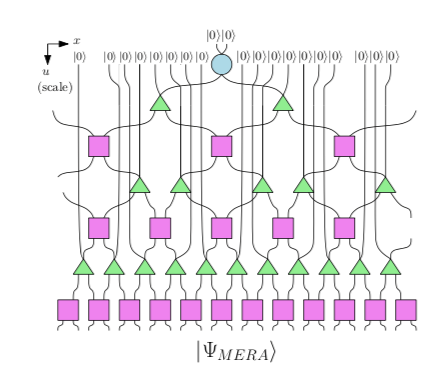
Afbeelding 2: Een tensor-netwerk.De roze vierkanten en de groene driehoeken geven elk een andere tensor weer. De verbindingen tussen de geometrische objecten laten zien dat er gesommeerd wordt over bepaalde indices.
Deze grafische weergave werkt goed, omdat we tensoren zelf grafisch weer kunnen geven: elke verschillende tensor noteren we met een ander geometrisch object. We zouden de tensor Tij bijvoorbeeld kunnen aanduiden met een geel rondje en Akl met een rode ruit. Het aantal indices van de tensoren bepaalt hoeveel ‘poten’ er uit het geometrisch object steken. Dus,

De linkerpoot van het gele rondje geeft de index i aan, en de rechterpoot de index j. Evenzo geeft de linkerpoot van de rode ruit de index k aan en de rechterpoot de index l.
Wellicht is het je opgevallen dat in het tensor-netwerk in afbeelding 2 de poten van roze vierkanten en groene driehoeken veelal verbonden zijn. Dat komt omdat er tussen die tensoren contractie plaatsvindt. In ons eenvoudige voorbeeld met de tensoren Tij en Akl, zouden we bijvoorbeeld hebben

We zien dat de poot die contraheert, de j-index, de twee geometrische objecten verbindt en dat de ongecontraheerde indices, i en k, als ‘bungelende’ poten zijn. Als we een volledige contractie plaats zouden laten vinden, dan zouden we dat grafisch weer kunnen geven als:
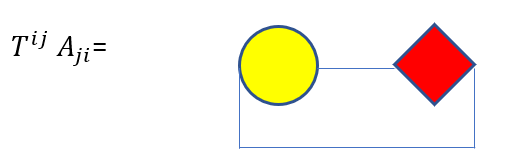
Een wat ingewikkelder voorbeeld van tensorcontracties in grafische weergave is het volgende,
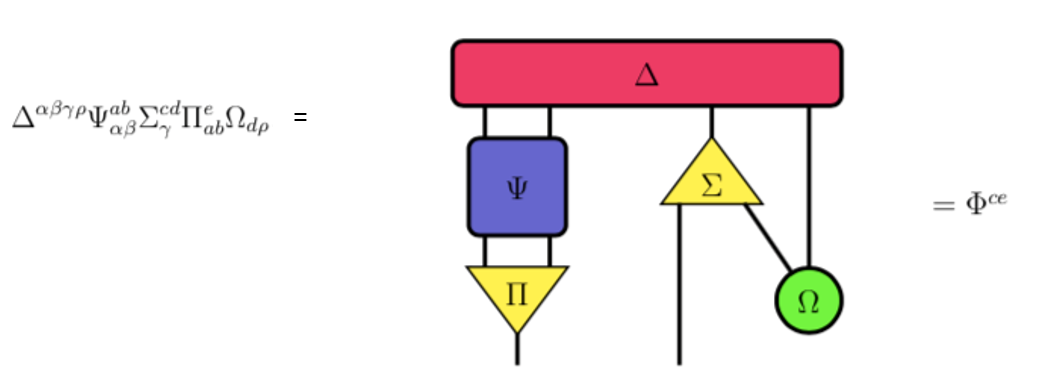
We zien dat de tensor Δαβγδ inderdaad vier poten heeft die verbonden zijn met de tensoren Ψabαβ, Σcdγ en Ωdρ. De verbindingen tussen de tensoren Δ en Ψ gaat via de poten die horen bij de indices α, β; de verbinding tussen Δ en Σ geeft de sommatie over de index γ weer; en de verbinding tussen Δ en Ω komt tot stand door middel van de sommatie over de index ρ. Soortgelijke patronen kunnen we tussen de andere geometrische objecten in dit mininetwerk zien. Bovendien zien we dat in de formule geen sommatie plaatsvindt over de indices c en e: deze letters komen maar één keer in de formule voor. Inderdaad zien we in ons mininetwerk twee bungelende poten, één vanuit de driehoek Π (de index e) en één vanuit de driehoek Σ (de index c).
In de moderne natuurkunde is er een heel vakgebied dat zich met tensor-netwerken bezighoudt. In plaats van twee of vijf tensoren worden er dan soms wel honderden tensoren aan elkaar geplakt, zoals inderdaad in afbeelding 2 te zien is. We noemden al één van de redenen om tensor-netwerken te bestuderen: het beter begrijpen van veeldeeltjesfysica. Met tensornetwerken kunnen we de verschillende deeltjes en hun interacties weergeven. Maar hoe dat precies in zijn werk gaat, daar wijden we later misschien nog eens een stuk aan.